Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-23T12:08:54.039Z Has data issue: false hasContentIssue false
  • English
  • Français

The Pseudo-Orbit Shadowing Property for Markov Operators in the Space of Probability Density Functions

Published online by Cambridge University Press:  20 November 2018

Abraham Boyarsky  and
Pawel Góra
Abraham Boyarsky
Affiliation:
Department of Mathematics Loyola Campus, Concordia University, 7141 Sherbrooke St. West Montreal, Canada H4B 1R6
Pawel Góra
Affiliation:
Department of Mathematics Warsaw University, Warsaw, Poland
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be a space with two metrics d1 and d2. Let S :(X, d1) → (X, d2) be continuous. We say S has the generalized pseudoorbit shadowing property with respect to the metrics d1 and d2 if for every 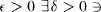every δ-pseudo-orbit in d1 can be ∊-shadowed by a true orbit in d2, i.e., if {x0, x1,…} satisfies 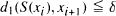for all i ≧ 0, then 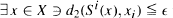for all i ≧ 0. The main result of this note shows that certain Markov operators P : L1→ L1 have the generalized shadowing property on weakly compact subsets of the space of probability density functions, where d1 is the metric of norm convergence and d2 is the metric of weak convergence. An important class of such operators are the Frobenius-Perron operators induced by certain expanding and nonexpanding maps on the interval. When there is exponential convergence of the iterates to the density, we can express δ in terms of ∊. We also show that, unlike the situation in the space X itself, the generalized shadowing property is valid for all parameters in families of maps and that there is stability of the shadowing property.

Keywords

58F1128D05
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 42 , Issue 6 , 01 December 1990 , pp. 1000 - 1017
Copyright
Copyright © Canadian Mathematical Society 1990

Footnotes

This research was supported by a grant from NSERC.

References

1. Bowen, R., On axiom A diffeomorphisms, CBMS Regional Conference Series in Math., No. 35, 1978.Google Scholar
2. Coven, E.M., Kan, I., and Yorke, J.A., Pseudo-orbit shadowing in the family of tent maps, preprint 1986.Google Scholar
3. Lasota, A. and Mackey, M.C., Probabilistic properties and deterministic systems, ambridge University Press, 1985.10.1017/CBO9780511897474CrossRefGoogle Scholar
4. Bauer, W. and Sigmund, K., Topological dynamics of transformations induced in the space of probability measures, Monatsh fur Math., 79, 81-92, 1975.Google Scholar
5. Komuro, M., The pseudo orbit tracing properties in the space of probability measures, Tokyo J. Math., Vol. 72, No. 2, 461-468, 1984.Google Scholar
6. Milnor, J., On the concept of attractor: correction and remarks. Comm. Math. Phys. 102, 517- 519, 1985.Google Scholar
7. Lasota, A. and Yorke, J.A., On the existence of invariant measures for piecewise monotonie transformations, Trans. Amer. Math. Soc., V.116, 481-488, 1973.Google Scholar
8. Komornik, J., Asymptotic periodicity of the interates of weakly constrictive Markov operators , Tohoku Math. Journ. 38, 15-27, 1986.Google Scholar
9. Keller, G., Stochastic stability in some chaotic dynamical systems, Monatsh. fur Math. 94, 313- 333, 1983.Google Scholar
10. Keller, G. (personal communication).Google Scholar
11. Hofbauer, F. and Keller, G., Ergodic properties of invariant measures for piecewise monotonie transformations, Math. Z. 180, 119-140, 1982.Google Scholar
12. Ionescu Tulcea, C. T., and Marinescu, G., Theotie ergodique pour les classes d'opérations non complètement continues. Ann. Math. 52, 140-147, 1950.Google Scholar
13. Lasota, A., Li, T.Y. and Yorke, J.A., Asymptotic periodicity of the iterates of Markov operators, Trans. Amer. Math. Soc, 286, 751-764, 1984.Google Scholar
14. Pelikan, S., Invariant densities for random maps of the interval, Trans. Amer. Math. Soc, 281, 813-825, 1984.Google Scholar
15. Boyarsky, A., Uniqueness of invariant densities for certain random maps of the interval, Can. Math. Bull., Vol. 30 (3), 301-308, 1987.Google Scholar
16. Neveu, J., Mathematical foundations of the calculus of probability, Holden-day, 1965.Google Scholar
17. Szewc, B., The Perron-Frobenius operator in spaces on smooth functions, Erg. Theory and Dyn. Syst., 4, No. 4, 613-643, 1984.Google Scholar
18. Keller, G., Generalized bounded variation and applications to piecewise monotonie transformations, Z.|Wahr. 69, 461-478, 1985.Google Scholar