Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-20T01:48:55.757Z Has data issue: false hasContentIssue false
  • English
  • Français

Pseudo-Measure Energy and Spectral Synthesis

Published online by Cambridge University Press:  20 November 2018

John J. Benedetto
John J. Benedetto*
Affiliation:
University of Maryland, College Park, Maryland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we develop a natural notion of continuous pseudo-measure and study the Stieltjes integral with respect to a given pseudo-measure. The common feature to these two topics is the essential appearance in both of integrals having the form

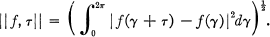
Such integrals come about naturally when one defines the energy of distributions other than measures [6]. The reasons to study continuous pseudo-measures are to find properties analogous with those of continuous measures, and to discover more about the structure of pseudo-measures because of their importance in harmonic analysis, and particularly in spectral synthesis (e.g., [4; 15]). The Stieltjes integral with respect to a pseudo-measure is studied because of its intimate relation with spectral synthesis (e.g., §5); the key observations on this matter were initially made by Beurling [6].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 26 , Issue 4 , August 1974 , pp. 985 - 1001
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Auerbach, H., Sur les dérivées généralées, Fund. Math. 8 (1926), 49–55.Google Scholar
2. Bari, N., Trigonometric series, Volumes I and II (Macmillan, New York, 1964).Google Scholar
3. Benedetto, J., Trigonometric sums associated with pseudo-measures, Ann. Scuola Norm. Sup. Pisa 25 (1971), 229–247.Google Scholar
4. Benedetto, J., Harmonic analysis on totally disconnected sets (Springer Lecture Notes, New York, 1971).Google Scholar
5. Beurling, A., Ensemble exceptionnels, Acta Math. 72 (1940), 1–13.Google Scholar
6. Beurling, A., Analyse spectrale de pseudomesures, C.R. Acad. Sci. Paris Sér. A-B 258 (1964), 406–409, 782-785, 1380-1382, 1984-1987, 2959-1962, 3423-3425.Google Scholar
7. Beurling, A., Construction and analysis of some convolution algebras, Ann. Inst. Fourier (Grenoble) 14 (1964), 1–32.Google Scholar
8. Bray, H. E., Functions of écart fini, Amer. J. Math. 51 (1929), 149–164.Google Scholar
9. Denjoy, A., Sur la definition riemannienne de l'intégrale de Lebesgue, C.R. Acad. Sci. Paris Sér. A-B 193 (1931), 695–698.Google Scholar
10. Goes, G., Uber einige Multiplikatorenklassen, Math. Z. 80 (1963), 324–327.Google Scholar
11. Goldberg, R. R. and Simon, A. B., Characterization of some classes of measures, Acta Sci. Math. (Szeged) 27 (1966), 157–161.Google Scholar
12. Herz, C., The ideal theorem in certain Banach algebras of functions satisfying smoothness conditions, Functional Analysis Symposium at Irvine, 1967.Google Scholar
13. Herz, C., Lipschitz spaces and Bernstein's theorem on absolutely convergent Fourier transforms, J. Math. Mech. 18 (1968), 283–323.Google Scholar
14. Hille, E., On functions of bounded deviation, Proc. London Math. Soc. 31 (1930), 165–173.Google Scholar
15. Kahane, J.-P., Séries de Fourier absolument convergentes (Springer, New York, 1970).Google Scholar
16. Katznelson, Y., Harmonic analysis (Wiley, New York, 1968).Google Scholar
17. Lozinskii, S. M., On a theorem of N. Wiener, Dokl. Akad. Nauk SSSR 49 (1945), 562–565; 53 (1946), 691–694.Google Scholar
18. Neugebauer, C., Symmetric, continuous, and smooth functions, Duke Math J. 31 (1964), 23–32.Google Scholar
19. Neugebauer, C., Smoothness and differentiability in Lp , Studia Math. 25 (1964), 81–91.Google Scholar
20. Stein, E., On limits of sequences of operators, Ann. of Math. 74 (1961), 140–170.Google Scholar
21. Stein, E. and Zymund, A., On the differentiability of functions, Studia Math. 23 (1964), 247–283.Google Scholar
22. Szász, O., Fourier series and mean moduli of continuity. Trans. Amer. Math. Soc. 15 (1937), 366–395.Google Scholar
23. Ul'janov, P. L., Absolute and uniform convergence of Fourier series, Math. USSR-Sb 1 (1967), 169–198.Google Scholar
24. Wiener, N., The quadratic variation of a function and its Fourier coefficients, J. of Math, and Physics 3 (1924), 72–94.Google Scholar
25. Zygmund, A., Trigonometric series, Volumes I and II (Cambridge University Press, Cambridge, 1959).Google Scholar