Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T00:31:38.725Z Has data issue: false hasContentIssue false
  • English
  • Français

Pseudodifferential Resolvent for a Certain Non-Locally-Solvable Operator

Published online by Cambridge University Press:  20 November 2018

C. Hoel
C. Hoel*
Affiliation:
Rutgers University, New Brunswick, New Jersey
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note we construct a pseudo-differential resolvent for 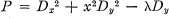by the method of [3] and study the dependence on the parameter λ as λ → 1. Grushin [2] first pointed out that P is solvable and hypoelliptic if λ is not an odd integer, whereas P is neither locally solvable at the origin nor hypoelliptic if λ is an odd integer. Gilioli and Trèves [1] showed that this discrete nature of the condition for solvability persists to a more general class of operators.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 26 , Issue 5 , October 1974 , pp. 1130 - 1140
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Gilioli, A. and Treves, F., An example in the solvability theory of linear PDE's, Amer. J. Math. (to appear).Google Scholar
2. Grushin, V., Les problèmes aux limites dégénères et les operateurs pseudo-differentiels, Actes, Congres Intern. Math., 1970, Tome 2, p. 737 a 743.Google Scholar
3. Hoel, C., Fundamental solutions of some degenerate operators (to appear).Google Scholar
4. Riesz, F. and Sz.-Nagy, B., Functional analysis (F. Ungar Pub. Co., New York, 1955).Google Scholar