Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-20T06:56:11.835Z Has data issue: false hasContentIssue false
  • English
  • Français

Properties of a Class of (0,1)-Matrices Covering a given Matrix

Published online by Cambridge University Press:  20 November 2018

R. P. Anstee
R. P. Anstee*
Affiliation:
University of Waterloo, Waterloo, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

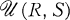We wish to consider the class of (0,1)-matrices with prescribed row and column sums. Let R = (r1, r2, …, rm) and S= (s1, s2, …, sn) be vectors with nonnegative integral entries and r1 + r2 + … + rm = s1 + s2 + … + sn. We define the class to be the set of m × n (0, 1)-matrices with ith row sum ri and jth column sum sj for 1 ≦ i ≦ m and 1 ≦ j ≦ n.

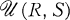Gale and Ryser independently found simple necessary and sufficient conditions for to be nonempty [9 , 14]. From R, we form an m × n (0, 1)-matrix Ā as follows. The ith row sum of Ā is ri and the 1‘s are as far to the left as possible. Let 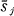be the jth column sum of A. We define the sequence to be the conjugate of the sequence (ri).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 34 , Issue 2 , 01 April 1982 , pp. 438 - 453
Copyright
Copyright © Canadian Mathematical Society 1982

References

1. Anstee, R. P., Ph.D. dissertation, California Institute of Technology, Pasadena, CA. (1980).Google Scholar
2. Bondy, J. A. and U. S. R., Murty, Graph theory with applications (Macmillan, London, 1976).Google Scholar
3. Brualdi, R. A., Matrices of zeros and ones with fixed row and column sum vectors, Letters in Lin. Alg., Lin. Alg. and its Applies. 33 (1980), 159–231.Google Scholar
4. Brualdi, R. A. and Ross, J. A., On Ryser's maximum term rank formula, Lin. Alg. and Its Applies. 29 (1980), 33–38.Google Scholar
5. Ford, L. R., Jr. and Fulkerson, D. R., Flows in networks (Princeton University Press, Princeton, N.J., 1962).Google Scholar
6. Fulkerson, D. R., Hoffman, A. J. and McAndrew, M. H., Some properties of graphs with multiple edges, Can. J. Math. 17 (1965), 166–177.Google Scholar
7. Fulkerson, D. R., Zero-one matrices with zero trace, Pac. J. Math. 10 (1960), 831–836.Google Scholar
8. Fulkerson, D. R., The maximum number of disjoint permutations contained in a matrix of zeros and ones, Can. J. Math. 16 (1964), 729–735.Google Scholar
9. Gale, D., A theorem onflows in networks, Pac. J. Math. 7 (1957), 1073–1082.Google Scholar
10. Kleitman, D. J. and Wang, D. L., Algorithms for constructing graphs and digraphs with given valencies and factors, Discrete Math. 6 (1973), 79–88.Google Scholar
11. Koren, M., Realization of a sum of sequences by a sum graph, Israel J. Math. 15 (1973), 396–403.Google Scholar
12. Kundu, S., The k-factor conjecture is true, Discrete Math. 6 (1973), 367–376.Google Scholar
13. Lovasz, L., Valencies of graphs with 1-factors, Per. Math. Hung. 5 (1974), 149–151.Google Scholar
14. Ryser, H. J., Combinatorial properties of (0,1)-matrices, Can. J. Math. 9 (1957), 371–377.Google Scholar
15. Ryser, H. J., The term rank of a matrix, Can. J. Math. 10 (1958), 57–65.Google Scholar
16. Ryser, H. J., Traces of matrices of zeros and ones, Can. J. Math. 12 (1960), 463–476.Google Scholar
17. Ryser, H. J., Combinatorial mathematics Carus Mathematical Monographs 14 (Math. Assoc, of America, Washington, D.C., 1963).Google Scholar
18. Ryser, H. J., Matrices of zeros and ones in combinatorial mathematics, in: Recent advances in matrix theory (Univ. of Wisconsin Press, Madison, Wise, 1964), 103–124.Google Scholar
19. Ryser, H. J., Combinatorial configurations, SIAM J. Appl. Math. 17 (1969), 593–602.Google Scholar
20. Walkup, D. J., Minimal interchanges of (0,l)-matrices and disjoint circuits in a graph, Can. J. Math. 17 (1965), 831–838.Google Scholar