Hostname: page-component-f554764f5-fnl2l Total loading time: 0 Render date: 2025-04-08T20:36:04.822Z Has data issue: false hasContentIssue false
  • English
  • Français

The Propagation Of a Plane Shock Into a Quiet Atmosphere II

Published online by Cambridge University Press:  20 November 2018

M. H. Martin
M. H. Martin*
Affiliation:
Institute for Fluid Dynamics and Applied Mathematics University of Maryland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. Introduction. In a previous paper (3) the study of one-dimensional, unsteady flows, isentropic or anisentropic, was reduced to the integration of a Monge-Ampère partial differential equation

(1)

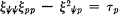
For a polytropic gas, the specific volume

(2) ,

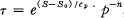takes the form

,

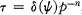once the entropy distribution function S = S(Ψ) is specified.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 7 , 1955 , pp. 284 - 288
Copyright
Copyright © Canadian Mathematical Society 1955

References

1. Chandrasekar, S., On the decay of plane shock waves, Aberdeen Proving Ground, BRL Report No. 423 (1943).Google Scholar
2. Friedrichs, K. O., Formation and decay of shock waves, Comm. on Appl. Math., 1 (1948), 211–245.Google Scholar
3. Martin, M. H., The propagation of a plane shock into a quiet atmosphere, Can. J. Math., 5 (1953), 37–39.Google Scholar