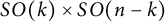Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T18:00:22.542Z Has data issue: false hasContentIssue false
  • English
  • Français

Proof of Laugwitz Conjecture and Landsberg Unicorn Conjecture for Minkowski norms with $SO(k)\times SO(n-k)$-symmetry

Part of: Global differential geometry Local differential geometry General convexity

Published online by Cambridge University Press:  03 June 2021

Ming Xu  and
Vladimir S. Matveev
Ming Xu
Affiliation:
School of Mathematical Sciences, Capital Normal University, Beijing100048, P.R. China e-mail: [email protected]
Vladimir S. Matveev*
Affiliation:
Institut für Mathematik, Fakultät für Mathematik und Informatik, Friedrich-Schiller-Universität Jena, Jena, Germany
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a smooth strongly convex Minkowski norm 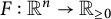$F:\mathbb {R}^n \to \mathbb {R}_{\geq 0}$ , we study isometries of the Hessian metric corresponding to the function 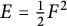$E=\tfrac 12F^2$ . Under the additional assumption that F is invariant with respect to the standard action of 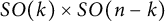$SO(k)\times SO(n-k)$ , we prove a conjecture of Laugwitz stated in 1965. Furthermore, we describe all isometries between such Hessian metrics, and prove Landsberg Unicorn Conjecture for Finsler manifolds of dimension 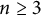$n\ge 3$ such that at every point the corresponding Minkowski norm has a linear 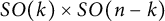$SO(k)\times SO(n-k)$ -symmetry.

Keywords

Minkowski normHessian isometryLaugwitz ConjectureLandsberg Unicorn ConjectureLegendre transformation

MSC classification

Primary: 52A20: Convex sets in $n$ dimensions (including convex hypersurfaces) 53C21: Methods of Riemannian geometry, including PDE methods; curvature restrictions 53C30: Homogeneous manifolds 53B40: Finsler spaces and generalizations (areal metrics)
Type
Article
Information
Canadian Journal of Mathematics , Volume 74 , Issue 5 , October 2022 , pp. 1486 - 1516
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author is supported by Beijing Natural Science Foundation (No. Z180004), NSFC (No. 11771331 and No. 11821101), and Capacity Building for Sci-Tech Innovation—Fundamental Scientific Research Funds (No. KM201910028021). The second author thanks DFG for partial support via projects MA 2565/4 and MA 2565/6.

References

Alvarez Paiva, J., Some problems on Finsler geometry . In: Handbook of differential geometry. Vol. II, Franki J. E. Dillen, Leopold C. A. Verstraelen, (eds.), Elsevier and North-Holland, Amsterdam, Netherlands, 2006, pp. 1–33.Google Scholar
Asanov, G. S., Finsler cases of GF-space. Aequationes Math. 49(1995), no. 3, 234–251.CrossRefGoogle Scholar
Asanov, G. S., Finslerian metric functions over the product  $\mathbb{R}\times M$  and their potential applications . Rep. Math. Phys. 41(1998), no. 1, 117–132.CrossRefGoogle Scholar
Asanov, G. S., Finsleroid–Finsler space with Berwald and Landsberg conditions. Rep. Math. Phys. 58(2006), 275–300.CrossRefGoogle Scholar
Asanov, G. S., Finsleroid–Finsler space with geodesic spray coefficients. Publ. Math. Debrecen. 71(2007), 397–412.Google Scholar
Bao, D., On two curvature-driven problems in Riemann–Finsler geometry . In: Finsler geometry, Sapporo 2005—in memory of Makoto Matsumoto, S.V. Sabau and H. Shim ada, (eds.), Adv. Stud. Pure Math., 48, Mathematics Society, Tokyo, 2007, pp. 19–71.CrossRefGoogle Scholar
Bao, D., Chern, S. S., and Shen, Z., Rigidity issues on Finsler surfaces. Rev. Roumaine Math. Pures Appl. 42(1997), 707–735.Google Scholar
Bao, D., Chern, S. S., and Shen, Z., An introduction to Riemann–Finsler geometry. Graduate Texts in Mathematics, 200, Springer, New York, 2000.CrossRefGoogle Scholar
Berwald, L., Ueber Finslersche und Cartansche Geometrie. I. Geometrische Erklärungen der Krümmung und des Hauptskalars eines zweidimensionalen Finslerschen Raumes (in German). Mathematica 17(1941), 34–58.Google Scholar
Berwald, L., Ueber Finslersche und Cartansche Geometrie. IV. Projektivkrümmung allgemeiner affiner Räume und Finslersche Räume skalarer Krümmung. Ann. Math. (2) 48(1947), 755–781.Google Scholar
Bliss, G. A., A generalization of the notion of angle. Trans. Amer. Math. Soc. 7(1906), no. 2, 184–196.CrossRefGoogle Scholar
Bolsinov, A. V., Konyaev, A. Y., Matveev, V. S., Applications of Nijenhuis geometry II: maximal pencils of multihamiltonian structures of hydrodynamic type. Nonlinearity 34 (8)(2021):5136–5162.CrossRefGoogle Scholar
Bolsinov, A. V., Matveev, V. S., and Rosemann, S., Local normal forms for c-projectively equivalent metrics and proof of the Yano–Obata conjecture in arbitrary signature. Proof of the projective Lichnerowicz conjecture for Lorentzian metrics. Annales de l'ENS, in print, 2015. arxiv:1510.00275 Google Scholar
Brickell, F., A theorem on homogeneous functions. J. Lond. Math. Soc. 42(1967), 325–329.CrossRefGoogle Scholar
Cartan, É., Sur les espaces de Finsler. C. R. Acad. Sci. Paris. 196(1933), 582–586.Google Scholar
Cheng, S. Y. and Yau, S.-T., The real Monge–Ampere equation and affine flat structures. In: Proceedings of the 1980 Beijing Symposium on Differential Geometry and Differential Equations, Vol. 1, 2, 3 (Beijing, 1980), Sci. Press Beijing, Beijing, 1982, pp. 339–370.Google Scholar
Chern, S.-S. and Shen, Z., Riemann–Finsler geometry, Nankai tracts in mathematics. Vol. 6. World Scientific, Singapore, 2005.CrossRefGoogle Scholar
Crampin, M., On Landsberg spaces and the Landsberg–Berwald problem. Houston J. Undergrad. Math. 37(2011), no. 4, 1103–1124.Google Scholar
Crampin, M., Finsler spaces of $\left(\alpha, \beta \right)$ type and semi-C-reducibility. Publ. Math. Debrecen. 98(2021), no. 3–4, 419–454.Google Scholar
Deng, S. and Xu, M., Left invariant Clifford–Wolf homogeneous  $\left(\alpha, \beta \right)$ -metrics on compact semisimple Lie groups . Transform. Groups 20(2015), no. 2, 395–416.CrossRefGoogle Scholar
Deng, S. and Xu, M., (α1,α2)-metrics and Clifford–Wolf homogeneity . J. Geom. Anal. 26(2016), 2282–2321.CrossRefGoogle Scholar
Dodson, C., A short review on Landsberg spaces. In: Workshop on Finsler and Semi-Riemannian Geometry, San Luis Potosi, Mexico, 2006, pp. 24–26.Google Scholar
Eschenburg, J.-H. and Heintze, E., Unique decomposition of Riemannian manifolds. Proc. Amer. Math. Soc. 126(1998), no. 10, 3075–3078.Google Scholar
Feng, H., Han, Y., and Li, M., An equivalence theorem for a class of Minkowski spaces and applications. Sci. China Math. 64(2021), 1429–1446. https://doi.org/10.1007/s11425-020-1812-3 CrossRefGoogle Scholar
Gelfand, I. M. and Ja, I., Dorfman, Hamiltonian operators and algebraic structures associated with them (in Russian). Funktsional. Anal. i Prilozhen. 13(1979), no. 4, 13–30.Google Scholar
Hamel, G., Über die Geometrien, in denen die Geraden die Kürzesten sind (in German). Math. Ann. 57(1903), no. 2, 231–264.CrossRefGoogle Scholar
Helgason, S., Differential geometry, lie groups, and symmetric spaces. Academic Press, San Diago, 1978.Google Scholar
Ishihara, S., Homogeneous Riemannian spaces of four dimensions. J. Math. Soc. Japan 7(1955), 345–370.CrossRefGoogle Scholar
Ji, M. and Shen, Z., On strongly convex indicatrices in Minkowski geometry. Canad. Math. Bull. 45(2002), no. 2, 232–246.CrossRefGoogle Scholar
Kozma, L., On holonomy groups of Landsberg manifolds. Tensor (N.S.) 62(2000), 87–90.Google Scholar
Landsberg, G., Über die Krümmung in der Variationsrechnung. Math. Ann. 65(1908), 313–349.CrossRefGoogle Scholar
Laugwitz, D., Differentialgeometrie in Vektorräumen, unter besonderer Berücksichtigung der unendlichdimensionalen Räume. Braunschweig, Germany, 1965.Google Scholar
Li, A. M., Simon, U., Zhao, G. S., and Hu, Z. J., Global affine differential geometry of hypersurfaces . De Gruyter expositions in mathematics, Vol. 11. A.-M. Li, U. Simon, G. Zhao and Z. Hu, (eds.), Walter de Gruyter & Co., Berlin, 1993.Google Scholar
Matsumoto, M., On Finsler spaces with Randers metric and special forms of important tensors. J. Math. Kyoto Univ. 14(1974), 477–498.Google Scholar
Matsumoto, M., Remarks on Berwald and Landsberg spaces . In: Finsler geometry (Seattle, WA, 1995), Contemporary Mathematics, 196, American Mathematical Society, Providence, RI, 1996, pp. 79–82.CrossRefGoogle Scholar
Matsumoto, M. and Shibata, C., On semi-C-reducibility, T-tensor $=0$ , and S4-likeness of Finsler spaces . J. Math. Kyoto Univ. 19(1979), no. 2, 301–314.Google Scholar
Matveev, V. S., On “All regular Landsberg metrics are always Berwald” by Z. I. Szabo. Balkan J. Geom. 14(2009), 50–52.Google Scholar
Matveev, V. S. and Troyanov, M., The Binet–Legendre metric in Finsler geometry. Geom. Topol. 16(2012), 2135–2170.CrossRefGoogle Scholar
Mo, X. and Zhou, L., The curvatures of spherically symmetric Finsler metrics in ℝn . Preprint, 2014. arxiv:1202.4543 Google Scholar
Obata, M., On n-dimensional homogeneous spaces of Lie groups of dimension greater than n(n − 1) / 2 . J. Math. Soc. Japan 7(1955), 371–388.CrossRefGoogle Scholar
Rund, H., The differential geometry of Finsler spaces . Die Grundlehren der Mathematischen Wissenschaften. Vol. 101, Springer, Berlin, Göttingen, and Heidelberg, 1959.Google Scholar
Schneider, R., Über die Finslerräume mit  ${S}_{ijkl}=0$  (in German) . Arch. Math. (Basel) 19(1968), 656–658.CrossRefGoogle Scholar
Schneider, R., Convex bodies: The Brunn–Minkowski theory. 2nd ed. Cambridge University Press, Cambridge, MA, 2013.Google Scholar
Shen, Z., Lectures on Finsler geometry. World Scientific, Singapore, 2001.Google Scholar
Shen, Z., Some open problems in Finsler geometry. 2009. https://www.math.iupui.edu/~zshen/Research/papers/Problem.pdf Google Scholar
Shen, Z., On a class of Landsberg metrics in Finsler geometry. Canad. J. Math. 61(2009), 1357–1374.CrossRefGoogle Scholar
Shima, H., The geometry of Hessian structures. World Scientific, Singapore, 2007.CrossRefGoogle Scholar
Shima, H., Geometry of Hessian structures . In: Nielsen, F. and Barbaresco, F. (eds.), Geometric science of information, Lecture Notes in Comput. Sci., 8085, Springer, Heidelberg, Germany, 2013, pp. 37–55.CrossRefGoogle Scholar
Szabó, Z. I., Positive definite Berwald spaces (structure theorems). Tensor (N. S.) 35(1981), 25–39.Google Scholar
Xu, M. and Deng, S., The Landsberg equation of a Finsler space. Ann. Sc. Norm. Super. Pisa Cl. Sci. XXII(2021), 31–51. https://doi.org/10.2422/2036-2145.201809_015 Google Scholar
Yano, K., On n-dimensional Riemannian spaces admitting a group of motions of order n(n − 1) / 2 + 1. Trans. Amer. Math. Soc. 74(1953), 260–279.Google Scholar
Zhou, S., Wang, J., and Li, B., On a class of almost regular Landsberg metrics. Sci. China Math. 62(2019), no. 5, 935–960.CrossRefGoogle Scholar