Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T15:13:39.179Z Has data issue: false hasContentIssue false
  • English
  • Français

Projectors on the Generalized Eigenspaces for Neutral Functional Differential Equations in Lp Spaces

Part of: General theory of linear operators Nonlinear operators and their properties Functional-differential and differential-difference equations Parabolic equations and systems

Published online by Cambridge University Press:  20 November 2018

Arnaud Ducrot ,
Zhihua Liu  and
Pierre Magal
Arnaud Ducrot
Affiliation:
UMR CNRS 5251 IMB and INRIA Bordeaux sud-ouest Anubis, Université de Bordeaux, 33000 Bordeaux, France, e-mail: [email protected], [email protected]
Zhihua Liu
Affiliation:
(Liu) Department of Mathematics, Beijing Normal University, Beijing 100875, PR China e-mail: [email protected]
Pierre Magal
Affiliation:
(Liu) Department of Mathematics, Beijing Normal University, Beijing 100875, PR China e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We present the explicit formulas for the projectors on the generalized eigenspaces associated with some eigenvalues for linear neutral functional differential equations 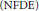$\left( \text{NFDE} \right)$ in 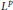${{L}^{p}}$ spaces by using integrated semigroup theory. The analysis is based on the main result established elsewhere by the authors and results by Magal and Ruan on non-densely defined Cauchy problem. We formulate the 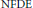$\text{NFDE}$ as a non-densely defined Cauchy problem and obtain some spectral properties from which we then derive explicit formulas for the projectors on the generalized eigenspaces associated with some eigenvalues. Such explicit formulas are important in studying bifurcations in some semi-linear problems.

Keywords

neutral functional differential equationssemi-linear problemintegrated semigroupspectrumprojectors

MSC classification

Secondary: 34K05: General theory 35K57: Reaction-diffusion equations 47A56: Functions whose values are linear operators (operator and matrix valued functions, etc., including analytic and meromorphic ones) 47H20: Semigroups of nonlinear operators
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 62 , Issue 1 , 01 February 2010 , pp. 74 - 93
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] M., Adimy and K., Ezzinbi, A class of linear partial neutral functional-differential equations with nondense domain. J. Differential Equations 147(1998), no. 2, 285-332. doi:10.1006/jdeq.1998.3446Google Scholar
[2] A., Batkai and S., Piazzera, Semigroups and linear partial differential equation with delay. J. Math. Anal. Appl. 264(2001), no. 1, 1-20. doi:10.1006/jmaa.2001.6705Google Scholar
[3] F. E., Browder, On the spectral theory of elliptic differential operators. I. Math. Ann. 142(1960/1961), 22-130. doi:10.1007/BF01343363Google Scholar
[4] O., Diekmann, S. A., van Gils, S. M., Verduyn Lunel, and Walther, H.-O., Functional, Complex, and Nonlinear Analysis. Applied Mathematical Sciences 110, Springer-Verlag, New York, 1995.Google Scholar
[5] A., Ducrot, Z., Liu, and P., Magal, Essential growth rate for bounded linear perturbation of non-densely defined Cauchy problems. J. Math. Anal. Appl. (341)(2008), no. 1, 501-518. doi:10.1016/j.jmaa.2007.09.074Google Scholar
[6] Engel, K.-J. and R., Nagel, One-Parameter Semigroups for Linear Evolution Equations. Graduate Texts in Mathematics 194, Springer-Verlag, New York, 2000.Google Scholar
[7] J. K., Hale, Functional Differential Equations. Applied Mathematical Sciences 3, Springer-Verlag, New York, 1971.Google Scholar
[8] J. K., Hale, Theory of Functional Differential Equations Second edition. Applied Mathematical Sciences 3, Springer-Verlag, New York, 1977.Google Scholar
[9] J. K., Hale and S. M., Verduyn Lunel, Introduction to Functional Differential Equations. Applied Mathematical Sciences 99, Springer-Verlag, New York, 1993.Google Scholar
[10] Z., Liu, P., Magal, and S., Ruan, Projectors on the generalized eigenspaces for functional differential equations using integrated semigroup. J. Differential Equations 244(2008), no. 7, 1784-1809. doi:10.1016/j.jde.2008.01.007Google Scholar
[11] P., Magal and S., Ruan, On integrated semigroups and age structured models in Lp spaces. Differential Integral Equations 20(2007), no. 2, 197-239.Google Scholar
[12] P., Magal and S., Ruan, Center Manifolds for Semilinear Equations with Non-dense Domain and Applications to Hopf Bifurcation in Age Structured Models, Mem. Amer. Math. Soc. 202(2009), no. 951.Google Scholar
[13] H. R., Thieme, Quasi-compact semigroups via bounded perturbation. In: Advances in Mathematical Population Dynamics—Molecules, Cells and Man. Ser. Math. Biol. Med. 6, World Sci. Publishing, River Edge, NJ, 1997, pp. 691-711.Google Scholar
[14] G. F., Webb, Autonomous nonlinear differential equations and nonlinear semigroups. J. Math. Anal. Appl. 46(1974), 1-12. doi:10.1016/0022-247X()90277-7 Google Scholar
[15] G. F., Webb, Functional-differential equations and nonlinear semigroups in Lp-spaces. J. Differential Equations 92(1976), no. 1, 71-89. doi:10.1016/0022-039690097-8Google Scholar
[16] G. F., Webb, Theory of Nonlinear Age-Dependent Population Dynamics. Monographs and Textbooks in Pure and Applied Mathematics 89, Marcel Dekker, New York, 1985.Google Scholar
[17] G. F., Webb, An operator-theoretic formulation of asynchronous exponential growth. Trans. Amer. Math. Soc. 303(1987), no. 2, 155-164. doi:10.2307/2000695Google Scholar
[18] Wu, J., Theory and Applications of Partial Functional-Differential Equations. Applied Mathematical Sciences 119, Springer-Verlag, New York, 1996.Google Scholar