No CrossRef data available.
Article contents
Projective Homotopy Classes of Stiefel Manifolds
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Given a homotopy class [f] in πn(X), we say that [f] is projective if and only if there is a homotopy commutative factorization
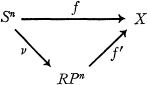
where v is the standard double covering. We then denote by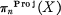 
the subset of projective homotopy classes in πn(X).
The notion of projective homotopy classes was studied in the author's thesis [5], and the projective homotopy classes for spheres in the stable range, up through the 3-stem were calculated in [6].
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1972
References
1.
Mosher, R. E. and Tangora, M. C., Cohomology operations and applications in homotopy theory (Harper and Row, New York, 1966).Google Scholar
2.
Paechter, G. F., The groups πr(Vm,n)(I), Quart. J. Math. Oxford Ser.
7 (1956), 249–268.Google Scholar
4.
Steenrod, N. and Epstein, D. B. A., Cohomology operations, Annals of Mathematics Studies 50 (Princeton University Press, Princeton, 1962).Google Scholar
5.
Strutt, J. R. A., Projective homotopy classes, Ph.D. thesis, University of Illinois, 1970.Google Scholar
6.
Strutt, J. R. A., Projective homotopy classes of spheres in the stable range (to appear in Bol. Soc. Mat. Mex.).Google Scholar
7.
Zvengrowski, P., Skew linear vector fields on spheres, J. London Math. Soc.
3 (1971), 625–632.Google Scholar
You have
Access