Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T15:42:12.646Z Has data issue: false hasContentIssue false
  • English
  • Français

Projective and Multigraded Representations of Monomial and Multisigned Groups I. Graded Representations of a Twisted Product

Published online by Cambridge University Press:  20 November 2018

Peter Hoffman
Peter Hoffman*
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, Ontario, N2L 3G1
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Motivated by the problem of giving a functorial (or at least uniform) description of the projective representations for wreath products Gʅ Snin terms of those for G, we study a certain binary operation 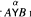on the class of “cyclic covering groups with parities”. Along with setting up the basic machinery associated to representations graded by (Ζ/2)ℓ , the main result is a description of the irreducibles for 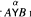in terms of a (tensorlike) product of those for Aand for B.Finally we describe a programme for producing a PSH-algebra theory in this context, analogous to that of Zelevinsky for the case ℓ=0, and that of the author with with Michael Bean (structure) and with John Humphreys (applications) for the case ℓ=1

Keywords

20C2520C1516A2420C30
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 45 , Issue 2 , 01 April 1993 , pp. 295 - 339
Copyright
Copyright © Canadian Mathematical Society 1993

References

[A-B-S] Atiyah, M.F., Bott, R. and Shapiro, A., Clifford modules, Topology (1) 3(1964), 3–38.Google Scholar
[A-T] Atiyah, M.F. and Tall, D.O., Group representations,ƛ-rings, and the J-homomorphism, Topology 8(1969), 253–297.Google Scholar
[B] Bean, M., Unpublished manuscript, 1988.Google Scholar
[B-H] Bean, M. and Hoffman, P.N., Zelevinsky algebras related to projective representations, Trans. Amer. Math. Soc. 309(1988), 99–111.Google Scholar
[D] Dade, E.C., Compounding Clifford's theory, Ann. Math. (2) 91(1970), 236–290.Google Scholar
[H-Hl] Hoffman, P.N. and Humphreys, J.F., Hopf algebras and projective representations ofG\Sn and GlAn, Can. J. Math. 38(1986), 1380–1458.Google Scholar
[H-H2] Hoffman, P.N., Projective representations of generalized symmetric groups using PSH-algebras, Proc. London Math. Soc. (3) 59(1989), 483–506.Google Scholar
[H-H3] Hoffman, P.N., Projective Representations of the Symmetric Groups, Oxford University Press, Oxford, 1992.Google Scholar
[Md] Macdonald, I.G., Symmetric Functions and Hall Polynomials, Oxford University Press, Oxford, 1979.Google Scholar
[Ml] MacLane, S., Homology, Springer-Verlag, New York, 1967.Google Scholar
[Rl] Read, E.W., On the projective characters of the symmetric group, J. London Math. Soc. (2) 15(1977), 456–464.Google Scholar
[R2] Read, E.W., On the Schur multiplier of a wreath product, Illinois J. Math. 20(1976), 456–466.Google Scholar
[S] Schmid, P., Clifford theory of simple modules, Proc. of Symposia in Pure Math. AMS (2) 47(1987), 75–82.Google Scholar
[Z] Zelevinsky, A.V., Representations of Finite Classical Groups—a Hopf Algebra Approach, Lecture Notes in Mathematics 869, Springer-Verlag, Berlin, 1981.Google Scholar