Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-20T14:34:05.917Z Has data issue: false hasContentIssue false
  • English
  • Français

Projections on Bergman Spaces Over Plane Domains

Published online by Cambridge University Press:  20 November 2018

Jacob Burbea
Jacob Burbea*
Affiliation:
University of Pittsburgh, Pittsburgh, Pennsylvania
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let D be a bounded plane domain and let Lp(D) stand for the usual Lebesgue spaces of functions with domain D, relative to the area Lebesque measure dσ(z) = dxdy. The class of all holomorphic functions in D will be denoted by H(D) and we write Bp(D) = Lp(D) ∩ H(D). Bp(D) is called the Bergman p-space and its norm is given by

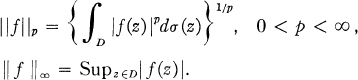
Let 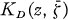be the Bergman kernel of D and consider the Bergman projection

(1.1)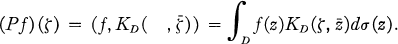

It is well known that P is not bounded on Lp(D), p = 1, ∞, and moreover, it can be shown that there are no bounded projections of L∞(Δ) onto B∞(Δ).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 6 , 01 December 1979 , pp. 1269 - 1280
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Bekollé, D. and Bonami, A., Inégalités à poids pour le noyau de Bergman, C. R. Acad. Se. Paris. 286 (1978), 775–778.Google Scholar
2. Bergman, S. and Schiffer, M., Kernel functions and conformai mapping, Compositio Math. 8 (1951), 205–249.Google Scholar
3. Bers, L., Automorphic forms and Poincaré series for infinitely generated Fuchsian groups, Amer. J. Math. 87 (1965), 196–214.Google Scholar
4. Brennan, J. E., The integrability of the derivative in conformai mapping, J. London Math. Soc. 18 (1978), 261–272.Google Scholar
5. Coifman, R. R. and Fefferman, C., Weighted norm inequalities for maximal functions and singular integrals, Studia Math. 51 (1974), 241–250.Google Scholar
6. Hiibner, O., Die Faktorisierung konformer Abbildungen und Anwendungen, Math. Z. 92 (1966), 95–109.Google Scholar
7. Kellogg, O. D., Harmonic functions and Green1 s integral, Trans. Amer. Math. Soc. 13 (1912), 109–132.Google Scholar
8. Lindenstrauss, J. and Pelczynski, A., Contributions to the theory of the classical Banach spaces, J. Func. Analysis. 8 (1971), 225–249.Google Scholar
9. Pommerenke, Chr., Univalent functions (Vandenhoeck and Ruprecht, Gôttingen, 1975).Google Scholar
10. Stein, E. M., Singular integrals and differentiability properties of functions (Princeton Univ. Press, Princeton, 1970).Google Scholar
11. Stein, E. M., Singular integrals and estimates for the Cauchy-Riemann equations, Bull. Amer. Math. Soc. 79 (1973), 440–445.Google Scholar
12. Tsuji, M., Potential theory in modern function theory (Maruzen Co., Ltd., Tokyo, 1959).Google Scholar
13. Warschawski, S. E., On conformai mapping of regions bounded by smooth curves, Proc. Amer. Math. Soc. 2 (1951), 254–261.Google Scholar
14. Zaharjuta, V. P. and Judovic, V. I., The general form of a linear functional in Hp1, (Russian) Uspehi. Mat. Nauk. 19 (1964), 139–142.Google Scholar