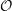 ${\mathcal{O}}$ for the Periplectic Lie Superalgebra
${\mathcal{O}}$ for the Periplectic Lie SuperalgebraPublished online by Cambridge University Press: 16 November 2018
We solve two problems in representation theory for the periplectic Lie superalgebra 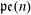 $\mathfrak{p}\mathfrak{e}(n)$, namely, the description of the primitive spectrum in terms of functorial realisations of the braid group and the decomposition of category
$\mathfrak{p}\mathfrak{e}(n)$, namely, the description of the primitive spectrum in terms of functorial realisations of the braid group and the decomposition of category 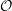 ${\mathcal{O}}$ into indecomposable blocks.
${\mathcal{O}}$ into indecomposable blocks.
To solve the first problem, we establish a new type of equivalence between category 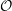 ${\mathcal{O}}$ for all (not just simple or basic) classical Lie superalgebras and a category of Harish-Chandra bimodules. The latter bimodules have a left action of the Lie superalgebra but a right action of the underlying Lie algebra. To solve the second problem, we establish a BGG reciprocity result for the periplectic Lie superalgebra.
${\mathcal{O}}$ for all (not just simple or basic) classical Lie superalgebras and a category of Harish-Chandra bimodules. The latter bimodules have a left action of the Lie superalgebra but a right action of the underlying Lie algebra. To solve the second problem, we establish a BGG reciprocity result for the periplectic Lie superalgebra.
Present address: School of Mathematical Sciences, Xiamen University, Xiamen 361005, China Email: [email protected]
The first author is supported by Vergstiftelsen, and the second author is supported by ARC grant DE170100623.