Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-24T03:37:21.136Z Has data issue: false hasContentIssue false
  • English
  • Français

Power-Rich and Power-Deficient LCA Groups

Published online by Cambridge University Press:  20 November 2018

M. A. Khan
M. A. Khan*
Affiliation:
Kuwait University, Kuwait
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [4], Edwin Hewitt denned a-rich LCA (i.e., locally compact abelian) groups and classified them by their algebraic structure. In this paper, we study LCA groups with some properties related to a-richness. We define an LCA group G to be power-rich if for every open neighbourhood V of the identity in G and for every integer n > 1, λ(nV) > 0, where nV = {nx ∈ G : x ∈ V} and λ is a Haar measure on G. G is power-meagre if for every integer n > 1, there is an open neighbourhood V of the identity, possibly depending on n, such that λ(nV) = 0. G is power-deficient if for every integer n > 1 and for every open neighbourhood V of the identity such that 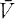is compact, 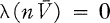. G is dual power-rich if both G and Ĝ are power-rich. We define dual power-meagre and dual power-deficient groups similarly.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 3 , 01 June 1981 , pp. 664 - 670
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Armacost, D. L. and Armacost, W. L., Uniqueness in structural theorems for LCA groups, Can. J. Math. 30 (1978), 593–599.Google Scholar
2. Fuchs, L., Infinité abelian groups, Vol. 1 (Academic Press, New York, 1970).Google Scholar
3. Halmos, P. R., Measure theory (D. Van Nostrand Co., New York, 1950).Google Scholar
4. Hewitt, E., A structural property of certain locally compact abelian groups, Duke Math. J. 32 (1965), 237–238.Google Scholar
5. Hewitt, E. and Ross, K., Abstract harmonic analysis, Vol. 1 (Academic Press, New York, 1963).Google Scholar
6. Moskowitz, M., Homologuai algebra in locally compact abelian groups, Trans. Amer. Math. Soc. 127 (1967), 361–404.Google Scholar