Let 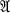denote the set of functions of a complex variable z, regular at z = 0, and let I denote the set of non-negative integers. For f ∈ 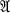put

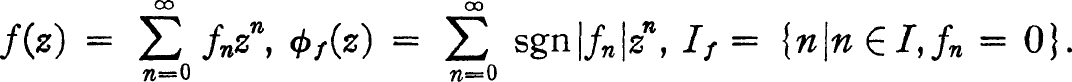
For a given subset 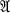0 of 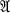there arises the problem of characterizing the admissible gap sets If of functions f in 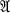0. When 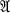0 is the set R of rational functions a complete solution in given by the following theorem:

(A) Let f ∈ R and let If be infinite. Then there exist integers L, L1, L2… , L3 such that 0 ≤ L1 < L2 … < Ls < L, and If = {n|n ∈ I, n ≡ Lj (mod L), j =1, … , s} U I\ where V is a Unite exceptional set.