Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T00:56:56.988Z Has data issue: false hasContentIssue false
  • English
  • Français

Positive Perturbations and Unitary Equivalence

Published online by Cambridge University Press:  20 November 2018

C. R. Putnam
C. R. Putnam*
Affiliation:
Purdue University, West Lafayette, Indiana
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let T be a (not necessarily bounded) self-adjoint operator on a Hilbert space H with the spectral resolution 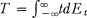The set of elements x in H for which ||Etx||2 is absolutely continuous is a subspace, H a, of H which reduces T. (See H almos [1, p. 104]; Kato [2, p. 516].) If H a ≠ 0, the restriction of T to DT ⋂ H a is called the absolutely continuous part of T; in case H = H a, T is said to be absolutely continuous.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 29 , Issue 1 , 01 February 1977 , pp. 161 - 164
Copyright
Copyright © Canadian Mathematical Society 1977

Footnotes

This work was supported by a National Science Foundation research grant.

References

1. Halmos, P. R., Introduction to Hilbert space and the theory of spectral multiplicity (Chelsea Pub. Co., New York, 1951.Google Scholar
2. Kato, T., Perturbation theory for linear operators, Die Grundlehre der mathematischen Wissenschaften, 132 (Springer, 1966).Google Scholar
3. Putnam, C. R., A note on inverses of differential operators, Math. Zeit. 64 (1956), 149–150.Google Scholar
3. Putnam, C. R. Commutation properties of Hilbert space operators and related topics, Ergebnisse der Math., 36 (Springer, 1967).Google Scholar
5. Stone, M. H., Linear transformations in Hilbert space and their applications to analysis, Amer. Math. Soc. Colloq. Publications, vol. 15, 1932.Google Scholar