Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T00:23:41.119Z Has data issue: false hasContentIssue false
  • English
  • Français

Positive Forms on Nuclear *-Algebras and Their Integral Representations

Published online by Cambridge University Press:  20 November 2018

Alain Bélanger  and
Erik G. F. Thomas
Alain Bélanger
Affiliation:
Department of Mathematics York University North York, Ont. M3J 1P3
Erik G. F. Thomas
Affiliation:
Department of Mathematics University of Groningen, P.O. Box 800, 9700 AV Groningen, TheNetherlands
Rights & Permissions [Opens in a new window]

Abstract.

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The main result of this paper establishes the existence and uniqueness of integral representations of KMS functionals on nuclear *- algebras. Our first result is about representations of *-algebras by means of operators having a common dense domain in a Hilbert space. We show, under certain regularity conditions, that (Powers) self-adjoint representations of a nuclear *-algebra, which admit a direct integral decomposition, disintegrate into representations which are almost all self-adjoint. We then define and study the class of self-derivative algebras. All algebras with an identity are in this class and many other examples are given. We show that if 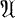is a self-derivative algebra with an equicontinuous approximate identity, the cone of all positive forms on 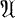is isomorphic to the cone of all positive invariant kernels on 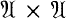These in turn correspond bijectively to the invariant Hilbert subspaces of the dual space 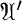This shows that if 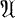is a nuclear 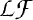-space, the positive cone of 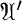has bounded order intervals, which implies that each positive form on 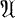has an integral representation in terms of the extreme generators of the cone. Given a continuous exponentially bounded one-parameter group of *-automorphisms of 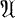we can define the subcone of all invariant positive forms satisfying the KMS condition. Central functionals can be viewed as KMS functionals with respect to a trivial group action. Assuming that 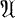is a self-derivative algebra with an equicontinuous approximate identity, we show that the face generated by a self-adjoint KMS functional is a lattice. If 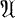is moreover a nuclear 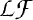*-algebra the previous results together imply that each self-adjoint KMS functional has a unique integral representation by means of extreme KMS functionals almost all of which are self-adjoint.

Keywords

46 K 1046 A 1252 A 0746 H 0581 E 0582 A 15Nuclear spacereproducing kernels of Hilbert subspacestopological *-algebraself-adjoint representationcentral and KMS statesintegral representation
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 42 , Issue 3 , 01 June 1990 , pp. 410 - 469
Copyright
Copyright © Canadian Mathematical Society 1990

References

1. Araki, H., Introduction to Operator Algebras, in Stat. Mech. & Field theory, Sen, R.N. and Weil, C. editors, Halsted Press, New York 1972.Google Scholar
2. Bonsall, F. and Duncan, J., Complete Normed Algebras, Springer-Verlag, New York-Heidelberg- Berlin 1973.Google Scholar
3. Borchers, H.J., Algebraic aspects of Wightman field theory, in Stat. Mechanics & Field theory, edited by Sein, R.N. and Weil, C., Halsted Press, New York 1972.Google Scholar
4. Borchers, H.J. and Yngvason, J., On the Algebra of Field operators. The Weak commutant andIntegral Decompositions of states, Comm. Math. Phys. 42 (1975) 231–252.Google Scholar
5. Bourbaki, N., N, Topologie générale chap. 1 à 4, Hermann, Paris 1971.Google Scholar
6. Bourbaki, N., Intégration livre IV, Hermann, Paris 1963.Google Scholar
7. Bratteli, O. and Robinson, D.W., Operator Algebras and Quantum Statistical Mechanics, vol. I and II, Springer-Verlag, New York-Heidelberg-Berlin 1979 and 1981.Google Scholar
8. Dixmier, J. and Malliavin, P., Factorisations de fonctions et de vecteurs indéfiniment diffèrentiables,, Bull. Soc. Math. France 2e série 102 (1978) 321–344.Google Scholar
9. Dunford, N. and Schwartz, J., Linear Operators, Part I, Wiley, New York, 1966.Google Scholar
10. Eymard, P., L'algèbre de Fourier d un groupe localement compact, Bull. Soc. Math. France 92 (1964) 181–236.Google Scholar
11. Fulling, S.A. and Ruijsenaars, S.N. M., Temperature, Periodicity and Horizons, Physics Reports 152 no. 3 (1987) 135–176.Google Scholar
12. Grothendieck, A., Espaces vectoriels topologiques, Sao Paulo 1954.Google Scholar
13. Grothendieck, A., Produits tensoriels topologiques et espaces nucléaires, Memoirs of AMS 16, 1955.Google Scholar
14. Haag, R., Hugenholtz, N.M. and Winnink, M., On the equilibrium states in quantum statisticalmechanics, Comm. in Math. Phys. 5 (1967) 215- 236.Google Scholar
15. Hegerfeldt, G.C., Extremal decomposition of Whightman functions and of states on nuclear*-algebras by Choquet theory, Comm. in Math. Phys. 45 (1975) 133–135.Google Scholar
16. Kubo, R., Statistical-Mechanical Theory of irreversible Processes, I. General Theory and simple Applications to magnetic and Conduction Problems, J. Phys. Soc. Japan, 12 (1967) 570–586.Google Scholar
17. Lanford, O.E. and Ruelle, D., Integral representations of invariant states on B*-algebras, J. Math. Phys. 8 (1967) 1460–1463.Google Scholar
18. Maurin, K., General eigenfunction expansions and unitary representations of topological groups, Polish Scientific Publishers, Warsaw 1968.Google Scholar
19. Martin, P.C. and Schwinger, J., Theory of Many Particles Systems, I, Phys. Rev. 115 (1959) 1342–1373.Google Scholar
20. Naimark, N.A., Normed Rings, Wolters-Noordhoff, Groningen 1970.Google Scholar
21. Pietsch, A. , Nuclear locally convex spaces, Springer-Verlag, New York-Heidelberg-Berlin 1972.Google Scholar
22. Powers, R.T., Self-adjoint algebras of unbounded operators, Comm. in Math. Phys. 21 (1971) 85–124.Google Scholar
23. Powers, R.T., Self-adjoint algebras of unbounded operators, II, Trans, of AMS 187 (1974) 261–293.Google Scholar
24. Ruelle, D., Symmetry breakdown in statistical mechanics, Cargèse lectures in Physics, Vol. 4, ed. by Kastler, D., Gordon and Breach, New-York 1970.Google Scholar
25. Schwartz, L., Sous-espaces hilbertiens d'espaces vectoriels topologiques et noyaux associés,, Journal d'Anal. Math. 13 (1964) 115–256.Google Scholar
26. Schwartz, L., Radon measures on arbitrary topological spaces and cylindrical measures, Oxford University Press 1973.Google Scholar
27. Shermann, S., Order in operator algebras, Amer. Jour, of Math. vol. 73 (1951), 227–232.Google Scholar
28. Thomas, E.G.F., Integral representations in conuclear cones, Preprint, University of Groningen 1988.Google Scholar
29. Thomas, E.G.F., Analysis in embedded Hubert spaces, Lecture Notes, Preprint University of Groningen 1988.Google Scholar
30. Thomas, E.G.F., The theorem of Bochner-Schwartz-Godement for generalized Gelfand pairs, Proc. 3rd Paderborn conference in Functional Analysis, North-Holland Publ. Co. 1983.Google Scholar