Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Noussair, Ezzat S.
Swanson, Charles A.
and
Jianfu, Yang
1993.
Quasilinear elliptic problems with critical exponents.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 20,
Issue. 3,
p.
285.
Swanson, C.A.
1995.
Uniqueness for semilinear polyharmonic problems.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 25,
Issue. 9-10,
p.
1055.
Santanilla, Jairo
1995.
Existence and nonexistence of positive radial solutions of an elliptic Dirichlet problem in an exterior domain.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 25,
Issue. 12,
p.
1391.
Noussair, E.S.
and
Jianfu, Yang
1996.
On the existence of multiple positive solutions of critical semilinear elliptic problems.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 26,
Issue. 8,
p.
1323.
Noussair, Ezzat S.
and
Swanson, Charles A.
1996.
Multiple finite energy states for critical potential systems.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 26,
Issue. 2,
p.
217.
Miyagaki, Olimpio Hiroshi
1997.
On a class of semilinear elliptic problems in ℝN with critical growth.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 29,
Issue. 7,
p.
773.
Alves, C.O.
Goncalves, J.V.
and
Miyagaki, O.H.
1998.
Multiple positive solutions for semilinear elliptic equations in ℝ involving critical exponents.
Nonlinear Analysis,
Vol. 34,
Issue. 4,
p.
593.
Gonçalves, J.V.
and
Alves, C.O.
1998.
Existence of positive solutions for m-Laplacian equations in N involving critical Sobolev exponents.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 32,
Issue. 1,
p.
53.
Noussair, E.S.
and
Yan, Shusen
2001.
The scalar curvature equation on.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 45,
Issue. 4,
p.
483.
Kang, Dongsheng
and
Deng, Yinbin
2003.
Existence of solution for a singular critical elliptic equation.
Journal of Mathematical Analysis and Applications,
Vol. 284,
Issue. 2,
p.
724.
Deng, Yinbin
Ma, Yaming
and
Zhao, Charles Xuejin
2005.
Existence and Properties of Multiple Positive Solutions for Semi-Linear Equations with Critical Exponents.
Rocky Mountain Journal of Mathematics,
Vol. 35,
Issue. 5,
Orpel, Aleksandra
2019.
Uncountable sets of finite energy solutions for semilinear elliptic problems in exterior domains.
Journal of Mathematical Analysis and Applications,
Vol. 472,
Issue. 1,
p.
1175.
CARRIÃO, PAULO CESAR
COSTA, AUGUSTO CÉSAR DOS REIS
and
MIYAGAKI, OLIMPIO HIROSHI
2020.
A CLASS OF CRITICAL KIRCHHOFF PROBLEM ON THE HYPERBOLIC SPACE.
Glasgow Mathematical Journal,
Vol. 62,
Issue. 1,
p.
109.


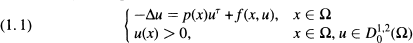
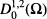 is the completion of
is the completion of 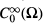 in the L2(Ω) norm of
in the L2(Ω) norm of 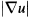 .
.