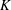Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-26T07:20:52.878Z Has data issue: false hasContentIssue false
  • English
  • Français

Polynomials from Combinatorial $K$-theory

Part of: Algebraic combinatorics

Published online by Cambridge University Press:  03 September 2019

Cara Monical ,
Oliver Pechenik  and
Dominic Searles
Cara Monical
Affiliation:
Department of Mathematics, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA Email: [email protected]
Oliver Pechenik
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, MI 48109, USA Email: [email protected]
Dominic Searles
Affiliation:
Department of Mathematics and Statistics, University of Otago, Dunedin9016, New Zealand Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce two new bases of the ring of polynomials and study their relations to known bases. The first basis is the quasi-Lascoux basis, which is simultaneously both a 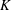$K$-theoretic deformation of the quasi-key basis and also a lift of the 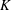$K$-analogue of the quasi-Schur basis from quasi-symmetric polynomials to general polynomials. We give positive expansions of this quasi-Lascoux basis into the glide and Lascoux atom bases, as well as a positive expansion of the Lascoux basis into the quasi-Lascoux basis. As a special case, these expansions give the first proof that the 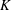$K$-analogues of quasi-Schur polynomials expand positively in multifundamental quasi-symmetric polynomials of T. Lam and P. Pylyavskyy.

The second new basis is the kaon basis, a 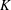$K$-theoretic deformation of the fundamental particle basis. We give positive expansions of the glide and Lascoux atom bases into this kaon basis.

Throughout, we explore how the relationships among these 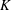$K$-analogues mirror the relationships among their cohomological counterparts. We make several “alternating sum” conjectures that are suggestive of Euler characteristic calculations.

Keywords

Demazure characterDemazure atomLascoux polynomialLascoux atomGrothendieck polynomialquasi-Lascoux polynomialkaon

MSC classification

Primary: 05E05: Symmetric functions and generalizations
Type
Article
Information
Canadian Journal of Mathematics , Volume 73 , Issue 1 , February 2021 , pp. 29 - 62
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Author C.M. was partially supported by a GAANN Fellowship from the Department of Mathematics, University of Illinois at Urbana-Champaign. Author O.P. was partially supported by a Mathematical Sciences Postdoctoral Research Fellowship (#1703696) from the National Science Foundation.

References

Assaf, S., Nonsymmetric Macdonald polynomials and a refinement of Kostka–Foulkes polynomials. Trans. Amer. Math. Soc. 370(2018), no. 12, 8777–8796. https://doi.org/10.1090/tran/7374CrossRefGoogle Scholar
Assaf, S. and Searles, D., Schubert polynomials, slide polynomials, Stanley symmetric functions and quasi-Yamanouchi pipe dreams. Adv. Math. 306(2017), 89–122. https://doi.org/10.1016/j.aim.2016.10.015CrossRefGoogle Scholar
Assaf, S. and Schilling, A., A Demazure crystal construction for Schubert polynomials. Algebr. Comb. 1(2018), no. 2, 225–247.Google Scholar
Assaf, S. and Searles, D., Kohnert tableaux and a lifting of quasi-Schur functions. J. Combin. Theory Ser. A 156(2018), 85–118. https://doi.org/10.1016/j.jcta.2018.01.001CrossRefGoogle Scholar
Bressler, P. and Evens, S., The Schubert calculus, braid relations, and generalized cohomology. Trans. Amer. Math. Soc. 317(1990), no. 2, 799–811. https://doi.org/10.2307/2001488CrossRefGoogle Scholar
Buch, A. S., A Littlewood-Richardson rule for the K-theory of Grassmannians. Acta Math. 189(2002), no. 1, 37–78. https://doi.org/10.1007/BF02392644CrossRefGoogle Scholar
Calmès, B., Zainoulline, K., and Zhong, C., Equivariant oriented cohomology of flag varieties. Doc. Math. 2015(2015), no. Extra vol.: Alexander S. Merkurjev’s sixtieth birthday, 113–144.Google Scholar
Demazure, M., Une nouvelle formule des caractères. Bull. Sci. Math. (2) 98(1974), no. 3, 163–172.Google Scholar
Fomin, S. and Kirillov, A. N., Grothendieck polynomials and the Yang–Baxter equation. In: Formal power series and algebraic combinatorics/Séries formelles et combinatoire algébrique. DIMACS, Piscataway, NJ, 1994, pp. 183–189.Google Scholar
Gessel, I. M., Multipartite P-partitions and inner products of skew Schur functions. In: Combinatorics and algebra (Boulder, Colo., 1983). Contemp. Math., 34, Amer. Math. Soc., Providence, RI, 1984, pp. 289–317. https://doi.org/10.1090/conm/034/777705CrossRefGoogle Scholar
Ganter, N. and Ram, A., Generalized Schubert calculus. J. Ramanujan Math. Soc. 28A(2013), 149–190.Google Scholar
Haglund, J., Luoto, K., Mason, S., and van Willigenburg, S., Quasisymmetric Schur functions. J. Combin. Theory Ser. A 118(2011), no. 2, 463–490.CrossRefGoogle Scholar
Haglund, J., Luoto, K., Mason, S., and van Willigenburg, S., Refinements of the Littlewood–Richardson rule. Trans. Amer. Math. Soc. 363(2011), no. 3, 1665–1686. https://doi.org/10.1090/S0002-9947-2010-05244-4CrossRefGoogle Scholar
Hudson, T., A Thom–Porteous formula for connective K-theory using algebraic cobordism. J. K-Theory 14(2014), no. 2, 343–369. https://doi.org/10.1017/is014005031jkt266CrossRefGoogle Scholar
Kirillov, A. N., Notes on Schubert, Grothendieck and key polynomials. SIGMA Symmetry Integrability Geom. Methods Appl. 12(2016), Paper No. 034, 1–56. https://doi.org/10.3842/SIGMA.2016.034Google Scholar
Knutson, A., Tao, T., and Woodward, C., The honeycomb model of GLn(ℂ) tensor products. II. Puzzles determine facets of the Littlewood–Richardson cone. J. Amer. Math. Soc. 17(2004), no. 1, 19–48. https://doi.org/10.1090/S0894-0347-03-00441-7CrossRefGoogle Scholar
Kohnert, A., Weintrauben, Polynome, Tableaux. Dissertation, Universität Bayreuth, Bayreuth, 1990. Bayreuth. Math. Schr. 38(1991), 1–97.Google Scholar
Lam, T. and Pylyavskyy, P., Combinatorial Hopf algebras and K-homology of Grassmannians. Int. Math. Res. Not. IMRN 2007(2007), no. 24, 1–48. https://doi.org/10.1093/imrn/rnm125Google Scholar
Lascoux, A., Transition on Grothendieck polynomials. In: Physics and combinatorics, 2000 (Nagoya). World Sci. Publ., River Edge, NJ, 2001, pp. 164–179.Google Scholar
Lascoux, A., Polynomials. 2013. http://www-igm.univ-mlv.fr/∼al/ARTICLES/CoursYGKM.pdfGoogle Scholar
Lascoux, A. and Schützenberger, M.-P., Structure de Hopf de l’anneau de cohomologie et de l’anneau de Grothendieck d’une variété de drapeaux. C. R. Acad. Sci. Paris Sér. I Math. 295(1982), no. 11, 629–633.Google Scholar
Lascoux, A. and Schützenberger, M.-P., Keys and standard bases. In: Invariant theory and tableaux (Minneapolis, MN, 1988). IMA Vol. Math. Appl., 19, Springer, New York, 1990, pp. 125–144.Google Scholar
Lenart, C. and Zainoulline, K., A Schubert basis in equivariant elliptic cohomology. New York J. Math. 23(2017), 711–737.Google Scholar
Littlewood, D. E. and Richardson, A. R., Group characters and algebra. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 233(1934), 99–141.Google Scholar
Mason, S., A decomposition of Schur functions and an analogue of the Robinson–Schensted–Knuth algorithm. Sém. Lothar. Combin. 57(2006/08), B57e.Google Scholar
Mason, S., An explicit construction of type A Demazure atoms. J. Algebraic Combin. 29(2009), no. 3, 295–313. https://doi.org/10.1007/s10801-008-0133-4CrossRefGoogle Scholar
Monical, C., Set-valued skyline fillings. Sém. Lothar. Combin. 78B(2017), Art. 35.Google Scholar
Monical, C., Pechenik, O., and Scrimshaw, T., Crystal structures for symmetric Grothendieck polynomials. (2018). arxiv:1807.03294Google Scholar
Pechenik, O. and Searles, D., Decompositions of Grothendieck polynomials. Int. Math. Res. Not. 2019, no. 10, 3214–3241. https://doi.org/10.1093/imrn/rnx207CrossRefGoogle Scholar
Pechenik, O. and Yong, A., Genomic tableaux. J. Algebraic Combin. 45(2017), no. 3, 649–685. https://doi.org/10.1007/s10801-016-0720-8CrossRefGoogle Scholar
Pun, A. Y., On deposition of the product of Demazure atoms and Demazure characters. Ph.D. thesis, University of Pennsylvania, 2016. arxiv:1606.02291Google Scholar
Reiner, V. and Shimozono, M., Key polynomials and a flagged Littlewood–Richardson rule. J. Combin. Theory Ser. A 70(1995), no. 1, 107–143. https://doi.org/10.1016/0097-3165(95)90083-7CrossRefGoogle Scholar
Ross, C. and Yong, A., Combinatorial rules for three bases of polynomials. Sém. Lothar. Combin. 74(2015–2018), Art. B74a.Google Scholar
Searles, D., Polynomial bases: positivity and Schur multiplication. Trans. Amer. Math. Soc. 373(2020), 819–847. https://doi.org/10.1090/tran/7670CrossRefGoogle Scholar
Thomas, H. and Yong, A., A jeu de taquin theory for increasing tableaux, with applications to K-theoretic Schubert calculus. Algebra Number Theory 3(2009), no. 2, 121–148. https://doi.org/10.2140/ant.2009.3.121CrossRefGoogle Scholar
Vakil, R., A geometric Littlewood–Richardson rule. Appendix A written with A. Knutson. Ann. of Math. (2) 164(2006), no. 2, 371–421. https://doi.org/10.4007/annals.2006.164.371Google Scholar