Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-11T02:20:43.575Z Has data issue: false hasContentIssue false
  • English
  • Français

Polynomiality of factorizations in reflection groups

Part of: Special aspects of infinite or finite groups Combinatorics

Published online by Cambridge University Press:  09 December 2021

Elzbieta Polak  and
Dustin Ross
Elzbieta Polak
Affiliation:
Department of Mathematics, University of Texas at Austin, Austin, TX, USA e-mail: [email protected]
Dustin Ross*
Affiliation:
Department of Mathematics, San Francisco State University, San Francisco, CA, USA
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the number of ways of factoring elements in the complex reflection groups 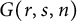$G(r,s,n)$ as products of reflections. We prove a result that compares factorization numbers in 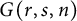$G(r,s,n)$ to those in the symmetric group 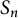$S_n$ , and we use this comparison, along with the Ekedahl, Lando, Shapiro, and Vainshtein (ELSV) formula, to deduce a polynomial structure for factorizations in 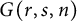$G(r,s,n)$ .

Keywords

Reflection groupsfactorizationsELSV formulapolynomiality

MSC classification

Primary: 20F55: Reflection and Coxeter groups
Secondary: 05A15: Exact enumeration problems, generating functions
Type
Article
Information
Canadian Journal of Mathematics , Volume 75 , Issue 1 , February 2023 , pp. 245 - 266
Check for updates
Copyright
© Canadian Mathematical Society, 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bini, G., Goulden, I. P., and Jackson, D. M., Transitive factorizations in the hyperoctahedral group. Canad. J. Math. 60(2008), no. 2, 297–312.CrossRefGoogle Scholar
Cavalieri, R. and Miles, E., Riemann surfaces and algebraic curves, London Mathematical Society Student Texts, 87, Cambridge University Press,Cambridge, 2016.CrossRefGoogle Scholar
Chapuy, G. and Stump, C., Counting factorizations of Coxeter elements into products of reflections. J. Lond. Math. Soc. (2) 90(2014), no. 3, 919–939.CrossRefGoogle Scholar
delMas, E., Hameister, T., and Reiner, V., A refined count of Coxeter element reflection factorizations. Electron. J. Combin. 25(2018), no. 1, Paper 1.28, 11.CrossRefGoogle Scholar
Douvropoulos, T., On enumerating factorizations in reflection groups. Sém. Lothar. Combin. 82(B)(2020), 12.Google Scholar
Ekedahl, T., Lando, S., Shapiro, M., and Vainshtein, A., Hurwitz numbers and intersections on moduli spaces of curves. Invent. Math. 146(2001), no. 2, 297–327.CrossRefGoogle Scholar
Goulden, I. P., Jackson, D. M., and Vainshtein, A., The number of ramified coverings of the sphere by the torus and surfaces of higher genera. Ann. Comb. 4(2000), no. 1, 27–46.CrossRefGoogle Scholar
Hurwitz, A., Ueber Riemann’sche Flächen mit gegebenen Verzweigungspunkten. Math. Ann. 39(1891), no. 1, 1–60.Google Scholar
Jackson, D. M., Some combinatorial problems associated with products of conjugacy classes of the symmetric group. J. Combin. Theory Ser. A 49(1988), no. 2, 363–369.CrossRefGoogle Scholar
Lewis, J. B. and Morales, A. H., Factorization problems in complex reflection groups. Canad. J. Math. 73(2021), no. 4, 899–946.CrossRefGoogle Scholar
Michel, J., Deligne-Lusztig theoretic derivation for Weyl groups of the number of reflection factorizations of a Coxeter element. Proc. Amer. Math. Soc. 144(2016), no. 3, 937–941.CrossRefGoogle Scholar
Shephard, G. C. and Todd, J. A., Finite unitary reflection groups. Canad. J. Math. 6(1954), 274–304.CrossRefGoogle Scholar