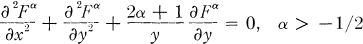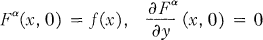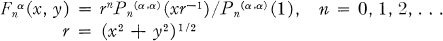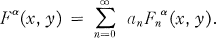Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
McCoy, Peter A.
1979.
Mean boundary value problems for a class of elliptic equations in 𝐸³.
Proceedings of the American Mathematical Society,
Vol. 76,
Issue. 1,
p.
123.
McCoy, Peter A
1980.
A mean boundary value problem for a generalized axisymmetric potential on doubly connected regions.
Journal of Mathematical Analysis and Applications,
Vol. 76,
Issue. 1,
p.
213.
McCoy, Peter A.
1980.
Best 𝐿^{𝑝}-approximation of generalized biaxisymmetric potentials.
Proceedings of the American Mathematical Society,
Vol. 79,
Issue. 3,
p.
435.
McCoy, Peter A.
1992.
Solutions of the helmholtz equation having rapid growth.
Complex Variables, Theory and Application: An International Journal,
Vol. 18,
Issue. 1-2,
p.
91.
Srivastava, G. S.
1996.
Approximation and growth of generalized axisymmetric potentials.
Approximation Theory and its Applications,
Vol. 12,
Issue. 4,
p.
96.
Hasanov, Anvar
2007.
Fundamental solutions of generalized bi-axially symmetric Helmholtz equation.
Complex Variables and Elliptic Equations,
Vol. 52,
Issue. 8,
p.
673.
Salakhitdinov, M. S.
and
Hasanov, A.
2008.
A solution of the Neumann–Dirichlet boundary value problem for generalized bi-axially symmetric Helmholtz equation.
Complex Variables and Elliptic Equations,
Vol. 53,
Issue. 4,
p.
355.
Hasanov, Anvar
and
Karimov, E.T.
2009.
Fundamental solutions for a class of three-dimensional elliptic equations with singular coefficients.
Applied Mathematics Letters,
Vol. 22,
Issue. 12,
p.
1828.
Karimov, E.T.
2010.
On a boundary problem with Neumann’s condition for 3D singular elliptic equations.
Applied Mathematics Letters,
Vol. 23,
Issue. 5,
p.
517.
Nieto, J. J.
and
Karimov, E. T.
2012.
ON AN ANALOGUE OF THE HOLMGREN'S PROBLEM FOR 3D SINGULAR ELLIPTIC EQUATION.
Asian-European Journal of Mathematics,
Vol. 05,
Issue. 02,
p.
1250021.
H. Khan, Huzoor
and
Ali, Rifaqat
2012.
Slow Growth and Approximation of Entire Solution of Generalized Axially Symmetric Helmholtz Equation.
Asian Journal of Mathematics & Statistics,
Vol. 5,
Issue. 4,
p.
104.
Kim, Yong-Sup
and
Hasanov, Anvar
2012.
FUNCTIONAL RELATIONS INVOLVING SARAN'S HYPERGEOMETRIC FUNCTIONS FEAND F(3).
The Pure and Applied Mathematics,
Vol. 19,
Issue. 1,
p.
43.
Choi, June-Sang
Hasanov, Anvar
and
Turaev, Mamasali
2012.
Serendipitous Functional Relations Deducible from Certain Generalized Triple Hypergeometric Functions.
Kyungpook mathematical journal,
Vol. 52,
Issue. 2,
p.
109.
Bin-Saad, Maged G.
and
Hasanov, Anvar
2014.
Linear Independent Solutions and Operational Representations for Hypergeometric Functions of Four Variables.
Chinese Journal of Mathematics,
Vol. 2014,
Issue. ,
p.
1.
Mavlyaviev, R. M.
and
Garipov, I. B.
2017.
Fundamental solution of multidimensional axisymmetric Helmholtz equation.
Complex Variables and Elliptic Equations,
Vol. 62,
Issue. 3,
p.
287.
Ergashev, Tuhtasin G.
2018.
The Dirichlet problem for elliptic equation with several singular coefficients.
e-Journal of Analysis and Applied Mathematics,
Vol. 2018,
Issue. 1,
p.
81.
Muydinjanov, Davlatjon R.
2019.
Holmgren problem for Helmholtz equation with the three singular coefficients.
e-Journal of Analysis and Applied Mathematics,
Vol. 2019,
Issue. 1,
p.
15.
Berdyshev, A. S.
Hasanov, A.
and
Ergashev, T.
2020.
Double-layer potentials for a generalized bi-axially symmetric Helmholtz equation II.
Complex Variables and Elliptic Equations,
Vol. 65,
Issue. 2,
p.
316.
Hasanov, A.
Berdyshev, A. S.
and
Ryskan, A. R.
2020.
Fundamental solutions for a class of four-dimensional degenerate elliptic equation.
Complex Variables and Elliptic Equations,
Vol. 65,
Issue. 4,
p.
632.
Bin-Saad, Maged G.
Hasanov, Anvar
and
Younis, Jihad A.
2021.
Fundamental solutions of the generalized axially symmetric Helmholtz equation
.
Novi Sad Journal of Mathematics,
Vol. 52,
Issue. 2,
p.
127.