Article contents
Poles of the Standard 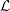 ${\mathcal{L}}$-function of
${\mathcal{L}}$-function of 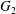 $G_{2}$ and the Rallis–Schiffmann Lift
$G_{2}$ and the Rallis–Schiffmann Lift
Published online by Cambridge University Press: 07 March 2019
Abstract
We characterize the cuspidal representations of 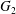 $G_{2}$ whose standard
$G_{2}$ whose standard 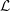 ${\mathcal{L}}$-function admits a pole at
${\mathcal{L}}$-function admits a pole at 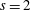 $s=2$ as the image of the Rallis–Schiffmann lift for the commuting pair (
$s=2$ as the image of the Rallis–Schiffmann lift for the commuting pair (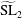 $\widetilde{\text{SL}}_{2}$,
$\widetilde{\text{SL}}_{2}$, 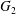 $G_{2}$) in
$G_{2}$) in 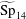 $\widetilde{\text{Sp}}_{14}$. The image consists of non-tempered representations. The main tool is the recent construction, by the second author, of a family of Rankin–Selberg integrals representing the standard
$\widetilde{\text{Sp}}_{14}$. The image consists of non-tempered representations. The main tool is the recent construction, by the second author, of a family of Rankin–Selberg integrals representing the standard 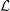 ${\mathcal{L}}$-function.
${\mathcal{L}}$-function.
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2019
Footnotes
The authors were partially supported by grants 1691/10 and 259/14 from the Israel Science Foundation.
References
- 1
- Cited by


