Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T01:06:13.662Z Has data issue: false hasContentIssue false
  • English
  • Français

The Poincaré Series Of Stretched Cohen-Macaulay Rings

Published online by Cambridge University Press:  20 November 2018

Judith D. Sally
Judith D. Sally*
Affiliation:
Northwestern University, Evanston, Illinois
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

There are relatively few classes of local rings (R, m) for which the question of the rationality of the Poincaré series

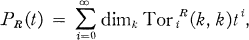
where k = R/m, has been settled. (For an example of a local ring with non-rational Poincaré series see the recent paper by D. Anick, “Construction of loop spaces and local rings whose Poincaré—Betti series are nonrational”, C. R. Acad. Sc. Paris 290 (1980), 729-732.) In this note, we compute the Poincaré series of a certain family of local Cohen-Macaulay rings and obtain, as a corollary, the rationality of the Poincaré series of d-dimensional local Gorenstein rings (R, m) of embedding dimension at least e + d – 3, where e is the multiplicity of R. It follows that local Gorenstein rings of multiplicity at most five have rational Poincaré series.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 5 , 01 October 1980 , pp. 1261 - 1265
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Abhyankar, S. S., Local rings of high embedding dimension, Amer. J. Math. 89 (1967), 1073–1077.Google Scholar
2. Gulliksen, T. H. and Levin, G., Homology of local rings, Queen's Papers in Pure and Applied Math 20 (Queen's University, Kingston, Ontario, 1969).Google Scholar
3. Levin, G., Lectures on Golod homomorphisms, preprint No. 15 (1976), Matematiska institutionem Stockholms universitet.Google Scholar
4. Northcott, D. G. and Rees, D., Reductions of ideals in local rings, Proc. Camb. Phil. Soc. 50 (1954), 145–158.Google Scholar
5. Rahbar-Rochandel, H., Relation entre la série de Betti d'un anneau local de Gorenstein R et celle de anneau R/socle (R), C. R. Acad. Se. Paris 284 (1977), 651–654.Google Scholar
6. Sally, J. D., Cohen-Macaulay local rings of maximal embedding dimension, J. of Alg. 56 (1979), 168–183.Google Scholar
7. Sally, J. D., Stretched Gorenstein rings, J. London Math. Soc. 20 (1979), 19–26.Google Scholar
8. Tate, J., Homology of Noetherian rings and local rings, 111. J. of Math. 1 (1957), 14–25.Google Scholar