Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hoffman, P.
1983.
Exponential maps and λ-rings.
Journal of Pure and Applied Algebra,
Vol. 27,
Issue. 2,
p.
131.


 , where
, where 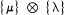 is the ‘new multiplication' or plethysm of D. E. Littlewood [
is the ‘new multiplication' or plethysm of D. E. Littlewood [ . The aim of this paper is to define the latter representation and deduce its character using a somewhat different approach from that in [
. The aim of this paper is to define the latter representation and deduce its character using a somewhat different approach from that in [