Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T02:13:56.017Z Has data issue: false hasContentIssue false
  • English
  • Français

Planar Sublattices of a Free Lattice. II

Published online by Cambridge University Press:  20 November 2018

Ivan Rival  and
Bill Sands
Ivan Rival
Affiliation:
University of Calgary, Calgary, Alberta
Bill Sands
Affiliation:
University of Manitoba, Winnipeg, Manitoba
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In Planar sublattices of a free lattice, I [8] we verify Jonsson's conjecture for finite planar lattices; in particular we obtain a characterization of finite planar sublattices of a free lattice among all finite lattices. In the present paper we use arguments of a quite different flavour to obtain another characterization. Let

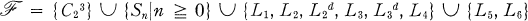
be the family of lattices illustrated in Figures 1, 2, 3, and 4. Our goal is to prove the following theorem: a finite lattice is a planar sublattice of a free lattice if andonly if it does not have a member of 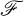as a sublattice.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 1 , 01 February 1979 , pp. 17 - 34
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Antonius, R. and Rival, I., A note on Whitman s property for free lattices, Alg. Univ. 4 (1974), 271–272.Google Scholar
2. Davey, B. A., Poguntke, W., and Rival, I., A characterization of semidistributivity, Alg. Univ. 5 (1975), 72–75.Google Scholar
3. Jônsson, B., Sublattices of a free lattice, Can. J. Math. 13 (1961), 256–264.Google Scholar
4. Jônsson, B. and Kiefer, J., Finite sublattices of a free lattice, Can. J. Math. 14 (1962), 487–497.Google Scholar
5. Kelly, D. and Rival, I., Crowns, fences, and dismantlable lattices, Can. J. Math. 26 (1974), 1257–1271.Google Scholar
6. Kelly, D. and Rival, I., Planar lattices, Can. J. Math. 27 (1975), 636–665.Google Scholar
7. Kelly, D. and Rival, I., Certain partially ordered sets of dimension three, J. Combinatorial Theor. 18 (1975), 239–242.Google Scholar
8. Rival, I. and Sands, B., Planar sublattices of a free lattice I, Can. J. Math. (1978).Google Scholar
9. Whitman, P. M., Free lattices, Ann. of Math. 42 (1941), 325–330.Google Scholar