Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T00:58:27.412Z Has data issue: false hasContentIssue false
  • English
  • Français

Petits points d’une surface

Published online by Cambridge University Press:  20 November 2018

Corentin Pontreau
Corentin Pontreau*
Affiliation:
Laboratoire de mathématiques Nicolas Oresme, Université de Caen BP 5186, 14032 Caen Cedex, France, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Résumé

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Pour toute sous-vari ét é géométriquement irréductible 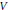$V$ du groupe multiplicatif 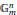$\mathbb{G}_{m}^{n}$, on sait qu’en dehors d’un nombre fini de translat és de tores exceptionnels inclus dans 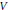$V$, tous les points sont de hauteur minorée par une certaine quantité 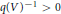$q{{(V)}^{-1}}>0$. On connaît de plus une borne supérieure pour la somme des degrés de ces translatés de tores pour des valeurs de 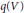$q(V)$ polynomiales en le degré de 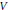$V$. Ceci n’est pas le cas si l’on exige une minoration quasi-optimale pour la hauteur des points de 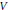$V$, essentiellement linéaire en l’inverse du degré.

Nous apportons ici une réponse partielle à ce problème : nous donnons une majoration de la somme des degrés de ces translat és de sous-tores de codimension 1 d’une hypersurface 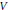$V$. Les résultats, obtenus dans le cas de 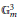$\mathbb{G}_{m}^{3}$,mais complètement explicites, peuvent toutefois s’étendre à 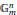$\mathbb{G}_{m}^{n}$,moyennant quelques petites complications inhérentes à la dimension $n$.

Keywords

11G5011J8111G40Hauteur normaliséegroupe multiplicatifproblème de Lehmerpetits points
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 5 , 01 October 2009 , pp. 1118 - 1150
Copyright
Copyright © Canadian Mathematical Society 2009

References

Références

[1] Amoroso, F. and David, S., Le problème de Lehmer en dimension supérieure. J. Reine Angew. Math. 513(1999), 145–179.Google Scholar
[2] Amoroso, F. and David, S., Densité des points à coordonnées multiplicativement indépendantes. Ramanujan J. 5(2001), no. 3, 237–246.Google Scholar
[3] Amoroso, F. and David, S., Minoration de la hauteur normalisée dans un tore. J. Inst. Math. Jussieu 2(2003), no. 3, 335–381.Google Scholar
[4] Amoroso, F. and David, S., Distribution des points de petite hauteur dans les groupes multiplicatifs. Ann. Sc. Norm. Super. Pisa Cl. Sci. 3(2004), no. 2, 325–348.Google Scholar
[5] Amoroso, F. and David, S., Points de petite hauteur sur une sous-variété d’un tore. Compos. Math. 142(2006), no. 3, 551–562.Google Scholar
[6] Bombieri, E. and Zannier, U., Algebraic points on subvarieties of Gn m. Internat. Math. Res. Notices 1995, no. 7, 333–347.Google Scholar
[7] David, S. and Philippon, P., Minorations des hauteurs normalisées des sous-variétés de variétés abéliennes. In: Number Theory. Contemp. Math. 210, American Mathematical Society, Providence, RI, 1998, pp. 333–364.Google Scholar
[8] David, S. and Philippon, P., Minorations des hauteurs normalisées des sous-variétés des tores. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 28(1999), no. 3, 489–543.Google Scholar
[9] David, S. and Philippon, P., Errata à: Minorations des hauteurs normalisées des sous-variétés des tores. Ann. Scuola Norm. Sup. Sci. Pisa Cl. Sci. 29(2000), no. 3, 729–731.Google Scholar
[10] Hindry, M., Autour d’une conjecture de Serge Lang. Invent. Math. 94(1988), no. 3, 575–603.Google Scholar
[11] Philippon, P., Lemmes de zéros dans les groupes algébriques commutatifs. Bull. Soc. Math. France 114(1986), no. 3, 355–383.Google Scholar
[12] Pontreau, C., Minoration effective de la hauteur des points d’une courbe de G2 m définie sur Q. Acta Arith. 120(2005), no. 1, 1–26.Google Scholar
[13] Pontreau, C., Geometric lower bounds for the normalized height of hypersurfaces. Int. J. Number Theory 2(2006), no. 4, 555–568.Google Scholar
[14] Rosser, J. B. and Schoenfeld, L., Approximate formulas for some functions of prime numbers. Illinois J. Math. 6(1962), 64–94.Google Scholar
[15] Schmidt, W. M., Heights of points on subvarieties of Gn m. In: Number Theory. London Math. Soc. Lecture Note Ser. 235, Cambridge University Press, 1996, pp. 157–187.Google Scholar
[16] Zhang, S., Positive line bundles on arithmetic varieties. J. Amer. Math. Soc. 8(1995), no. 1, 187–221.Google Scholar
[17] Zhang, S., Small points and adelic metrics. J. Algebraic Geom. 4(1995), no. 2, 281–300.Google Scholar