Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-20T17:37:52.025Z Has data issue: false hasContentIssue false
  • English
  • Français

A Permanental Inequality—The Case of Equality

Published online by Cambridge University Press:  20 November 2018

Marvin Marcus  and
Henryk Minc
Marvin Marcus
Affiliation:
University of California, Santa Barbara
Henryk Minc
Affiliation:
University of California, Santa Barbara
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In (3) we proved that if A is a complex n-square normal matrix with characteristic roots α1 … , αn,then

1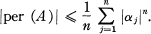

If A is positive semi-definite hermitian, the inequality (1) becomes

2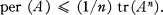

This inequality partially answers the problem of determining the maximum permanent of a positive semi-definite hermitian matrix with prescribed characteristic roots (6). In (1), Brualdi and Newman proved that (2) also holds when A is an n-square circulant with non-negative entries. In a recent conversation Dr. Newman raised the question of determining the cases of equality in (1). In the present note we answer this question.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 18 , 1966 , pp. 1085 - 1090
Copyright
Copyright © Canadian Mathematical Society 1966

References

1. Brualdi, R. A. and Newman, M., Some theorems on the permanent (to appear).Google Scholar
2. Marcus, Marvin and Mine, Henryk, Inequalities for general matrix functions, Bull. Amer. Math. Soc., 70 (1964), 308–313.Google Scholar
3. Marcus, Marvin and Mine, Henryk, Generalized matrix functions, Trans. Amer. Math. Soc. (to appear).Google Scholar
4. Marcus, Marvin and Mine, Henryk, Permanents, Amer. Math. Monthly, 72 (1965), 577–591.Google Scholar
5. Marcus, Marvin and Mine, Henryk, A survey of matrix theory and matrix inequalities (Boston, Mass., 1964).Google Scholar
6. Marcus, Marvin and Newman, Morris, Inequalities for the permanent function, Ann. Math. (2), 75 (1962), 47–62.Google Scholar