Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T01:07:39.872Z Has data issue: false hasContentIssue false
  • English
  • Français

Periods and the Asymptotics of a Diophantine Problem II

Published online by Cambridge University Press:  20 November 2018

Ben Lichtin
Ben Lichtin*
Affiliation:
University of Rochester, Rochester, NY 14627, USA
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let P(z1,…, zn) be a polynomial with positive coefficients. For positive x define 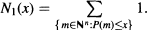A classical diophantine problem is to describe the asymptotic behavior of N1(x) as x → ∞. More generally, one can introduce a second polynomial φ satisfying the condition (0.1) Sign φ (m) is constant for all m outside at most a finite subset of ℕn.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 43 , Issue 4 , 01 August 1991 , pp. 770 - 791
Copyright
Copyright © Canadian Mathematical Society 1991

References

[Be] Bernstein, J.N., The analytic continuation of generalized functions with respect to a parameter, Functional Analysis and Applications. 6(1972), 26–40.Google Scholar
[Bro-1] Broughton, S.A., On the topology of polynomial hyper surfaces, Proc. of Symp. in Pure Math. 40 part 1 (1983), 167–178.Google Scholar
[Bro-2] Broughton, S.A.,Milnor numbers and the topology of polynomial hypersurfaces,Inv. Math. 92(1988), 217–241.Google Scholar
[Bro-3] Broughton, S.A., On the topology of polynomial hypersurfaces. Thesis at Queen's University, 1982.Google Scholar
[C-N] Cassou-Nogues, P., Valeurs aux entiers négatifs des series de Dirichlet associées à un polynome II, Amer. J. Math. 106(1985), 255–299.Google Scholar
[Da-Kh] Danilov, V. I. and Khovanski, A.G., Newton polyhedra and an algorithm for computing Hodge- Deligne numbers, Math. USSR Izves. 29(1987), 279–299.Google Scholar
[Dav] Davenport, H., Analytic methods for diophantine equations and diophantine inequalities. University of Michigan lecture notes, 1962.Google Scholar
[De] Deligne, P., Equations différentielles à Points Singuliers Réguliers. Lecture Notes in Mathematics 163, Springer-Verlag, 1970.Google Scholar
[Gin] Gindikin, S.G., Energy estimates involving the Newton polyhedron,Trans, . Moscow Math. Soc. 31(1974), 193–245.Google Scholar
[Gr] Griffithsom, P.A. results on moduli and periods of integrals on algebraic manifolds. Mimeographed Princeton U. notes, 1968.Google Scholar
[He] Herrera, M., Integration on a semi-analytic set, Bull. Soc. Math. France 94(1966), 141–180.Google Scholar
[Hoo]Hooley, C.,Orc Waring's Problem, ActaMathematica 157(1986),49–97.Google Scholar
[Ku] Kushinirenko, A., Polyèdres de Newton et nombres de Milnor, Inv. Math. 32(1976), 1–32.Google Scholar
[Li-1] Lichtin, B., GeneralizedDirichlet series and B-functions, Compositio Math. 65(1988), 81–120.Google Scholar
[Li-2] Lichtin, B., Periods and the asymptotics of a diophantine Problem, (to appear in Arkiv fur Mathematik).Google Scholar
[Li-3] Lichtin, B., The asymptotics of a lattice point problem determined by a hypoelliptic polynomial, (to appear).Google Scholar
[Lo] Lojasiewicz, S., Triangulation of semi-analytic sets, Ann. Scuola Normale sup. de Pisa 3rd series, 18 (1964), 449–474.Google Scholar
[Ma-1] Malgrange, B., Intégrales asymptotiques et monodromie, Ann. Scient. Ec. Norm. Sup. 7(1974), 405–430.Google Scholar
[Ma-2] Malgrange, B. ,Méthode de la phase stationnaire et sommation de Borel, Complex Analysis, Microlocal Calculus, and Relativistic Quantum Field Theory, Lecture Notes in Physics, Springer-Verlag 126, 1980.Google Scholar
[Nil] Nilsson, N., Some growth and ramification properties of certain integrals on algebraic manifolds, Arkiv fur Mathematik 5(1965), 463–475.Google Scholar
[P-l] Pham, F., Vanishing homologies and the n-variable saddlepoint method, Proc. Symp. in Pure Math 40, part 2 (1983), 319–334.Google Scholar
[P-2] Pham, F. ,La descente des cols par les onglets de Lefschetz avec vues sur Gauss-Manin, Astérisque 130(1985), 11–47.Google Scholar
[Sa-1] Sargos, P., Prolongement meromorphe des séries de Dirichlet associées a des fractions rationelles de plusieurs variables, Ann. Inst. Fourier 33(1984), 82–123.Google Scholar
[Sa-2] Sargos, P.,Croissance de certaines séries de Dirichlet et applications, J. fur die reine und angewandte Mathematik 367(1986), 139–154.Google Scholar
[Sa-3] Sargos, P., Series de Dirichlet et polyèdres de Newton. These d'Etat, Université de Bordeaux, 1986.Google Scholar
[Spa] Spanier, E., Algebraic Topology. McGraw-Hill, 1966.Google Scholar
[Va] Vaughn, R.C., The Hardy-Littlewood Method. Cambridge Univ. Press, 1981.Google Scholar
[Var] Varcenko, A.N., Zeta function of monodromy and Newton diagrams, Inv. Math. 37(1976), 253–262.Google Scholar
[Ve] Verdier, J.-L., Stratifications de Whitney et Théorème de Bertini-Sard, Inv. Math. 36(1976), 295–312.Google Scholar