Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T11:16:48.440Z Has data issue: false hasContentIssue false
  • English
  • Français

Periodicity in Rank 2 Graph Algebras

Published online by Cambridge University Press:  20 November 2018

Kenneth R. Davidson  and
Dilian Yang
Kenneth R. Davidson
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, ON N2L 3G1 email: [email protected]
Dilian Yang
Affiliation:
Department of Mathematics and Statistics, University of Windsor, Windsor, ON N9B 3P4 email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

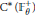Kumjian and Pask introduced an aperiodicity condition for higher rank graphs. We present a detailed analysis of when this occurs in certain rank 2 graphs. When the algebra is aperiodic, we give another proof of the simplicity of ${{\text{C}}^{*}}\left( \mathbb{F}_{\theta }^{+} \right)$. The periodic 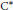${{\text{C}}^{*}}$-algebras are characterized, and it is shown that 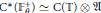${{\text{C}}^{*}}\left( \mathbb{F}_{\theta }^{+} \right)\,\simeq \,\text{C}\left( \mathbb{T} \right)\,\otimes \,\mathfrak{U}$ where 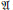$\mathfrak{A}$ is a simple 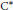${{\text{C}}^{*}}$-algebra.

Keywords

47L5547L3047L7546L05higher rank graphaperiodicity conditionsimple C*-algebraexpectation
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 6 , 01 December 2009 , pp. 1239 - 1261
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Cuntz, J., Simple C*-algebras generated by isometries. Comm. Math. Phys. 57(1977), no. 2, 173–185.Google Scholar
[2] Davidson, K. R., C-Algebras by Example. Fields Institute Monograph Series 6, American Mathematical Society, Providence, RI, 1996.Google Scholar
[3] Davidson, K. R., Power, S. C., and Yang, Dilian, Dilation theory for rank 2 graph algebras. To appear in J. Operator Theory.Google Scholar
[4] Davidson, K. R., Power, S. C., Atomic representations of rank 2 graph algebras. J. Funct. Anal. 255(2008), 819–853.Google Scholar
[5] Farthing, C., Muhly, P. S., and Yeend, T., Higher-rank graph C-algebras: an inverse semigroup and groupoid approach. Semigroup Forum 71(2005), no. 2, 159–187.Google Scholar
[6] Kribs, D.W. and Power, S. C., The analytic algebras of higher rank graphs. Math. Proc. R. Ir. Acad. 106A(2006), no. 2, 199–218.Google Scholar
[7] Kumjian, A. and Pask, D., Higher rank graph C-algebras, New York J. Math. 6(2000), 1–20.Google Scholar
[8] Pask, D., Raeburn, I., Rordam, M. and Sims, A., Rank-two graphs whose C*-algebras are direct limits of circle algebras. J. Funct. Anal. 239(2006), no. 1, 137–178.Google Scholar
[9] Power, S.C., Classifying higher rank analytic Toeplitz algebras. New York J. Math. 13(2007), 271–298 (electronic).Google Scholar
[10] Raeburn, I., Graph Algebras. CB MS Regional Converence Series in Mathematics 103. American Mathematical Society, Providence, RI, 2005.Google Scholar
[11] Raeburn, I., Sims, A. and Yeend, T., Higher-rank graphs and their C-algebras. Proc. Edinb. Math. Soc. 46(2003), no. 1, 99–115.Google Scholar
[12] Raeburn, I., Sims, A. and Yeend, T., The C*-algebras of finitely aligned higher-rank graphs. J. Funct. Anal. 213(2004), no. 1, 206–240.Google Scholar
[13] Robertson, D. I. and Sims, A., Simplicity of C*-algebras associated to higher-rank graphs. Bull. Lond. Math. Soc. 39(2007), no. 2, 337–344.Google Scholar
[14] Robertson, G. and Steger, T., Affine buildings, tiling systems and higher rank Cuntz-Krieger algebras. J. Reine Angew. Math. 513(1999), 115–144.Google Scholar
[15] Sims, A., Gauge-invariant ideals in the C*-algebras of finitely aligned higher-rank graphs. Canad. J. Math. 58(2006), no. 6, 1268–1290.Google Scholar