Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-25T21:12:12.733Z Has data issue: false hasContentIssue false
  • English
  • Français

Periodic Solutions of Non-Linear Evolution Equations in Banach Spaces

Published online by Cambridge University Press:  20 November 2018

Bui An Ton
Bui An Ton*
Affiliation:
University of British Columbia, Vancouver, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper the theory of Browder [2] and of Lions [3] on periodic solutions of non-linear evolution equations in Banach spaces is put in a more general framework so as to include the Navier-Stokes equations and their variants.

An abstract existence theorem is proved in § 1. Applications are given in § 2. The existence of periodic solutions of the Navier-Stokes equations without any restriction on the dimension of the space domain is established. Application of the abstract theorem to the following problem is given:

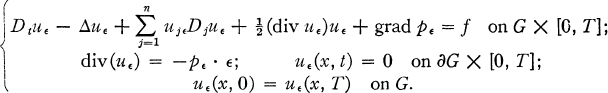
1. Let H be a Hilbert space and (., .)H the inner product in H. Let V and W be two reflexive separable Banach spaces with W ⊂ V ⊂ H. W is dense in V and V is dense in H.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 23 , Issue 1 , February 1971 , pp. 189 - 196
Copyright
Copyright © Canadian Mathematical Society 1971

References

1. Aubin, J. P., Un théorème de compacité, C. R. Acad. Sci. Paris 256 (1963), 5042–5044.Google Scholar
2. Browder, F. E., Existence of periodic solutions for nonlinear equations of evolution, Proc. Nat. Acad. Sci. U. S. A. 53 (1965), 1100–1103.Google Scholar
3. Lions, J.-L., Sur certaines équations paraboliques nonlinéaires, Bull. Soc. Math. France 93 (1965), 155–175.Google Scholar
4. Lions, J.-L., Quelques méthodes de résolution des problèmes aux limites nonlinéaires (Dunod, Paris, 1969).Google Scholar
5. Prouse, G., Soluzioni periodiche delVequazione di Navier-Stokes, Rend. Accad. Naz. Lincei 35 (1963), 443–447.Google Scholar
6. Teman, R., Une méthode d'approximation de la solution des équations de Navier-Stokes, Bull. Soc. Math. France 96 (1968), 115–152.Google Scholar
7. Ton, B. A., On strongly nonlinear parabolic equations (to appear in J. Functional Analysis).Google Scholar