Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T11:40:54.815Z Has data issue: false hasContentIssue false
  • English
  • Français

Pathological Phenomena in Denjoy–Carleman Classes

Published online by Cambridge University Press:  20 November 2018

Ethan Y. Jaffe
Ethan Y. Jaffe*
Affiliation:
Massachusetts Institute of Technology, Department of Mathematics, Building E18, Room 369, 77 Massachusetts Avenue, Cambridge, MA 02139-4307, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 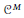${{C}^{M}}$ denote a Denjoy–Carleman class of 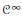${{C}^{\infty }}$ functions (for a given logarithmically-convex sequence 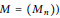$M\,=\,\left( {{M}_{n}} \right))$. We construct: (1) a function in 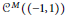${{C}^{M}}\left( \left( -1,\,1 \right) \right)$ that is nowhere in any smaller class; (2) a function on 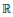$\mathbb{R}$ that is formally 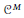${{C}^{M}}$ at every point, but not in 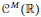${{C}^{M}}\left( \mathbb{R} \right)$; (3) (under the assumption of quasianalyticity) a smooth function on 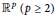${{\mathbb{R}}^{p}}\,\left( p\,\ge \,2 \right)$ that is 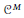${{C}^{M}}$ on every 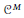${{C}^{M}}$ curve, but not in 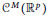${{C}^{M}}\left( {{\mathbb{R}}^{p}} \right)$.

Keywords

26E1026B3526E0530D6046E25Denjoy–Carleman classquasianalytic functionquasianalytic curvearc-quasianalytic
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 68 , Issue 1 , 01 February 2016 , pp. 88 - 108
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Acquistapace, F., Broglia, F., Bronshtein, M., Nicoara, A., and Zobin, N., Failure of the Weierstrass preparation theorem in quasi-analytic Denjoy-Carleman rings. Adv. Math. 258(2014), 397–413.http://dx.doi.Org/10.1016/j.aim.2O14.03.002 Google Scholar
[2] Baouendi, M. S., Ebenfelt, P., and Rothschild, L. P., Real submanifolds in complex space and their mappings. Princeton Mathematical Series, 47, Princeton University Press, Princeton, NJ, 1999.Google Scholar
[3] Bierstone, E. and Milman, P. D., Resolution of singularities in Denjoy–Carleman classes. Selecta Math. 10(2004), no. , 11–28.http://dx.doi.org/10.1007/s00029-004-0327-0 Google Scholar
[4] Bierstone, E., Milman, P. D, and Parusiński, A., A function which is arc-analytic but not continuous. Proc. Amer. Math. Soc. 113(1991), no. 2, 419–423.http://dx.doi.org/10.1090/S0002-9939-1991-1072083-4 Google Scholar
[5] Bierstone, E., Milman, P. D., and Valette, G., Arc-quasianalytic functions. Proc. Amer. Math. Soc, to appear. arxiv:1401.7683v1Google Scholar
[6] Boman, J., Differentiability of a function of its compositions with functions of one variable. Math. Scand. 20(1967), 249–268.Google Scholar
[7] Borel, É., Sur la généralisation du prolongement analytique. C. R. Acad. Sci. Paris 130(1900), 1115–1118.Google Scholar
[8] Chaumat, J. and Chollet, A.-M., Division par un polynôme hyperbolique. Canad. J. Math. 56(2004), no. 6, 1121–1144. http://dx.doi.org/10.4153/CJM-2004-050-1 Google Scholar
[9] Childress, C. L., Weierstrass division in quasianalytic local rings. Canad. J. Math. 28(1976), no. 5,938–953.http://dx.doi.org/10.4153/CJM-1976-091-7 Google Scholar
[10] Hörmander, L., The Analysis of linear partial differential operators. I. Springer, Berlin, 1990.Google Scholar
[11] Kriegl, A., Michor, P. W., and Rainer, A., The convenient setting for quasianalytic Denjoy–Carleman differentiable mappings. J. Funct. Anal. 261(2011), no. 7, 1799–1834.http://dx.doi.Org/10.1016/j.jfa.2O11.05.019 Google Scholar
[12] Kriegl, A., Michor, P. W., and Rainer, A., The convenient setting for non-quasianalytic Denjoy–Carleman differentiable mappings. J. Funct. Anal. 256(2009), no. 11, 3510–3544.http://dx.doi.Org/10.1016/j.jfa.2009.03.003 Google Scholar
[13] Parusiński, A. and Rolin, J.-P., A note on the Weierstrass preparation theorem in quasianalytic local rings. Canad. Math. Bull. 57(2014), no. 3, 614–620.http://dx.doi.org/10.4153/CMB-2O13-034-5 Google Scholar
[14] Rolin, J.-P., Speissegger, P., and Wilkie, A. J., Quasianalytic Denjoy–Carleman classes and o–minimality. J. Amer. Math. Soc. 16(2003), no. 4, 751–777.http://dx.doi.org/10.1090/S0894-0347-03-00427-2 Google Scholar
[15] Thilliez, V., On quasianalytic local rings. Expo. Math. 26(2008), no. 1, 1–23.http://dx.doi.org/10.1016/j.exmath.2007.04.001 Google Scholar