Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-29T00:46:22.021Z Has data issue: false hasContentIssue false
  • English
  • Français

Partial Euler Products on the Critical Line

Published online by Cambridge University Press:  20 November 2018

Keith Conrad
Keith Conrad*
Affiliation:
Department of Mathematics, University of Connecticut, Storrs, CT 06269-3009, U.S.A. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The initial version of the Birch and Swinnerton-Dyer conjecture concerned asymptotics for partial Euler products for an elliptic curve $L$-function at 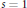$s\,=\,1$. Goldfeld later proved that these asymptotics imply the Riemann hypothesis for the $L$-function and that the constant in the asymptotics has an unexpected factor of 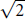$\sqrt{2}$. We extend Goldfeld's theorem to an analysis of partial Euler products for a typical $L$-function along its critical line. The general 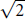$\sqrt{2}$ phenomenon is related to second moments, while the asymptotic behavior (over number fields) is proved to be equivalent to a condition that in a precise sense seems much deeper than the Riemann hypothesis. Over function fields, the Euler product asymptotics can sometimes be proved unconditionally.

Keywords

11M4111S40Euler productexplicit formulasecond moment
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 57 , Issue 2 , 01 April 2005 , pp. 267 - 297
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Ahlfors, L., Complex Analysis. McGraw-Hill, New York, 1979.Google Scholar
[2] Birch, B., Conjectures concerning elliptic curves. Proc. Symp. Pure Math. 8(1965), 106–112.Google Scholar
[3] Bochner, S., On Riemann's functional equation with multiple Gamma factors. Ann. of Math. 67(1958), 29–41.Google Scholar
[4] Breuil, C., Conrad, B., Diamond, F. and Taylor, R., On the modularity of elliptic curves over Q: wild 3-adic exercises. J. Amer.Math. Soc. 14(2001), 843–939.Google Scholar
[5] Brock, B. W. and Granville, A., More points than expected on curves over finite field extensions. Finite Fields Appl. 7(2001), 70–91.Google Scholar
[6] Buhler, J. P., Gross, B. H. and Zagier, D. B., On the conjecture of Birch and Swinnerton-Dyer for an elliptic curve of rank 3. Math. Comp. 44(1985), 473–481.Google Scholar
[7] Conrad, B., Diamond, F. and Taylor, R.,Modularity of certain potentially Barsotti-Tate Galois representations. J. Amer.Math. Soc. 12(1999), 521–567.Google Scholar
[8] Conrey, J. B. and Ghosh, A., On the Selberg class of Dirichlet series: small degrees. Duke Math. J. 72(1993), 673–693.Google Scholar
[9] Deligne, P., La conjecture de Weil, II. Inst. Hautes Études Sci. Publ. Math. 52(1980), 137–252.Google Scholar
[10] Diamond, F., On deformation rings and Hecke rings. Ann. of Math. 144(1996), 137–166.Google Scholar
[11] Gallagher, P. X., Some consequences of the Riemann hypothesis. Acta Arith. 37(1980), 339–343.Google Scholar
[12] Goldfeld, D., Sur les produits eulériens attachés aux courbes elliptiques. Acad, C. R.. Sci. Paris Sér. I Math. 294(1982), 471–474.Google Scholar
[13] Hardy, G. H., A note on the continuity or discontinuity of a function defined by an infinite product. Collected Papers Vol. VI, Oxford, 1974.Google Scholar
[14] Katz, N. M., Frobenius-Schur indicator and the ubiquity of Brock-Granville quadratic excess. Finite Fields Appl. 7(2001), 45–69.Google Scholar
[15] Kuo, W. and Murty, M. R., On a conjecture of Birch and Swinnerton-Dyer. Canad. J. Math. 57(2005), 328–337.Google Scholar
[16] Montgomery, H., The zeta function and prime numbers. In: Proceedings of the Queen's Number Theory Conference, 1979, Queen's University, Kingston, 1980.Google Scholar
[17] Moreno, C. J. and Shahidi, F., The Fourth Moment of Ramanujan τ -function. Inv.Math. 266(1983), 233–239.Google Scholar
[18] Murty, V. K., On the Sato-Tate conjecture. In: Number Theory related to Fermat's Last Theorem, (Koblitz, N. ed.), Birkhäuser, Boston, 1982.Google Scholar
[19] Murty, V. K., Modular elliptic curves. In: Seminar on Fermat's Last Theorem, (Murty, V. K., ed.), Amer. Math. Soc., Providence, RI, 1995, pp. 1–38.Google Scholar
[20] Nagao, K., Construction of high-rank elliptic curves. Kobe J. Math. 11(1994), 211–219.Google Scholar
[21] Rosen, M., A generalization of Mertens’ theorem. Ramanujan, J. Math. Soc. 14(1999), 1–19.Google Scholar
[22] Rubin, K. and Silverberg, A., Ranks of elliptic curves. Bull. Amer. Math. Soc. 39(2002), 455–474.Google Scholar
[23] Rubinstein, M. and Sarnak, P., Chebyshev's bias. Experiment. Math. 3(1994), 173–197.Google Scholar
[24] Rudnick, Z. and Sarnak, P., Zeros of principal L-functions and random matrix theory. Duke Math. J. 81(1996) 269–322.Google Scholar
[25] Selberg, A., Old and new conjectures and results about a class of Dirichlet series. In: Proceedings of the Amalfi conference on analytic number theory, (Bombieri, E. et al. eds.), Universit à di Salerno, Salerni, 1982, pp. 367–385.Google Scholar
[26] Serre, J-P., Quelques applications du théorème de densité de Chebotarev. Inst. Hautes Études Sci. Publ. Math. 54(1981), 123–201.Google Scholar
[27] Shimura, G., On the holomorphy of certain Dirichlet series. Proc. LondonMath. Soc. 31(1975), 79–98.Google Scholar
[28] Ulmer, D., Elliptic curves with large rank over function fields. Ann. of Math. 155(2002), 295–315.Google Scholar
[29] Vignéras, M-F., Facteurs Gamma et équations fonctionnelles. In: Modular functions of one variable, VI, (Serre, J-P. and Zagier, D., eds.), Lecture Notes in Math. 627, Springer–Verlag, Berlin, 1977, pp. 79–103.Google Scholar
[30] Wiles, A., Modular elliptic curves and Fermat's last theorem. Ann. of Math. 141(1995), 443–551.Google Scholar
[31] Wintner, A., A factorization of the densities of the ideals in algebraic number fields. Amer. J. Math. 68(1946), 273–284.Google Scholar