No CrossRef data available.
Article contents
Partial ∗-Automorphisms, Normalizers, and Submodules in Monotone Complete C*-Algebras
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
For monotone complete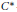 
${{C}^{*}}$-algebras 
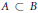$A\subset B$ with 
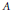$A$ contained in 
$B$ as a monotone closed 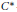${{C}^{*}}$-subalgebra, the relation 
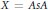$X=AsA$ gives a bijection between the set of all monotone closed linear subspaces 
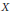$X$ of $B$ such that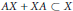 
$AX+XA\subset X$ and 
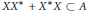$X{{X}^{*}}+{{X}^{*}}X\subset A$ and a set of certain partial isometries 
$s$ in the “normalizer” of 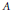$A$ in $B$, and similarly for the map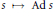 
$s\mapsto \text{Ad }s$ between the latter set and a set of certain “partial 
$*$-automorphisms” of 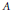$A$. We introduce natural inverse semigroup structures in the set of such 
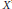$X$'s and the set of partial $*$-automorphisms of 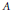$A$, modulo a certain relation, so that the composition of these maps induces an inverse semigroup homomorphism between them. For a large enough $B$ the homomorphism becomes surjective and all the partial $*$-automorphisms of 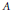$A$ are realized via partial isometries in $B$. In particular, the inverse semigroup associated with a type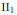 
$\text{I}{{\text{I}}_{1}}$ von Neumann factor, modulo the outer automorphism group, can be viewed as the fundamental group of the factor. We also consider the 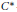${{C}^{*}}$-algebra version of these results.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2006
References
[1]
Berberian, S. K.,
Baer *-Rings.
Grundlehren der Mathematischen Wissenschaften
195, Springer-Verlag, New York, 1972.Google Scholar
[2]
Blackadar, B., K-Theory for Operator Algebras.
Mathematical Sciences Research Institute Publications
5, Springer-Verlag, New York, 1986.Google Scholar
[3]
Brown, L. G., Green, P., and Rieffel, M. A., Stable isomorphism and strong Morita equivalence of C*-algebras. Pacific J. Math.
71(1977), no. 2, 349–363.Google Scholar
[4]
Cuntz, J., Simple C*-algebras generated by isometries. Comm. Math. Phys.
57(1977), no. 2, 173–185.Google Scholar
[5]
Dixmier, J., Sur certains espaces considérés par M. H. Stone. Summa Brasil. Math.
2(1951), 151–182.Google Scholar
[6]
Dixmier, J., Sous-anneaux abélian maximaux dans les factuers de type fini. Ann. of Math.
59(1954), 279–286.Google Scholar
[7]
Exel, R., Circle actions on C*-algebras, partial automorphisms, and a generalized Pimsner-Voiculescu exact sequence. J. Funct. Anal.
122(1994), no. 2, 361–401.Google Scholar
[8]
Exel, R., Twisted partial actions: a classification of regular C*-algebra bundles. Proc. London Math. Soc.(3)
74(1997), no. 2, 417–443.Google Scholar
[10]
Hamana, M., Tensor products for monotone complete C*-algebras. I. Japan. J. Math. (N.S.)
8(1982), no. 2, 259–283.Google Scholar
[11]
Hamana, M., Dynamical systems based on monotone complete C*-algebras.
In: Current Topics in Operator Algebras. World Scientific. Publishing, River Edge, NJ, 1991, pp. 282–296.Google Scholar
[12]
Hamana, M., Modules over monotone complete C*-algebras. Intern. J. Math.
3(1992), no. 2, 185–204.Google Scholar
[13]
Hamana, M., Infinite. σ-finite, non-W*, AW*-factors. Internat. J. Math.
12(2001), no. 1, 81–95.Google Scholar
[14]
Hamana, M., Coactions of discrete groups on monotone complete C*-algebras, in preparation.Google Scholar
[15]
Hewitt, E. and Ross, K. A., Abstract harmonic analysis. II.
Grundlehren der Mathematischen Wissenschaften
152, Springer-Verlag, New York, 1970.Google Scholar
[17]
Kadison, R. V., Operator algebras with a faithful weakly-closed representation. Ann. of Math.
64(1956), 175–181.Google Scholar
[18]
Kadison, R V. and Pedersen, G. K., Equivalence in operator algebras.
Math. Scand.
27(1970), 205–222.Google Scholar
[20]
Lawson, M. V., Inverse Semigroups. The Theory of Partial Symmetries.
World Scientific Publishing, River Edge, NJ, 1998.Google Scholar
[21]
Murray, F. J. and von Neumann, J., Rings of operators. IV. Ann. of Math.
44(1943), 716–808.Google Scholar
[22]
Nakagami, Y. and Takesaki, M., Duality for crossed products of von Neumann algebras.
Lecture Notes in Mathematics
731, Springer-Verlag, Berlin, 1979.Google Scholar
[23]
Ozawa, M., Nonuniqueness of the cardinality attached to homogeneous AW*-algebras. Proc. Amer. Math. Soc.
93(1985), no. 4, 681–684.Google Scholar
[24]
Paterson, A. L. T., Groupoids, Inverse Semigroups, and Their Operator Algebras.
Progress in Math.
170, Birkhäuser Boston, Boston, MA, 1999.Google Scholar
[25]
Pedersen, G. K., C*-Algebras and Their Automorphism Groups.
London Mathematical Society Monographs
14, Academic Press, London, 1979.Google Scholar
[26]
Power, S. C., Limit Algebras: An Introduction to Subalgebras of C*-Algebras.
Pitman Research Notes in Mathematics
278, Longman Scientific and Technical, Harlow, 1992.Google Scholar
[27]
Reid, G. A., A generalisation ofW*-algebras. Pacific J. Math.
15(1965), 1019–1026.Google Scholar
[28]
Rieffel, M. A., Unitary representations of group extensions; an algebraic approach to the theory of Mackey and Blattner.
In: Studies in Analysis, Adv. in Math. Suppl. Stud.
4, Academic Press, New York, 1979, pp. 43–82.Google Scholar
[29]
Saitō, K. and Wright, J. D. M., All AW*-factors are normal. J. London Math. Soc.(2)
44(1991), no. 1, 143–154.Google Scholar
[30]
Sakai, S., C*-algebras and W*-algebras.
Ergebnisse der Mathematik und ihrer Grenzgebiete
60, Springer-Verlag, New York, 1971.Google Scholar
[31]
Takesaki, M., The structure of a von Neumann algebra with a homogeneous periodic state. Acta Math.
131(1973), 79–121.Google Scholar
[33]
Tomiyama, J., Tensor products and projections of norm one in von Neumann algebras. Lecture Notes, University of Copenhagen, 1970.Google Scholar
[34]
Wright, J. D. M., On some problems of Kaplansky in the theory of rings of operators. Math. Z.
172(1980), no. 2, 131–141.Google Scholar
[35]
Youngson, M. A., Completely contractive projections on C*-algebras. Quart. J. Math. Oxford
34(1983), 507-511.Google Scholar
[36]
Zettl, H. H., A characterization of ternary rings of operators. Adv. in Math.
48(1983), no. 2, 117–143.Google Scholar
You have
Access