Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T01:09:21.180Z Has data issue: false hasContentIssue false
  • English
  • Français

Parametrizing Fuchsian Subgroups of the Bianchi Groups

Published online by Cambridge University Press:  20 November 2018

C. Maclachlan  and
A. W. Reid
C. Maclachlan
Affiliation:
Department of Mathematics, University of Aberdeen, Dunbar Street, Aberdeen AB9 2TY, Scotland, U.K.
A. W. Reid
Affiliation:
Department of Mathematics, The Ohio State University, 231 West 18th Avenue, Columbus, OH 43210, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

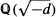Let dbe a positive square-free integer and let Od denote the ring of integers in . The groups PSL2(Od) are collectively known as the Bianchi groups and have been widely studied from the viewpoints of group theory, number theory and low-dimensional topology. The interest of the present article is in geometric Fuchsian subgroups of the groups PSL2(Od). Clearly PSL2 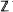is such a subgroup; however results of [18], [19] show that the Bianchi groups are rich in Fuchsian subgroups.

Keywords

11F0620H10
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 43 , Issue 1 , 01 February 1991 , pp. 158 - 181
Copyright
Copyright © Canadian Mathematical Society 1991

References

1. Beardon, A.F., The Geometry of discrete groups, Graduate texts in Math 91, Springer Verlag (1983).Google Scholar
2. Borel, A., Commensurability classes and volumes of hyperbolic 3-manifolds, Ann. Sc. Norm. Sup. Pisa 8(1981), 1–33.Google Scholar
3. Borel, A. and Harish-Chandra, Arithmetic subgroups of algebraic groups, Ann of Math. 75(1962), 485–535.Google Scholar
4. Cassete, J.W.S., Rational Quadratic Forms. Academic Press, London (1978).Google Scholar
5. Chinburg, T. and Friedman, E., Torsion in arithmetic subgroups of forms 0/PGL2. (Preprint).Google Scholar
6. Elstrodt, J., Grunewald, F. and Mennicke, J., A Survey of some aspects of Siegel's theory, Manuscript, Bielefeld (1985).Google Scholar
7. Fine, B., The structure of?SL2(R), Ann. of Math. Studies 79(1974), 145–170.Google Scholar
8. Fine, B., Fuchsian subgroups of the Picard group, Can. J. Math 28(1976), 481–486.Google Scholar
9. Fine, B., Fuchsian embeddings in the Bianchi groups, Can. J. Math. 39(1987), 1434–1445.Google Scholar
10. Fine, B. and Frohman, C., Some amalgam structures for Bianchi groups, Proc. A.M.S. 102(1988), 221–229.Google Scholar
11. Fine, B. and Newman, M., Normal subgroup structure of the Picard group, Trans. A.M.S. 302(1987), 769- 786.Google Scholar
12. Greenberg, L., On a theorem of Ahlfors and conjugate subgroups of Kleinian groups, Amer.J. Math. 89(1967), 56–68.Google Scholar
13. Harding, S., Ph.D. thesis. Univ. of Southampton, 1985.Google Scholar
14. Helling, H., Bestimmung der Kommersurabilitätsklasse der Hilbertschen Modulgruppe, Math. Zeit. 92(1966), 269–280.Google Scholar
15. Hoare, A.H.M., Karass, A. and Solitar, D., Subgroups of infinite index in Fuchsian groups, Math. Zeit 125(1972), 59–69.Google Scholar
16. Humbert, P., Reduction de formes quadratiques dans un corps algébrique fini, Comment. Math. Helv. 23(1949), 50–63.Google Scholar
17. Lozano, M.T., Arcbodies, Math. Proc. Camb. Phil. Soc. 94(1983), 253–260.Google Scholar
18. Maclachlan, C., Fuchsian subgroups of the groups PSL2(Od). In Low-Dimensional Topology and Kleinian groups, ed. D. B. A. Epstein. L.M.S. Lecture note series 112(1986), 305–311.Google Scholar
19. Maclachlan, C. and Reid, A.W., Commensurability classes of arithmetic Kleinian groups and their Fuchsian subgroups, Math. Proc. Camb. Phil. Soc. 102(1987), 251–258.Google Scholar
20. Maclachlan, C. and Reid, A.W., Maclachlan and Reid, A.W., The arithmetic structure of tetrahedral groups of hyperbolic isometries, Mathematika 36(1989).Google Scholar
21. Reid, A.W., Ph.D. thesis, Univ. of Aberdeen, 1987.Google Scholar
22. Maclachlan, and Reid, A.W., Totally geodesic surfaces in hyperbolic 3-manifolds, to appear in Proc. Edinburgh Math. Soc.Google Scholar
23. Rohlfs, J., On the cuspidal cohomology of the Bianchi modular groups, Math. Zeit. 188(1985), 253–269.Google Scholar
24. Scott, G.P., Subgroups of surface groups are almost geometric, J. Lond. Math. Soc. (2) 17(1978), 555–565.Google Scholar
25. Siegel, C.L., Über die analytische theorie der quadratischen formen I, II, III, Ann. of Math. 36(1935),527- 606. Ibid. 37(1936), 230–267. Ibid. 38(1937), 212–291.Google Scholar
26. Singerman, D., Subgroups of Fuchsian groups and finite permutation groups, Bull. London Math. Soc. 2(1970), 319–323.Google Scholar
27. Takeuchi, K., On some discrete subgroups of SL2( ), J. Fac. Sci. Univ. Tokyo Sec. 116(1969), 97–100.Google Scholar
28. Takeuchi, K., Commensurability classes of arithmetic triangle groups, J. Fac. Sci. Univ. Tokyo Sec. 124(1977), 201–212.Google Scholar
29. Thurston, W.P., The geometry and topology of 3-manifolds. Lecture notes, Princeton Univ., 1978.Google Scholar
30. Vignéras, M.-F., Arithmétique des Algèbres de Quaternions, L.N.M. 800, Springer-Verlag, 1980.Google Scholar
31. Wielenberg, N.J., The structure of certain subgroups of the Picard group, Math. Proc. Camb. Phil. Soc. 84(1978), 427–436.Google Scholar
32. Zimmert, R., Zür SL2 der ganzen Zahlen eines imaginar-quadratischen Zahlkorpers, Invent. Math. 19(1973), 73–82.Google Scholar