Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T01:34:09.163Z Has data issue: false hasContentIssue false
  • English
  • Français

Parabolic Subgroups with Abelian Unipotent Radical as a Testing Site for Invariant Theory

Published online by Cambridge University Press:  20 November 2018

Dmitri I. Panyushev
Dmitri I. Panyushev*
Affiliation:
ul. Akad. Anokhina, d.30, kor.1, kv.7, Moscow 117602, Russia email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $L$ be a simple algebraic group and $P$ a parabolic subgroup with Abelian unipotent radical 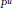${{P}^{u}}$ . Many familiar varieties (determinantal varieties, their symmetric and skew-symmetric analogues) arise as closures of $P$-orbits in 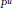${{P}^{u}}$ . We give a unified invariant-theoretic treatment of various properties of these orbit closures. We also describe the closures of the conormal bundles of these orbits as the irreducible components of some commuting variety and show that the polynomial algebra 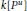$k[{{P}^{u}}]$ is a free module over the algebra of covariants.

Keywords

14L3013A50
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 51 , Issue 3 , 01 June 1999 , pp. 616 - 635
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Brion, M., Invariants d’un sous-groupe unipotent maximal d’un groupe semi-simple. Ann. Inst. Fourier. 33 (1983), 1–27.Google Scholar
[2] Johnson, K., On a ring of invariant polynomials on a Hermitian symmetric space. J. Algebra. 67 (1980), 72–81.Google Scholar
[3] Kempf, G., On the collapsing of homogeneous bundles. Invent.Math.. 37 (1976), 229–239.Google Scholar
[4] Kostant, B. and Rallis, S., Orbits and representations associated with symmetric spaces. Amer. J. Math.. 93 (1971), 753–809.Google Scholar
[5] Muller, I., Rubenthaler, H. and Schiffmann, G., Structure des espaces préhomogènes associés a certaines algèbres de Lie graduées. Math. Ann.. 274 (1986), 95–123.Google Scholar
[6] Panyushev, D., Orbits of maximal dimension of solvable subgroups of reductive algebraic groups and reduction for U-invariants. Mat. Sb.. 132 (1987), 371–382. (Russian); English transl.: Math. USSR-Sb. 60 (1988), 365-375.Google Scholar
[7] Panyushev, D., A restriction theorem and the Poincaré series forU-invariants. Math. Ann.. 301 (1995), 655–675.Google Scholar
[8] Panyushev, D., On deformation method in Invariant Theory. Ann. Inst. Fourier. 47 (1997), 985–1011.Google Scholar
[9] Panyushev, D., On the conormal bundle of a G-stable subvariety. Manuscripta Math. 99 (1999), to appear.Google Scholar
[10] Popov, V. L., Contractions of actions of reductive algebraic groups. Mat. Sb.. 130 (1986), 310–334. (Russian); English transl.: Math. USSR Sb. 58 (1987), 311-335.Google Scholar
[11] Pyasetskii, V. S., Linear Lie groups acting with finitely many orbits. Funktsional. Anal. i Prilozhen. (4). 9 (1975), 85–86. (Russian); English transl.: Funct. Anal. Appl. 9 (1975), 351-353.Google Scholar
[12] Richardson, R., Röhrle, G. and Steinberg, R., Parabolic subgroups with Abelian unipotent radical. Invent.Math.. 110 (1992), 649–671.Google Scholar
[13] Schmid, W., Die randwerte holomorpher Funktionen auf hermitesch symmetrischen Räumen. Invent. Math.. 9 (1969), 61–80.Google Scholar
[14] Springer, T. A. and Steinberg, R., Conjugacy classes. In: Seminar on algebraic groups and related finite groups, Lecture Notes in Math. 131, Springer-Verlag, Berlin-Heidelberg-New York, 1970, 167–266.Google Scholar
[15] Vinberg, E. B., The Weyl group of a graded Lie algebra. Izv. Akad. Nauk SSSR Ser. Mat.. 40 (1976), 488–526. (Russian); English transl.: Math. USSR-Izv. 10 (1976), 463-495.Google Scholar
[16] Vinberg, E. B. and Popov, V. L., On a class of quasihomogeneous affine varieties. Izv. Akad. Nauk SSSR. Ser. Mat.. 36 (1972), 749–764.Google Scholar