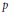No CrossRef data available.
Article contents
Pair Correlation of Squares in 
$p$-Adic Fields
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let 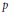$p$ be an odd prime number, 
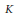$K$ a 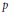$p$-adic field of degree 
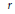$r$ over 
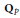${{\mathbf{Q}}_{p}}$, 
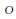$O$ the ring of integers in 
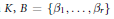$K,\,B\,=\,\{{{\beta }_{1}},\ldots .{{\beta }_{r}}\}$ an integral basis of 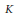$K$ over 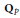${{\mathbf{Q}}_{p}}$, 
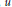$u$ a unit in 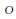$O$ and consider sets of the form 
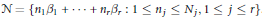$N\,=\,\{{{n}_{1}}{{\beta }_{1}}\,+\ldots +\,{{n}_{r}}{{\beta }_{r}}\,:\,1\,\le \,{{n}_{j}}\,\le \,{{N}_{j}},\,1\,\le \,j\,\le \,r\}$. We show under certain growth conditions that the pair correlation of 
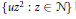$\{u{{z}^{2}}\,:\,z\,\in N\}$ becomes Poissonian.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2003
References
[1]
Boca, F. and Zaharescu, A., Pair correlation of values of rational functions (mod p). Duke Math. J. (2) 105 (2000), 267–307.Google Scholar
[2]
Davenport, H., On a principle of Lipschitz. J. LondonMath. Soc. 26 (1951), 179–183. Corrigendum: On a principle of Lipschitz, J. LondonMath. Soc. 39(1964), 580.Google Scholar
[4]
Kurlberg, P., The distribution of spacings between quadratic residues. II. Israel J. Math. (A) 120 (2000), 205–224.Google Scholar
[5]
Kurlberg, P. and Rudnick, Z., The distribution of spacings between quadratic residues. Duke Math. J. 100 (1999), 211–242.Google Scholar
[6]
Rudnick, Z. and Sarnak, P., The pair correlation function of fractional parts of polynomials. Comm. Math. Phys. (1) 194 (1998), 61–70.Google Scholar
[7]
Rudnick, Z., Sarnak, P. and Zaharescu, A., The distribution of spacings between the fractional parts of n2α. Invent.Math. (1) 145 (2001), 37–57.Google Scholar
[8]
Salie´, S., U¨ber die Kloostermanschen Summen S(u, v, q). Math. Z. 34 (1931), 91–109.Google Scholar
You have
Access