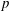Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-24T01:54:14.789Z Has data issue: false hasContentIssue false
  • English
  • Français

$p$-adic 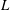$L$-functions for 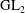$\text{GL}_{2}$

Part of: Zeta and $L$-functions: analytic theory Discontinuous groups and automorphic forms Algebraic number theory: local and $p$-adic fields

Published online by Cambridge University Press:  07 January 2019

Daniel Barrera Salazar  and
Chris Williams
Daniel Barrera Salazar
Affiliation:
Universitat Politécnica de Catalunya, Campus Nord, Calle Jordi Girona, 1-3, 08034 Barcelona, Spain Email: [email protected]
Chris Williams
Affiliation:
Mathematics Department, Imperial College London, South Kensington Campus, London, SW7 2AZ, UK Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Since Rob Pollack and Glenn Stevens used overconvergent modular symbols to construct 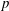$p$-adic 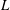$L$-functions for non-critical slope rational modular forms, the theory has been extended to construct 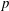$p$-adic 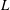$L$-functions for non-critical slope automorphic forms over totally real and imaginary quadratic fields by the first and second authors, respectively. In this paper, we give an analogous construction over a general number field. In particular, we start by proving a control theorem stating that the specialisation map from overconvergent to classical modular symbols is an isomorphism on the small slope subspace. We then show that if one takes the modular symbol attached to a small slope cuspidal eigenform, then one can construct a ray class distribution from the corresponding overconvergent symbol, which moreover interpolates critical values of the 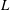$L$-function of the eigenform. We prove that this distribution is independent of the choices made in its construction. We define the 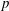$p$-adic 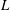$L$-function of the eigenform to be this distribution.

Keywords

automorphic formGL(2)p-adic L-functionL-functionmodular symboloverconvergentcohomologyautomorphic cyclecontrol theoremL-valuedistribution

MSC classification

Primary: 11F41: Automorphic forms on $(2)$; Hilbert and Hilbert-Siegel modular groups and their modular and automorphic forms; Hilbert modular surfaces
Secondary: 11F67: Special values of automorphic $L$-series, periods of modular forms, cohomology, modular symbols 11F85: $p$-adic theory, local fields 11S40: Zeta functions and $L$-functions 11M41: Other Dirichlet series and zeta functions
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 5 , October 2019 , pp. 1019 - 1059
Copyright
© Canadian Mathematical Society 2018 

Footnotes

Author D. B. S. was funded by the Centre de Recherches Mathématiques in Montreal and the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 682152). Author C. W. was supported by an EPSRC DTG doctoral grant at the University of Warwick.

References

Bergdall, John and Hansen, David, On p-adic L-functions for Hilbert modular forms. 2017. arxiv:1710.05324.Google Scholar
Barrera Salazar, Daniel, Cohomologie surconvergente des variétés modulaires de Hilbert et fonctions L p-adiques. Ph.D. thesis, Université Lille, 2013. http://ori.univ-lille1.fr/notice/view/univ-lille1-ori-182045.Google Scholar
Barrera Salazar, Daniel, Overconvergent cohomology of Hilbert modular varieties and p-adic L-functions . Ann. I. Fourier (2015), To appear.Google Scholar
Castella, Francesc, On the p-part of the Birch-Swinnerton-Dyer formula for multiplicative primes . Camb. J. Math. (2017), To appear.Google Scholar
Castella, Francesc, Çiperiani, Mirela, Skinner, Christopher, and Sprung, Florian, On the Iwasawa main conjectures for modular forms at non-ordinary primes. https://web.math.princeton.edu/∼fcabello/Wach.pdf.Google Scholar
Colmez, Pierre, Fonctions d’une variable p-adique, Asterisque no. 330, (2010), 13–59.Google Scholar
Deligne, Pierre, Les constantes des equations fonctionelles des functions L , Modular functions of one variable, II (Proc. Internat. Summer School, Univ. Antwerp), Lecture Notes in Math., vol. 349, 1972.Google Scholar
Deppe, Holger, p-adic L-functions of automorphic forms and exceptional zeros . Doc. Math. 21(2016), 689–734.Google Scholar
Dimitrov, Mladen, Galois representations modulo p and cohomology of Hilbert modular varieties . Ann, Sci. École Norm. Sup. (4) 38(2005), 505–551. https://doi.org/10.1016/j.ansens.2005.03.005.Google Scholar
Dimitrov, Mladen, Automorphic symbols, p-adic L-functions and ordinary cohomology of Hilbert modular varieties . Amer. J. Math 135(2013), 1117–1155. https://doi.org/10.1353/ajm.2013.0035.Google Scholar
Disegni, Daniel, On the p-adic Birch and Swinnerton-Dyer conjecture for elliptic curves over number fields . Kyoto J. Math., to appear.Google Scholar
Haran, Shai, p-adic L-functions for modular forms . Comp. Math. 62(1987), 31–46.Google Scholar
Hida, Haruzo, On p-adic Hecke algebras for GL2 over totally real fields . Ann. of Math. 128(1988), 295–384. https://doi.org/10.2307/1971444.Google Scholar
Hida, Haruzo, p-ordinary cohomology groups for SL2 over number fields . Duke Math. J. 69(1993), 259–314. https://doi.org/10.1215/S0012-7094-93-06914-1.Google Scholar
Hida, Haruzo, On the critical values of L-functions of GL(2) and GL(2) × GL(2) . Duke Math. J. 74(1994), 432–529. https://doi.org/10.1215/S0012-7094-94-07417-6.Google Scholar
Jetchev, Dimitar, Skinner, Christopher, and Wan, Xin, The Birch and Swinnerton-Dyer formula for elliptic curves of analytic rank one . Camb. J. Math. 5(2017), 369–434. https://doi.org/10.4310/CJM.2017.v5.n3.a2.Google Scholar
Loeffler, David, P-adic integration on ray class groups and non-ordinary p-adic L-functions . In: Iwasawa 2012 . Contrib. Math. Comput. Sci., 7. Springer, Heidelberg, 2014, pp. 357–378.Google Scholar
Mazur, Barry and Swinnerton-Dyer, Peter, Arithmetic of Weil curves . Invent. Math. 25(1974), 1–61. https://doi.org/10.1007/BF01389997.Google Scholar
Mazur, Barry, Tate, John, and Teitelbaum, Jeremy, On p-adic analogues of the Birch and Swinnerton-Dyer conjecture . Invent. Math. 84(1986), 1–48. https://doi.org/10.1007/BF01388731.Google Scholar
Narkiewicz, Władysław, Elementary and analytic theory of algebraic numbers . Third edition. Springer-Verlag, Berlin, 2004.Google Scholar
Pollack, Robert and Stevens, Glenn, Overconvergent modular symbols and p-adic L-functions . Ann. Sci. École Norm. Sup. 44(2011), 1–42. https://doi.org/10.24033/asens.2139.Google Scholar
Pollack, Robert and Stevens, Glenn, Critical slope p-adic L-functions . J. Lond. Math. Soc. 87(2013), 428–452. https://doi.org/10.1112/jlms/jds057.Google Scholar
Schneider, Peter, Nonarchimedean functional analysis . Springer Monographs in Mathematics. Springer-Verlag, Berlin, 2002.Google Scholar
Shimura, Goro, On the periods of modular forms . Math. Ann. 229(1977), 211–221. https://doi.org/10.1007/BF01391466.Google Scholar
Shimura, Goro, The special values of the zeta functions associated with Hilbert modular forms . Duke Math. J. 45(1978), 637–679. https://doi.org/10.1215/S0012-7094-78-04529-5.Google Scholar
Stevens, Glenn, Rigid analytic modular symbols. Preprint, 1994. http://math.bu.edu/people/ghs/research.d/RigidSymbs.pdf.Google Scholar
Skinner, Christopher and Urban, Eric, The Iwasawa main conjectures for GL(2) . Invent. Math. 195(2014), 1–277. https://doi.org/10.1007/s00222-013-0448-1.Google Scholar
Tate, John, Number theoretic background . In: Automorphic forms, representations and L-functions . Proc. Sympos. Pure Math. XXXIII. Amer. Math. Soc., Providence, RI, 1979, pp. 3–26.Google Scholar
Urban, Eric, Eigenvarieties for reductive groups . Ann. of Math. 174(2011), 1695–1784. https://doi.org/10.4007/annals.2011.174.3.7.Google Scholar
‘ Weil, André, On a certain type of characters of the idele-class group of an algebraic number-field . In: Proceedings of the international symposium on algebraic number theory . Science Council of Japan, Tokyo, 1956, pp. 1–7.Google Scholar
Weil, André, Dirichlet series and automorphic forms , Lecture Notes in Math., vol. 189, Springer-Verlag, Berlin, Heidelberg, 1971.Google Scholar
Williams, Chris, Overconvergent modular symbols over number fields. Ph.D. thesis, University of Warwick, 2016.Google Scholar
Williams, Chris, P-adic L-functions of Bianchi modular forms . Proc. Lond. Math. Soc. 114(2017), 614–656. https://doi.org/10.1112/plms.12020.Google Scholar