Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T00:48:18.206Z Has data issue: false hasContentIssue false
  • English
  • Français

p-Adic Eigen-Eunctions for Kubert Distributions

Published online by Cambridge University Press:  20 November 2018

Neal Koblitz
Neal Koblitz*
Affiliation:
University of Washington, Seattle, Washington
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Functions on R (or on R/Z, or Q/Z, or the interval (0,1)) which satisfy the identity

1.1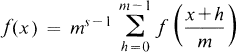

for positive integers m and fixed complex s, appear in several branches of mathematics (see [8], p. 65-68). They have recently been studied systematically by Kubert [6] and Milnor [12]. Milnor showed that for each complex s there is a one-dimensional space of even functions and a one-dimensional space of odd functions which satisfy (1.1). These functions can be expressed in terms of either the Hurwitz partial zeta-function or the polylogarithm functions.

My purpose is to prove an analogous theorem for p-adic functions. The p-adic analog is slightly more general; it allows for a Dirichlet character χ0(m) in front of ms–l in (1.1). The functions satisfying (1.1) turn out to be p-adic “partial Dirichlet L-functions”, functions of two p-adic variables (x, s) and one character variable χ0 which specialize to partial zeta-functions when χ0 is trivial and to Kubota-Leopoldt L-functions when x = 0.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 35 , Issue 4 , 01 August 1983 , pp. 674 - 686
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. Diamond, J., The p-adic log gamma function and p-adic Eider constants, Trans. A.M.S. 233 (1977), 321–337.Google Scholar
2. Diamond, J., On the values of p-adic L-functions at positive integers, Acta Arith. 35(1979), 223–237.Google Scholar
3. Iwasawa, K., Lectures on p-adic L-functions (Princeton Univ. Press, 1972).CrossRefGoogle Scholar
4. Koblitz, N., A new proof of certain formulas for p-adic L-functions, Duke Math. J. 46 (1979), 455–468.Google Scholar
5. Koblitz, N., p-adic analysis: A short course on recent work (Cambridge Univ. Press, 1980).CrossRefGoogle Scholar
6. Kubert, D., The universal ordinary distribution, Bull. Soc. Math. France 707(1979), 179–202.Google Scholar
7. Kubota, T. and Leopoldt, H. W., Eine p-adische theorie der zetawerte I, J. Reine und angew. Math. 214/215(1964), 328–339.Google Scholar
8. Lang, S., Cyclotomic fields (Springer-Verlag, 1978).CrossRefGoogle Scholar
9. Lang, S., Cyclotomic fields, vol. 2 (Springer-Verlag, 1980).CrossRefGoogle Scholar
10. Manin, Ju. I., Periods of cusp forms and p-adic Hecke series, Mat. Sbornik 93(1973), 378–401.Google Scholar
11. Mazur, B., Analysep-adique, Bourbaki report (unpublished) (1972).Google Scholar
12. Milnor, J., On poly logarithms, Hurwitz zeta functions, and the Kubert identities, preprint.Google Scholar
13. Morita, Y., A p-adic analogue of the Γ-function, J. Fac. Sci. Univ. Tokyo 22(1975), 255–266.Google Scholar
14. Visik, M. M., Non-archimedean measures connected with Dirichlet series, Mat. Sbornik 99(1976), 248–260.Google Scholar
15. Visik, M. M., On applications of the Shnirelman integral in non-archimedean analysis, Uspehi Mat. Nauk 34 (1919) 223–224.Google Scholar