Published online by Cambridge University Press: 20 November 2018
Consider the n-th order (n ≥ 1 ) neutral differential equation 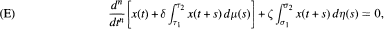 where
where 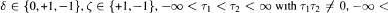 σ1 < σ 2 < ∞ and μ and η are increasing real-valued functions on [Ƭ1, Ƭ2] and [σ1, σ2] respectively. The function μ is assumed to be not constant on [Ƭ1, Ƭ2] and [Ƭ1, Ƭ2] for every Ƭ ∈ (Ƭ1, Ƭ2) similarly, for each σ ∈ (σ1, σ2), it is supposed that r\ is not constant on [σ1 , σ] and [σ, σ2]. Under some mild restrictions on Ƭ1,- and σ1, (ι = 1,2), it is proved that all solutions of (E) are oscillatory if and only if the characteristic equation
σ1 < σ 2 < ∞ and μ and η are increasing real-valued functions on [Ƭ1, Ƭ2] and [σ1, σ2] respectively. The function μ is assumed to be not constant on [Ƭ1, Ƭ2] and [Ƭ1, Ƭ2] for every Ƭ ∈ (Ƭ1, Ƭ2) similarly, for each σ ∈ (σ1, σ2), it is supposed that r\ is not constant on [σ1 , σ] and [σ, σ2]. Under some mild restrictions on Ƭ1,- and σ1, (ι = 1,2), it is proved that all solutions of (E) are oscillatory if and only if the characteristic equation 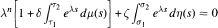 of (E) has no real roots.
of (E) has no real roots.