Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T01:16:22.666Z Has data issue: false hasContentIssue false
  • English
  • Français

Oscillation Criteria for y"" + p(t)f(y,y’) = 0 with f Homogeneous of Degree One

Published online by Cambridge University Press:  20 November 2018

G. B. Gustafson
G. B. Gustafson*
Affiliation:
University of Utah, Salt Lake City, Utah
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 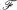be the class of functions f : R2 → R satisfying (1) f is continuous, (2) 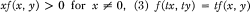for all t, x, y ∈ R, (4) f is locally Lipschitzian. The classical Sturm theorems, the Leighton-Wintner oscillation theorem, and perturbation theorems have been established by Bihari in [1; 2; 3] for the equation , .

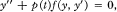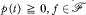This paper investigates the question of strong oscillation of

(1.1)

for p ∈ C[0, ∞ ), f ∈ 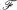. The equation is viewed as “almost linear” because of the homogeneity and sign conditions on f.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 25 , Issue 2 , April 1973 , pp. 323 - 337
Copyright
Copyright © Canadian Mathematical Society 1973

References

1. Bihari, I., Extension of certain theorems of the Sturmian type to nonlinear second order differential equations, Magyar Tud. Akad. Mat. Fiz.Oszt.Közl. 3 (1958), 13–20.Google Scholar
2. Bihari, I., Asymptotic behavior of the solutions of certain second order ordinary differential equations perturbed by a half-linear term, Magyar Tud. Akad. Mat. Fiz.Oszt.Közl. 6 (1961), 291–293, MR 26 (1963), No. 6497.Google Scholar
3. Bihari, I., An oscillation theorem concerning the half-linear differential equation of the second order, Magyar Tud. Akad. Mat. Fiz.Oszt.Kôzl. 8 (1963), 275–280.Google Scholar
4. Hartman, P., Ordinary differential equations (Wiley, New York, 1964).Google Scholar
5. Jackson, L. K., Subfunctions and second-order ordinary differential inequalities, Advances in Math. 2 (1968), 307–363.Google Scholar
6. Leighton, W., The detection of oscillation of solutions of a second order linear differential equation, Duke Math. J. 17 (1950), 57–62.Google Scholar
7. Nehari, Z., Oscillation criteria for second-order linear differential equations, Trans. Amer. Math. Soc. 85 (1957), 428–445.Google Scholar
8. Wong, J. S. W., On second order nonlinear oscillation, Funkcial. Ekvac. 11 (1968), 207–234.Google Scholar