Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T12:10:08.600Z Has data issue: false hasContentIssue false
  • English
  • Français

Oscillation and Nonoscillation Properties of Neutral Differential Equations

Published online by Cambridge University Press:  20 November 2018

L. H. Erbe  and
Qingkai Kong
L. H. Erbe
Affiliation:
Department of Mathematics University of Alberta Edmonton, Alberta T6G 2G1
Qingkai Kong
Affiliation:
Department of Mathematics University of Alberta Edmonton, Alberta T6G 2G1
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We obtain a number of new conditions for oscillation of the first order neutral delay equation with nonconstant coefficients of the form

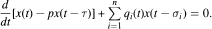
Comparison results are also given as well as conditions for the existence of nonoscillatory solutions.

Keywords

34K15
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 46 , Issue 2 , 01 April 1994 , pp. 284 - 297
Copyright
Copyright © Canadian Mathematical Society 1994

References

1. Anno, O. and Gyori, I., Necessary and sufficient condition for oscillation of a neutral differential system with several delays, J. Differential Equations 81(1989), 98–105.Google Scholar
2. Chuanxi, Q. and Ladas, G., Oscillations of first-order neutral equations with variable coefficients, Monatsh. Math. 109(1990), 103–111.Google Scholar
3. Chen, S. and Huang, Q., On a conjecture of Hunt and Yorke, J. Math. Anal. Appl. 159(1991), 469–484.Google Scholar
4. Chuanxi, Q., Ladas, G., Zhang, B. G. and Zhao, T., Sufficient conditions for oscillation and existence of positive solutions, Applicable Anal. 35(1990), 187–194.Google Scholar
5. Erbe, L. and Kong, Qingkai, Some necessary and sufficient conditions for oscillation of neutral differential equations, preprint.Google Scholar
6. Grammatikopoulos, M. K., Grove, E. A. and Ladas, G., Oscillation of first order neutral delay differential equations, J. Math. Anal. Appl. 120(1986), 510–520.Google Scholar
7. Grammatikopoulos, M. K., Ladas, G. and Meimaridou, A., Oscillation and asymptotic behavior of higher order neutral equations with variable coefficients, Chinese Ann. Math. 3(1988), 322–337.Google Scholar
8. Grammatikopoulos, M. K., Ladas, G. and Sficas, Y. G., Oscillation and asymptotic behavior of neutral equations with variable coefficients, Rad. Mat. 2(1986), 279–303.Google Scholar
9. Grove, E. A., Kulenovic, M. R. S. and Ladas, G., Sufficient conditions for oscillation and nonoscillation of neutral equations, J. Differential Equations 68(1987), 373–382.Google Scholar
10. Grove, E. A., Kulenovic, M. R. S. and Ladas, G., A Myskis-type comparison result for neutral equations, Math. Nachr. 146(1990), 195–206.Google Scholar
11. Huang, Q. and Chen, S., Oscillation of neutral differential equations with periodic coefficients, Proc. Amer. Math. Soc. 110(1990), 997–1001.Google Scholar
12. Hunt, B. R. and Yorke, J. A., When all solutions ofx’ = — £ qix(t— r,-(r)) oscillate, J. Differential Equations 53(1984), 139–145.Google Scholar
13. Ladas, G. and Sficas, Y. G., Oscillations of neutral delay differential equations, Canad. Math. Bull. 29(1986), 438–445.Google Scholar
14 Ladas, G. and Sficas, Y. G., Oscillation of higher-order neutral equations,]. Austral. Math. Soc. Ser. (B) 27(1986), 502–511.Google Scholar
15. Ladas, G., Philos, Ch. G. and Sficas, Y. G., Oscillation in neutral equations with periodic coefficients, Proc. Amer. Math. Soc. 113(1991), 123–134.Google Scholar