Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T04:47:18.019Z Has data issue: false hasContentIssue false
  • English
  • Français

Orthogonal Bundles and Skew-Hamiltonian Matrices

Published online by Cambridge University Press:  20 November 2018

Roland Abuaf  and
Ada Boralevi
Roland Abuaf
Affiliation:
Department of Mathematics, Imperial College London, 180 Queen’s Gate, London SW7 2AZ, UK. e-mail: [email protected]
Ada Boralevi
Affiliation:
Scuola Internazionale Superiore di Studi Avanzati, via Bonomea 265, 34136 Trieste, Italy. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Using properties of skew-Hamiltonian matrices and classic connectedness results, we prove that the moduli space 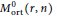$M_{\text{ort}}^{0}\left( r,\,n \right)$ of stable rank $r$ orthogonal vector bundles on 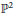${{\mathbb{P}}^{2}}$, with Chern classes 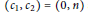$\left( {{c}_{1}},\,{{c}_{2}} \right)\,=\,\left( 0,\,n \right)$ and trivial splitting on the general line, is smooth irreducible of dimension 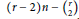$\left( r-2 \right)n\,-\,\left( _{2}^{r} \right)$ for 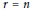$r\,=\,n$ and 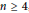$n\,\ge \,4$, and 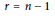$r\,=\,n-1$ and 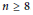$n\,\ge \,8$. We speculate that the result holds in greater generality.

Keywords

14J6015B99orthogonal vector bundlesmoduli spacesskew-Hamiltonian matrices
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 67 , Issue 5 , 01 October 2015 , pp. 961 - 989
Copyright
Copyright © Canadian Mathematical Society 2015

References

[Bar77] Barth, W., Moduli of vector bundles on the projective plane. Invent. Math. 42(1977), 63–91.http://dx.doi.org/10.1007/BF01389784 Google Scholar
[BasOO] Basili, R., On the irreducibility of varieties of commuting matrices. J. Pure Appl. Algebra 149(2000), 107–120. http://dx.doi.org/10.1016/S0022-4049(99)00027-4 Google Scholar
[BeaO6] Beauville, A., Orthogonal bundles on curves and theta functions. Ann. Inst. Fourier (Grenoble) 56(2006), 1405–1418. http://dx.doi.org/10.5802/aif.2216 Google Scholar
[BPV90] Brennan, J. P., Pinto, M. V., and Vasconcelos, W. V., The Jacobian module of a Lie algebra. Trans. Amer. Math. Soc. 321(1990), 183–196. http://dx.doi.org/10.1090/S0002-9947-1990-0958883-0 Google Scholar
[Gro68] Grothendieck, A., Cohomologie locale des faisceaux cohérents et théorèmes de Lefschetz locaux et globaux (SGA 2). Adv. Stud. Pure Math. 2, North–Holland Publishing Co., Amsterdam, 1968.Google Scholar
[GS] Grayson, D. R. and Stillman, M. E., Macaulayl, a software system for research in algebraic geometry. Available at http://www.math.uiuc.edu/Macaulay2/. Google Scholar
[GS05] Gómez, Tomás and, Moduli space of principal sheaves over projective varieties. Ann. of Math. (2) 161(2005), 1037–1092. http://dx.doi.Org/10.4007/annals.2005.161.1037 Google Scholar
[HJM12] Henni, A., Jardim, M., and Martins, R., ADHM construction of perverse instanton sheaves. arxiv:1201.5657, 2012.Google Scholar
[Hul80] Hulek, K., On the classification of stable rank-r vector bundles over the projective plane. In: Vector bundles and differential equations (Proc. Conf, Nice, 1979), Progr. Math. 7(1980), Birkhâuser Boston, Mass., 1980, 113–144.Google Scholar
[Hul81] Hulek, K., On the deformation of orthogonal bundles over the projective line. J. Reine Angew. Math. 329(1981), 52–57.Google Scholar
[JMW14] Jardim, M., Marchesi, S., and Wissdorff, A., Moduli of autodual instanton sheaves. arxiv:1401.6635, 2014.Google Scholar
[Kem76] Kempf, G. R., On the collapsing of homogeneous bundles. Invent. Math. 37(1976), 229–239.http://dx.doi.org/10.1007/BF01390321 Google Scholar
[LazO4] Lazarsfeld, R., Positivity in algebraic geometry. I. Ergeb. Math. Grenzgeb. (3) 48, Springer-Verlag, Berlin, 2004.Google Scholar
[Mum71] Mumford, D., Theta characteristics of an algebraic curve. Ann. Sci. École Norm. Sup. (4) 4(1971), 181–192.Google Scholar
[Nofl3] Noferini, V., When is a Hamiltonian matrix the commutator of two skew-Hamiltonian matrices? Linear Multilinear Algebra, to appear.Google Scholar
[OSM94] Ottaviani, G., Szurek, M., and Manolache, N., On moduli of stable 2-bundles with small Chern classes on Q3. With an appendix by N. Manolache. Annali di Matem. 167(1994), 191–241. http://dx.doi.org/10.1007/BF01760334 Google Scholar
[Ott07] Ottaviani, G., Symplectic bundles on the plane, secant varieties and Lüroth quartics revisited. In: Vector bundles and low codimensional subvarieties: state of the art and recent developments, Quad. Mat. 21(2007), 315–352.Google Scholar
[Ram75] Ramanathan, A., Stable principal bundles on a compact Riemann surface. Math. Ann. 213(1975), 129–152. http://dx.doi.org/10.1007/BF01343949 Google Scholar
[Ram83] Ramanathan, A., Deformations of principal bundles on the projective line. Invent. Math. 71(1983),165–191. http://dx.doi.org/10.1007/BF01393340 Google Scholar
[SerO8] Serman, O., Moduli spaces of orthogonal and symplectic bundles over an algebraic curve. Compos. Math. 144(2008), 721–733.Google Scholar
[WatO5] Waterhouse, W., The structure of alternating–Hamiltonian matrices. Linear Algebra Appl. 396(2005), 385–390. http://dx.doi.Org/10.1016/j.laa.2004.10.003 Google Scholar