Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T00:47:45.268Z Has data issue: false hasContentIssue false
  • English
  • Français

Ordinary Singularities with Decreasing Hilbert Function

Published online by Cambridge University Press:  20 November 2018

Leslie G. Roberts
Leslie G. Roberts*
Affiliation:
Queen's University, Kingston, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A be the co-ordinate ring of a reduced curve over a field k. This means that A is an algebra of finite type over k, A has no nilpotent elements, and that if P is a minimal prime ideal of A, then A/P is an integral domain of Krull dimension one. Let M be a maximal ideal of A. Then G(A) (the graded ring of A relative to M) is defined to be 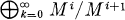. We get the same graded ring if we first localize at M, and then form the graded ring of AM relative to the maximal ideal MAM. That is

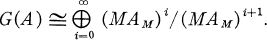
Let Ā be the integral closure of A. If P1, P2, …, Ps are the minimal primes of A then

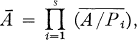
where A/Pi is a domain and 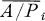is the integral closure of A/Pi in its quotient field.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 34 , Issue 1 , 01 February 1982 , pp. 169 - 180
Copyright
Copyright © Canadian Mathematical Society 1982

References

1. Geramita, A. V. and Orecchia, F., On the Cohen-Macaulay type of s-lines in An+1, J. of Algebra 70 (1981), 116–140.Google Scholar
2. Orecchia, F., Ordinary singularities of algebraic curves, to appear in Canadian Mathematical Bulletin.Google Scholar
3. Orecchia, F., Points in generic position and conductor of curves with ordinary singularities, Preprint.Google Scholar
4. Sally, J., Number of generators of ideals in local rings, Lect. Notes in Pure and Applied Math. 35 (Marcel Dekker, New York, 1978).Google Scholar