Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T01:05:03.375Z Has data issue: false hasContentIssue false
  • English
  • Français

Operator Amenability of the Fourier Algebra in the cb-Multiplier Norm

Published online by Cambridge University Press:  20 November 2018

Brian E. Forrest ,
Volker Runde  and
Nico Spronk
Brian E. Forrest
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, ON, N2L 3G1 email: [email protected], [email protected]
Volker Runde
Affiliation:
Department of Mathematical and Statistical Sciences, University of Alberta, Edmonton, AB, T6G 2G1 email: [email protected]
Nico Spronk
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, ON, N2L 3G1 email: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 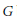$G$ be a locally compact group, and let 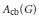${{A}_{\text{cb}}}(G)$ denote the closure of 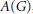$A(G)$, the Fourier algebra of 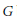$G$, in the space of completely bounded multipliers of 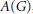$A(G)$. If 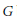$G$ is a weakly amenable, discrete group such that 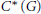${{C}^{*}}(G)$ is residually finite-dimensional, we show that 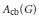${{A}_{\text{cb}}}(G)$ is operator amenable. In particular, 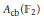${{A}_{\text{cb}}}({{\mathbb{F}}_{2}})$ is operator amenable even though 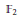${{\mathbb{F}}_{2}}$, the free group in two generators, is not an amenable group. Moreover, we show that if 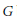$G$ is a discrete group such that 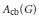${{A}_{\text{cb}}}(G)$ is operator amenable, a closed ideal of 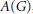$A(G)$ is weakly completely complemented in 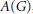$A(G)$ if and only if it has an approximate identity bounded in the 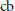$\text{cb}$-multiplier norm.

Keywords

43A2243A3046H2546J1046J4046L0747L25cb-multiplier normFourier algebraoperator amenabilityweak amenability
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 5 , 01 October 2007 , pp. 966 - 980
Copyright
Copyright © Canadian Mathematical Society 2007

References

[A] Aristov, O. Yu., Biprojective algebras and operator spaces. J. Math. Sci. (New York) 111(2002), no. 2, 3339–3386.Google Scholar
[ARS] Aristov, O. Yu., Runde, V., and Spronk, N., Operator biflatness of the Fourier algebra and approximate indicators for subgroups. J. Funct. Anal. 209(2004), no. 2, 367–387.Google Scholar
[BCD] Bade, W. G., Curtis, P. C. Jr., and Dales, H. G., Amenability and weak amenability for Beurling and Lipschitz algebras. Proc. London Math. Soc. 55(1987), no. 2, 359–377.Google Scholar
[BL] Blecher, D. and Le Merdy, C., Operator Algebras and Their Modules—An Operator Space Approach. London Mathematical Society Monographs 30, Clarendon Press, 2004.Google Scholar
[CH] Cowling, M. and Haagerup, U., Completely bounded multipliers of the Fourier algebra of a simple Lie group of real rank one. Invent. Math. 96(1989), no. 3, 507–549.Google Scholar
[Da] Dales, H. G., Banach Algebras and Automatic Continuity. London Mathematical Society Monographs 24, Clarendon Press, New York, 2000.Google Scholar
[DGH] Dales, H. G., Ghahramani, F., and Helemskiiĭ, A. Ya., The amenability of measure algebras. J. London Math. Soc. 66(2002), no. 1, 213–226.Google Scholar
[Dav] Davidson, K. R., C*-Algebras by Example. Fields Institute Monographs 6, American Mathematical Society, Providence, RI, 1996.Google Scholar
[dCH] de Cannière, J. and Haagerup, U.,Multipliers of the Fourier algebras of some simple Lie groups and their discrete subgroups. Amer. J. Math. 107(1985), no. 2, 455–500.Google Scholar
[D1] Dorofaeff, B., The Fourier algebra of SL(2, R) ⋊ R n, n ≥ 2, has no multiplier bounded approximate unit. Math. Ann. 297(1993), no. 4, 707–724.Google Scholar
[D2] Dorofaeff, B., Weak amenability and semidirect products in simple Lie groups. Math. Ann. 306(1996), no. 4, 737–742.Google Scholar
[ER] Effros, E. G. and Ruan, Z.-J., Operator Spaces. London Mathematical Society Monographs 23, Clarendon Press, New York, 2000.Google Scholar
[E] Eymard, P., L’algèbre de Fourier d’un groupe localement compact. Bull. Soc. Math. France 92(1964), 181–236.Google Scholar
[F1] Forrest, B. E., Some Banach algebras without discontinuous derivations. Proc. Amer. Math. Soc. 114(1992), no. 4, 965–970.Google Scholar
[F2] Forrest, B. E., Completely bounded multipliers and ideals in A(G) vanishing on closed subgroups. In: Banach Algebras and Their Applications. Contemp. Math. 363, American Mathematical Society, Providence, RI, 2004, pp. 89–94.Google Scholar
[FKLS] Forrest, B. E., Kaniuth, E., Lau, A. T.-M., and Spronk, N., Ideals with bounded approximate identities in Fourier algebras. J. Funct. Anal. 203(2003), no. 1, 286–304.Google Scholar
[FR] Forrest, B. E. and Runde, V., Amenability and weak amenability of the Fourier algebra. Math. Z. 250(2005), no. 4, 731–744.Google Scholar
[FW] Forrest, B. E. and Wood, P. J., Cohomology and the operator space structure of the Fourier algebra and its second dual. Indiana Univ. Math. J. 50(2001), no. 3, 1217–1240.Google Scholar
[HK] Haagerup, U. and Kraus, J., Approximation properties for group C*-algebras and group von Neumann algebras . Trans. Amer. Math. Soc. 344(1994), no. 2, 667–699.Google Scholar
[H1] Helemskiĭ, A. Ya., The Homology of Banach and Topological Algebras. (translated from the Russian), Mathematics and its Applications (Soviet Series) 41, Kluwer, Dordrecht, 1989.Google Scholar
[H2] Helemskiĭ, A. Ya., Some aspects of topological homology since 1995: a survey. In: Banach Algebras and Their Applications. Contemp. Math. 363, American Mathematical Society, Providence, RI, 2004, pp. 145–179.Google Scholar
[IS] Ilie, M. and Spronk, N., Completely bounded homomorphisms of the Fourier algebras. J. Funct. Anal. 225(2005), no. 2, 480–499.Google Scholar
[J1] Johnson, B. E., Cohomology in Banach algebras. Memoirs of the American Mathematical Society 127,. American Mathematical Society, Providence, RI, 1972.Google Scholar
[J2] Johnson, B. E., Weak amenability of group algebras. Bull. London Math. Soc. 23(1991), no. 3, 281–284.Google Scholar
[J3] Johnson, B. E., Non-amenability of the Fourier algebra of a compact group. J. London Math. Soc. 50(1994), no. 2, 361–374.Google Scholar
[KL] Kaniuth, E. and Lau, A. T.-M., Spectral synthesis A(G) and for subspaces of VN(G). Proc. Amer. Math. Soc. 129(2001), no. 11, 3253–3263.Google Scholar
[LNR] Lambert, A., Neufang, M., and Runde, V., Operator space structure and amenability for Figà-Talamanca–Herz algebras. J. Funct. Anal. 211(2004), no. 1, 245–269.Google Scholar
[Le] Leptin, H., Sur l’algèbre de Fourier d’un groupe localement compact. C. R. Acad. Sci. Paris Sér. A-B 266(1968), A1180–A1182.Google Scholar
[LRRW] Loy, R. J., Read, C. J., Runde, V., and Willis, G. A., Amenable and weakly amenable Banach algebras with compact multiplication. J. Funct. Anal. 171(2000), no. 1, 78–114.Google Scholar
[R] Ruan, Z.-J., The operator amenability of A(G). Amer. J. Math. 117(1995), no. 6, 1449–1474.Google Scholar
[Ru1] Runde, V., Lectures on Amenability. Lecture Notes in Mathematics 1774, Springer-Verlag, Berlin, 2002.Google Scholar
[Ru2] Runde, V., Amenability for dual Banach algebras. Studia Math. 148(2001), no. 1, 47–66.Google Scholar
[Ru3] Runde, V., Connes-amenability and normal, virtual diagonals for measure algebras. I. J. London Math. Soc. 67(2003), no. 3, 643–656.Google Scholar
[Ru4] Runde, V., Dual Banach algebras: Connes-amenability, normal, virtual diagonals, and injectivity of the predual bimodule. Math. Scand. 95(2004), no. 1, 124–144.Google Scholar
[Ru5] Runde, V., Applications of operator spaces to abstract harmonic analysis. Expo. Math. 22(2004), no. 4, 317–363.Google Scholar
[Ru6] Runde, V., The amenability constant of the Fourier algebra. Proc. Amer. Math. Soc. 134(2006), no. 5, 1473–1481.(electronic).Google Scholar
[RS] Runde, V. and Spronk, N., Operator amenability of Fourier-Stieltjes algebras. Math. Proc. Cambridge Phil. Soc. 136(2004), no. 3, 675–686.Google Scholar
[S1] Spronk, N., Operator weak amenability of the Fourier algebra. Proc. Amer. Math. Soc. 130(2002), no. 12, 3609–3617.Google Scholar
[S2] Spronk, N., Measurable Schur multipliers and completely bounded multipliers of the Fourier algebras. Proc. London Math. Soc. 89(2004), no. 1, 161–192.Google Scholar
[W1] Wood, P. J., Complemented ideals in the Fourier algebra of a locally compact group. Proc. Amer. Math. Soc. 128(2000), no. 2, 445–451.Google Scholar
[W2] Wood, P. J., The operator biprojectivity of the Fourier algebra. Canad. J. Math. 54(2002), no. 5, 1100–1120.Google Scholar