Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-19T03:18:26.556Z Has data issue: false hasContentIssue false
  • English
  • Français

One-Parameter Continuous Fields of Kirchberg Algebras. II

Published online by Cambridge University Press:  20 November 2018

Marius Dadarlat ,
George A. Elliott  and
Zhuang Niu
Marius Dadarlat
Affiliation:
Department of Mathematics, Purdue University, West Lafayette, IN 47907, U.S.A. email: [email protected]
George A. Elliott
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ON M5S 2E4 email: [email protected]
Zhuang Niu
Affiliation:
Department of Mathematics, University of Oregon, Eugene, OR 97403, U.S.A. and Department of Mathematics, Memorial University of Newfoundland, St. John’s, NL A1C 5S7 email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Parallel to the first two authors’ earlier classification of separable, unital, one-parameter, continuous fields of Kirchberg algebras with torsion free 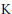$\text{K}$-groups supported in one dimension, one-parameter, separable, unital, continuous fields of 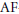$\text{AF}$-algebras are classified by their ordered 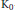${{\text{K}}_{0}}$-sheaves. Effros-Handelman-Shen type theorems are proved for separable unital one-parameter continuous fields of 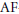$\text{AF}$-algebras and Kirchberg algebras.

Keywords

46L35continuous fields of C*-algebrasK0-presheavesEffros-Handelman-Shen type theorem
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 3 , 01 June 2011 , pp. 500 - 532
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Blanchard, E. and Kirchberg, E., Global Glimm halving for C¤-bundles. J. Operator Theory 52(2004), no. 2, 385–420.Google Scholar
[2] Dadarlat, M. and Elliott, G. A., One-parameter continuous fields of Kirchberg algebras. Comm. Math. Phys. 274(2007), no. 3, 795–819. doi:10.1007/s00220-007-0298-z Google Scholar
[3] Dixmier, J., C¤-algebras. North-Holland Mathematical Library, 15, North-Holland Publishing Co., Amsterdam-New York-Oxford, 1977.Google Scholar
[4] Elliott, G. A. and Rørdam, M., Classification of certain infinite simple C¤-algebras. II. Comment. Math. Helv. 70(1995), no. 4, 615–638. doi:10.1007/BF02566025 Google Scholar
[5] Loring, T. A., Lifting solutions to perturbing problems in C¤-algebras. Fields Institute Monographs, 8, American Mathematical Society, Providence, RI, 1997.Google Scholar
[6] Nagy, G., Some remarks on lifting invertible elements from quotient C¤-algebras. J. Operator Theory 21(1989), no. 2, 379–386.Google Scholar
[7] Rørdam, M., Larsen, F., and Laustsen, N. J., An introduction to K-Theory for C¤-algebras. London Mathematical Society Student Texts, 49, Cambridge University Press, Cambridge, 2000.Google Scholar
[8] Shen, C.-L., On the classification of the ordered groups associated with the approximately finite-dimensional C¤-algebras. Duke Math. J. 46(1979), no. 3, 613–633. doi:10.1215/S0012-7094-79-04632-5 Google Scholar
[9] Su, H., On the classification of C¤-algebras of real rank zero: inductive limits of matrix algebras over non-Hausdorff graphs. Mem. Amer. Math. Soc. 114(1995), no. 547.Google Scholar
[10] Tomiyama, J. and Takesaki, M., Applications of fibre bundles to the certain class of C¤-algebras. Tôhoku Math. J. 13(1961), 498–522. doi:10.2748/tmj/1178244253 Google Scholar