Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T00:32:48.274Z Has data issue: false hasContentIssue false
  • English
  • Français

On Unitary Polarities of Finite Projective Planes

Published online by Cambridge University Press:  20 November 2018

William M. Kantor
William M. Kantor*
Affiliation:
University of Illinois, Chicago, Illinois
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

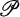A unitary polarity of a finite projective plane of order q2 is a polarity θ having q3 + 1 absolute points and such that each nonabsolute line contains precisely q + 1 absolute points. Let G(θ) be the group of collineations of 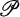centralizing θ. In [15] and [16], A. Hoffer considered restrictions on G(θ) which force 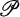to be desarguesian. The present paper is a continuation of Hoffer's work. The following are our main results.

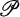THEOREM I. Let θ be a unitary polarity of a finite projective planeof order q2. Suppose that Γ is a subgroup of G(θ) transitive on the pairs x, X, with x an absolute point and X a nonabsolute line containing x. Then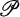is desarguesian and Γ contains PSU(3, q).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 23 , Issue 6 , December 1971 , pp. 1060 - 1077
Copyright
Copyright © Canadian Mathematical Society 1971

References

1. Alperin, J. L., Brauer, R., and Gorenstein, D., Finite groups with quasi-dihedral and wreathed Sylow 2-subgroups, Trans. Amer. Math. Soc. 151 (1970), 1–261.Google Scholar
2. Alperin, J. L., Brauer, R., and Gorenstein, D., Finite simple groups of 2-rank two (to appear).Google Scholar
3. Alperin, J. L. and Gorenstein, D., The multiplicators of certain simple groups, Proc. Amer. Math. Soc. 17 (1966), 515–519.Google Scholar
4. Bender, H., Endliche zweifach transitive permutations Gruppen, deren Involutionen keine Fixpunkte haben, Math. Z. 104 (1968), 175–204.Google Scholar
5. Bender, H., Transitive Gruppen gerader Ordnung, in denen jede Involution genau einen Punkt festlasst, J. Algebra 17 (1971), 527–554.Google Scholar
6. Bloom, D. M., The subgroups o/PSL(3, q) for q odd, Trans. Amer. Math. Soc. 127 (1967), 150–178.Google Scholar
7. Dembowski, P., Finite Geometries (Springer, Berlin, 1968).Google Scholar
8. Dickson, L. E., Linear groups (Dover, New York, 1955).Google Scholar
9. Feit, W. and Thompson, J. G., Solvability of groups of odd order, Pacific J. Math. 13 (1963), 771–1029.Google Scholar
10. Gorenstein, D., Finite groups (Harper and Row, New York, 1968).Google Scholar
11. Gorenstein, D. and Walter, J. H., The characterization of finite groups with dihedral Sylow 2-subgroups. I, II, III, J. Algebra 2 (1965), 85-151, 218–270, 354-393.Google Scholar
12. Hall, M., Jr., The theory of groups (MacMillan, New York, 1959).Google Scholar
13. Hering, C., Zweifach transitive Per mutations gruppen, in denen zwei die maximale Anzahl von Fixpunkte von Involutionen ist, Math. Z. 104 (1968), 150–174.Google Scholar
14. Hering, C., Kantor, W. M., and Seitz, G. M., Finite groups with a split BN-pair of rank 2 (to appear).Google Scholar
15. Hoffer, A., Polarities on theLenz-Barlotti classification, Ph.D. thesis, University of Michigan, Ann Arbor, Michigan, 1969.Google Scholar
16. Hoffer, A., On unitary collineation groups (to appear).Google Scholar
17. Kantor, W. M., 2-Transitive groups in which the stabilizer of two points fixes additional points (to appear).Google Scholar
18. Kantor, W. M. and Seitz, G. M., Some results on2-transitive groups, Invent. Math. 13 (1971), 125–142.Google Scholar
19. Liineburg, H., Zur Frage der Existenz von endlichen projektiven Ebenen vont Lenz-Barlotti- Typ III-2, J. Reine Angew. Math. 220 (1965), 63–67.Google Scholar
20. Lyons, R., On some finite simple groups of small 2-rank, Ph.D. thesis, University of Chicago, Chicago, Illinois, 1970.Google Scholar
21. Mitchell, H. H., Determination of the ordinary and modular ternary linear groups, Trans. Amer. Math. Soc. 12 (1911), 207–242.Google Scholar
22. O'Nan, M., A characterization of the 3-dimensional projective unitary group over a finite field, Ph.D. thesis, Princeton University, Princeton, N. J., 1969.Google Scholar
23. Ostrom, T. G., Double transitivity in finite projective planes Can. J. Math. 8 (1956). 563–567.Google Scholar
24. Ostrom, T. G., Dual transitivity in finite projective planes, Proc. Amer. Math. Soc. 9 (1958), 55–56.Google Scholar
25. Schur, I., Untersuchungen iiber die Darstellungen der endlichen Gruppen durch gebrochene lineare Substitutionen, J. Reine Angew. Math. 182 (1907), 85–137.Google Scholar
26. Seib, M., Unitàre Polaritàten endlicher projektiver Ebenen, Arch. Math. 21 (1970), 103–112.Google Scholar
27. Shult, E., On the fusion of an involution in its centralizer (to appear).Google Scholar
28. Shult, E., On a class of doubly transitive groups (to appear).Google Scholar
29. Suzuki, M., On a class of doubly transitive groups, Ann. of Math. 75 (1962), 105–145.Google Scholar