No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
Similarity invariants of certain families of Volterra operators acting in Lp[0, 1] were first determined by Kalisch in [4] and [5]. Subsequently, Kantorovitz made an extensive study of perturbations of the form Tα = M + αN, where M is the operation of multiplication by x, and N is the Volterra operator
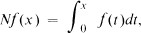
both acting in Lp[0, 1], and determined that Re α is a similarity invariant for the class of Tα's (cf. [7], and earlier work cited there). This result was eventually generalized to unbounded M (cf. [6]), and one direction was proved in [2] for both M and N unbounded: if Re α = Re β, then Tα is similar to Tβ. Properties of the Riemann-Liouville semigroup of fractional integration play a key role, for in all cases the ensuing similarity turns out to be implemented by N(i(lm(α — β))), where {N(iγ)} is the boundary group of the semigroup of fractional integration.