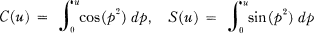Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kreyszig, Erwin
1957.
On the Complementary Functions of the Fresnel
Integrals.
Canadian Journal of Mathematics,
Vol. 9,
Issue. ,
p.
500.
Barakat, Richard
1961.
Evaluation of the incomplete gamma function of imaginary argument by Chebyshev polynomials.
Mathematics of Computation,
Vol. 15,
Issue. 73,
p.
7.
1973.
Table Errata.
Mathematics of Computation,
Vol. 27,
Issue. 121,
p.
219.
Fettis, Henry E.
and
Caslin, James C.
1973.
Erratum: Handbook of mathematical functions with formulas, graphs, and mathematical tables (Nat. Bur. Standards, Washington, D.C., 1964) edited by Milton Abramowitz and Irene A. Stegun.
Mathematics of Computation,
Vol. 27,
Issue. 121,
p.
219.
1975.
Mathematical Functions and their Approximations.
p.
517.
Riccardi, Giorgio
2011.
Remarks on the solution of extended Stokes' problems.
International Journal of Non-Linear Mechanics,
Vol. 46,
Issue. 7,
p.
958.