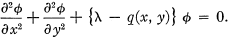Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Sears, D. B.
1950.
Note on the Uniqueness of the Green'S Functions Associated With Certain Differential Equations.
Canadian Journal of Mathematics,
Vol. 2,
Issue. ,
p.
314.
Wienholtz, Ernst
1959.
Bemerkungen �ber elliptische Differentialoperatoren.
Archiv der Mathematik,
Vol. 10,
Issue. 1,
p.
126.
Patula, W. T.
and
Wong, J. S. W.
1972.
AnL p -analogue of the Weyl alternative.
Mathematische Annalen,
Vol. 197,
Issue. 1,
p.
9.
Wong, James S. W.
and
Zettl, Anton
1973.
On the limit point classification of second order differential equations.
Mathematische Zeitschrift,
Vol. 132,
Issue. 4,
p.
297.
Atkinson, Frederick V.
1973.
Nonlinear extensions of limit-point criteria.
Mathematische Zeitschrift,
Vol. 130,
Issue. 4,
p.
297.
Wong, James S. W.
1974.
Ordinary and Partial Differential Equations.
Vol. 415,
Issue. ,
p.
282.
Eastham, M. S. P.
1974.
Ordinary and Partial Differential Equations.
Vol. 415,
Issue. ,
p.
109.
Gimadislamov, M. G.
1976.
Conditions for the self-adjointness of a quasi-elliptic operator.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 20,
Issue. 5,
p.
957.
Eastham, M. S. P.
Evans, W. D.
and
McLeod, J. B.
1976.
The essential self-adjointness of Schrödinger-type operators.
Archive for Rational Mechanics and Analysis,
Vol. 60,
Issue. 2,
p.
185.
Atkinson, F. V.
1976.
ASYMPTOTIC INTEGRATION AND THE L2-CLASSIFICATION OF SQUARES OF SECOND-ORDER DIFFERENTIAL OPERATORS.
Quaestiones Mathematicae,
Vol. 1,
Issue. 2,
p.
155.
Otelbaev, M.
1977.
Conditions foe self-adjointness of the Schr�dinger operator with operator potential.
Ukrainian Mathematical Journal,
Vol. 28,
Issue. 6,
p.
586.
Knowles, Ian
1978.
On essential self-adjointness for Schrödinger operators with wildly oscillating potentials.
Journal of Mathematical Analysis and Applications,
Vol. 66,
Issue. 3,
p.
574.
Graef, John R.
1979.
Limit circle type criteria for nonlinear differential equations.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 55,
Issue. 2,
Graef, John R
1980.
Limit circle criteria and related properties for nonlinear equations.
Journal of Differential Equations,
Vol. 35,
Issue. 3,
p.
319.
Kurss, H.
and
Meyer, G.
1981.
Limit-point (LP) criteria for real symmetric differential expressions of order 2n.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 88,
Issue. 3-4,
p.
203.
Hazewinkel, M.
1993.
Encyclopaedia of Mathematics.
p.
1.
Браверман, Михаил Ш
Braverman, Mikhail Sh
Милатович, О
Milatovic, O
Шубин, Михаил Александрович
and
Shubin, Mikhail Aleksandrovich
2002.
Существенная самосопряженность операторов типа Шрeдингера на многообразиях.
Успехи математических наук,
Vol. 57,
Issue. 4,
p.
3.
Bartu[sbreve]ek, Miroslav
and
Graef, John R.
2004.
Some Limit-point and Limit-circle Results for Second Order Emden–Fowler Equations.
Applicable Analysis,
Vol. 83,
Issue. 5,
p.
461.
Qi, Jiangang
2007.
Limit-point criteria for semi-degenerate singular Hamiltonian differential systems with perturbation terms.
Journal of Mathematical Analysis and Applications,
Vol. 334,
Issue. 2,
p.
983.
Annaby, M. H.
Hassan, H. A.
and
Mansour, Z. S.
2012.
Sampling Theorems Associated with Singular q-Sturm Liouville Problems.
Results in Mathematics,
Vol. 62,
Issue. 1-2,
p.
121.
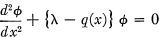
 is of importance in the theory of the expansion of an arbitrary function in terms of the solutions of the differential equation. It is proved that this function is unique if q(x) ≧ — Ax2— B, where A and B are positive constants or zero. A similar theorem is proved for the Green's function G(x, y, ξ, η, λ) associated with the partial differential equation
is of importance in the theory of the expansion of an arbitrary function in terms of the solutions of the differential equation. It is proved that this function is unique if q(x) ≧ — Ax2— B, where A and B are positive constants or zero. A similar theorem is proved for the Green's function G(x, y, ξ, η, λ) associated with the partial differential equation