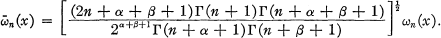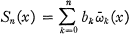Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Saber, Asma Ben
and
Karoui, Abderrazek
2025.
Orthogonal systems based stable estimator for non parametric regression problems.
Communications in Statistics - Theory and Methods,
Vol. 54,
Issue. 5,
p.
1299.


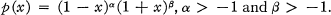
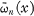 we Have
we Have