Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-29T01:01:23.040Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Structure of the Spreading Models of a Banach Space

Published online by Cambridge University Press:  20 November 2018

G. Androulakis ,
E. Odell ,
Th. Schlumprecht  and
N. Tomczak-Jaegermann
G. Androulakis
Affiliation:
Department of Mathematics, University of South Carolina, Columbia, SC 29208, U.S.A., e-mail: [email protected]
E. Odell
Affiliation:
Department of Mathematics, University of Texas at Austin, Austin, TX 78712, U.S.A., e-mail: [email protected]
Th. Schlumprecht
Affiliation:
Department of Mathematics, Texas A&M University, College Station, TX 77843, U.S.A., e-mail: [email protected]
N. Tomczak-Jaegermann
Affiliation:
Department of Mathematical Sciences, University of Alberta, Edmonton, Alberta, T6G 2G1 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study some questions concerning the structure of the set of spreading models of a separable infinite-dimensional Banach space $X$. In particular we give an example of a reflexive $X$ so that all spreading models of $X$ contain 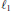${{\ell }_{1}}$ but none of them is isomorphic to 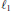${{\ell }_{1}}$. We also prove that for any countable set $C$ of spreading models generated by weakly null sequences there is a spreading model generated by a weakly null sequence which dominates each element of $C$. 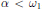In certain cases this ensures that $X$ admits, for each $\alpha \,<\,{{\omega }_{1}}$, a spreading model 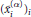${{\left( \tilde{x}_{i}^{\left( \alpha \right)} \right)}_{i}}$ such that if 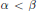$\alpha \,<\,\beta $ then 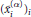${{\left( \tilde{x}_{i}^{\left( \alpha \right)} \right)}_{i}}$ is dominated by (and not equivalent to) 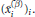${{\left( \tilde{x}_{i}^{\left( \beta \right)} \right)}_{i}}$. Some applications of these ideas are used to give sufficient conditions on a Banach space for the existence of a subspace and an operator defined on the subspace, which is not a compact perturbation of a multiple of the inclusion map.

Keywords

46B03
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 57 , Issue 4 , 01 August 2005 , pp. 673 - 707
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Androulakis, G. and Th. Schlumprecht, Strictly singular non-compact operators exist on the space of Gowers-Maurey. J. London Math. Soc. (2) 64 (2001), 1–20.Google Scholar
[2] Argyrosa, S. A. and Deliyanni, I., Examples of asymptotic ℓ1 Banach spaces. Trans. Amer.Math. Soc. 349(1997), 973–995.Google Scholar
[3] Beauzamy, B. and Lapreste, J.-T.,Modèles étalés des espaces de Banach. Travaux en Cours, Hermann, Paris, 1984.Google Scholar
[4] Brunel, A. and Sucheston, L., On B convex Banach spaces. Math. Systems Theory 7(1974), 294–299.Google Scholar
[5] Brunel, A. and Sucheston, L., On J-convexity and some ergodic super-properties of Banach spaces. Trans. Amer. Math. Soc. 204(1975), 79–90.Google Scholar
[6] Ferenczi, V., Pelczar, A. M., and C. Rosendal, On a question of Haskell P. Rosenthal concerning a characterization of c0 and lp. Bull. LondonMath. Soc. 36(2004), 396–406.Google Scholar
[7] Gasparis, I., A continuum of totally incomparable hereditarily indecomposable Banach spaces. Studia Math. 151(2002), 277–298.Google Scholar
[8] Gasparis, I., Strictly singular non-compact operators on hereditarily indecomposable Banach spaces. Proc. Amer.Math. Soc. 131(2003), 1181–1189.Google Scholar
[9] Gowers, W. T., A remark about the scalar-plus-compact problem. In: Convex geometric analysis (Berkeley, CA, 1996),Math. Sci. Res. Inst. Publ. 34, Cambridge Univ. Press, Cambridge, 1999, pp. 111–115.Google Scholar
[10] Gowers, W. T. and Maurey, B., The unconditional basic sequence problem. J. Amer.Math. Soc. 6(1993), 851–8740.Google Scholar
[11] Halbeisen, L. and Odell, E., On asymptotic models in Banach spaces. Israel J. Math. 139(2004), 253–291.Google Scholar
[12] James, R. C., Bases and reflexivity of Banach spaces. Ann. of Math. (2), 52(1950), 518–527.Google Scholar
[13] Knaust, H., Odell, E., and Th. Schlumprecht, On asymptotic structure, the Szlenk index and UKK properties in Banach spaces. Positivity 3 (1999), 173–199.Google Scholar
[14] Krivine, J. L., Sous-espaces de dimension finie des espaces de Banach réticulés. Ann. of Math. 104 (1976), 1–29.Google Scholar
[15] Lemberg, H., Sur un théorème J.-L. de Krivine sur la fine représentation de lp dans un espace de Banach. C. R. Acad. Sci. Paris Sér. I Math. 292(1981), 669–670.Google Scholar
[16] Lindenstrauss, J. and Tzafriri, L., Classical Banach Spaces. I. Sequence Spaces. Springer-Verlag, Berlin, 1977.Google Scholar
[17] Lindenstrauss, J. and Tzafriri, L., Classical Banach Spaces. II. Function Spaces. Springer-Verlag, Berlin, 1979.Google Scholar
[18] Maurey, B. and Rosenthal, H., Normalized weakly null sequence with no unconditional subsequence. Studia Math. 61(1977), 77–98.Google Scholar
[19] Milman, V. D. and Schechtman, G., Asymptotic theory of finite-dimensional normed spaces. With an appendix by Gromov, M.. Lecture Notes in Mathematics 1200, Springer-Verlag, Berlin, 1986.Google Scholar
[20] Milman, V. D. and Tomczak-Jaegermann, N. Stabilized asymptotic structures and envelops in Banach spaces. In: Geometric Aspects of Functional Analysis (Israel Seminar 1996-2000), Lecture Notes in Math. 1745, Springer, Berlin, 2000, pp. 223–237.Google Scholar
[21] Odell, E., On Schreier unconditional sequences. ContemporaryMath., 144(1993), 197–201.Google Scholar
[22] Odell, E. and Th. Schlumprecht, On the richness of the set of p's in Krivine's theorem. In: Geometric Aspects of Functional Analysis (Israel Seminar 1992–1994), Oper. Theory Adv. Appl. 77, Birkhäuser, Basel, 1995, pp. 177–198.Google Scholar
[23] Odell, E. and Th. Schlumprecht, A problem on spreading models. J. Funct. Anal. 153(1998), 249–261.Google Scholar
[24] Odell, E. and Th. Schlumprecht, A Banach space block finitely universal for monotone bases. Trans. Amer. Math. Soc. 352(2000), 1859–1888.Google Scholar
[25] Ramsey, F. P., On a problem of formal logic. Proc. LondonMath. Soc. (2), 30(1929), 264–286.Google Scholar
[26] Rosenthal, H., A characterization of Banach spaces containing ℓ1. Proc. Nat. Acad. Sci. U.S.A. 71(1974), 2411–2413.Google Scholar
[27] Rosenthal, H., Some remarks concerning unconditional basic sequences. Texas Functional Analysis Seminar 1982–1983, Longhorn Notes, Univ. Texas Press, Austin, TX, 1983, pp. 15–47.Google Scholar
[28] Schlumprecht, Th., An arbitrarily distortable Banach space. Israel J. Math. 76(1991), 81–95.Google Scholar
[29] Schlumprecht, Th., How many operators exist on a Banach space? In: Trends in Banach spaces and operator theory (Memphis, TN, 2001), Contemp.Math 321, Amer.Math. Soc., Providence, RI, 2003, pp. 295–333.Google Scholar