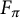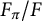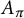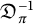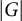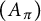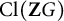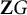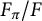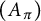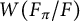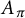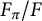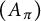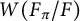1 Introduction
Let F be a number field with absolute Galois group
![]() $\Omega _F$
. Suppose that G is a finite group on which
$\Omega _F$
. Suppose that G is a finite group on which
![]() $\Omega _F$
acts trivially, and let
$\Omega _F$
acts trivially, and let
![]() $\pi : \Omega _F \to G$
be a surjective homomorphism. Let
$\pi : \Omega _F \to G$
be a surjective homomorphism. Let
![]() $F_{\pi }$
be the corresponding G-Galois-algebra extension of F. (We note that since
$F_{\pi }$
be the corresponding G-Galois-algebra extension of F. (We note that since
![]() $\pi $
is surjective,
$\pi $
is surjective,
![]() $F_{\pi }$
is in fact a number field, and not merely a Galois algebra.) Write
$F_{\pi }$
is in fact a number field, and not merely a Galois algebra.) Write
![]() $\mathfrak {D}_\pi $
for the different of
$\mathfrak {D}_\pi $
for the different of
![]() $F_{\pi }/F$
and
$F_{\pi }/F$
and
![]() $O_{\pi }$
for the ring of integers of
$O_{\pi }$
for the ring of integers of
![]() $F_{\pi }$
. If
$F_{\pi }$
. If
![]() $\mathfrak {P}$
is any prime of
$\mathfrak {P}$
is any prime of
![]() $O_{\pi }$
, the power
$O_{\pi }$
, the power
![]() $v_{\mathfrak {P}}(\mathfrak {D}_{\pi })$
of
$v_{\mathfrak {P}}(\mathfrak {D}_{\pi })$
of
![]() $\mathfrak {P}$
occurring in
$\mathfrak {P}$
occurring in
![]() $\mathfrak {D}_\pi $
is given by
$\mathfrak {D}_\pi $
is given by
where
![]() $G^{(i)}_{\mathfrak {P}}$
denotes the ith ramification group at
$G^{(i)}_{\mathfrak {P}}$
denotes the ith ramification group at
![]() $\mathfrak {P}$
(see [Reference Serre23, Chapter IV, Proposition 4]). This implies that if, for example,
$\mathfrak {P}$
(see [Reference Serre23, Chapter IV, Proposition 4]). This implies that if, for example,
![]() $|G|$
is odd, then the inverse different
$|G|$
is odd, then the inverse different
![]() $\mathfrak {D}_{\pi }^{-1}$
has a square root, i.e., there exists a unique fractional ideal
$\mathfrak {D}_{\pi }^{-1}$
has a square root, i.e., there exists a unique fractional ideal
![]() $A_\pi $
of
$A_\pi $
of
![]() $O_{\pi }$
such that
$O_{\pi }$
such that
(Let us remark at once that if
![]() $|G|$
is even, then
$|G|$
is even, then
![]() $\mathfrak {D}_{\pi }^{-1}$
may well—but of course need not—also have a square root.)
$\mathfrak {D}_{\pi }^{-1}$
may well—but of course need not—also have a square root.)
Recall that
![]() $F_{\pi }/F$
is said to be weakly ramified if
$F_{\pi }/F$
is said to be weakly ramified if
![]() $G^{(2)}_{\mathfrak {P}} = 1$
for all prime ideals
$G^{(2)}_{\mathfrak {P}} = 1$
for all prime ideals
![]() $\mathfrak {P}$
of
$\mathfrak {P}$
of
![]() $O_{\pi }$
. Erez has shown that
$O_{\pi }$
. Erez has shown that
![]() $F_{\pi }/F$
is weakly ramified if and only if
$F_{\pi }/F$
is weakly ramified if and only if
![]() $A_\pi $
is a locally free
$A_\pi $
is a locally free
![]() $O_FG$
-module (see [Reference Erez10, Theorem 1]). Hence, if
$O_FG$
-module (see [Reference Erez10, Theorem 1]). Hence, if
![]() $F_{\pi }/F$
is weakly ramified, it follows that
$F_{\pi }/F$
is weakly ramified, it follows that
![]() $A_\pi $
is a locally free
$A_\pi $
is a locally free
![]() ${\mathbf Z} G$
-module, and so defines an element
${\mathbf Z} G$
-module, and so defines an element
![]() $(A_\pi )$
in the locally free class group
$(A_\pi )$
in the locally free class group
![]() $\operatorname {\mathrm {Cl}}(\mathbf {Z} G)$
of
$\operatorname {\mathrm {Cl}}(\mathbf {Z} G)$
of
![]() $\mathbf {Z} G$
. The following result is due to Erez (see [Reference Erez10, Theorem 3]).
$\mathbf {Z} G$
. The following result is due to Erez (see [Reference Erez10, Theorem 3]).
Theorem 1.1 Suppose that
![]() $F_{\pi }/F$
is tamely ramified and that
$F_{\pi }/F$
is tamely ramified and that
![]() $|G|$
is odd. Then
$|G|$
is odd. Then
![]() $A_\pi $
is a free
$A_\pi $
is a free
![]() $\mathbf {Z} G$
-module.
$\mathbf {Z} G$
-module.
Based on this and other results, Vinatier has made the following conjecture (cf. [Reference Vinatier30, Conjecture] and [Reference Caputo and Vinatier4, Section 1.2]).
Conjecture 1.2 Suppose that
![]() $F_{\pi }/F$
is weakly ramified and that
$F_{\pi }/F$
is weakly ramified and that
![]() $|G|$
is odd. Then
$|G|$
is odd. Then
![]() $A_\pi $
is a free
$A_\pi $
is a free
![]() $\mathbf {Z} G$
-module.
$\mathbf {Z} G$
-module.
The first detailed study of the Galois structure of
![]() $A_\pi $
when
$A_\pi $
when
![]() $|G|$
is even is due to the third author and Vinatier [Reference Caputo and Vinatier4]. By studying the Galois structure of certain torsion modules first considered by Chase [Reference Chase6], they proved the following result, and thereby were able to exhibit the first examples for which
$|G|$
is even is due to the third author and Vinatier [Reference Caputo and Vinatier4]. By studying the Galois structure of certain torsion modules first considered by Chase [Reference Chase6], they proved the following result, and thereby were able to exhibit the first examples for which
![]() $(A_\pi ) \neq 0$
in
$(A_\pi ) \neq 0$
in
![]() $\operatorname {\mathrm {Cl}}(\mathbf {Z} G)$
(see [Reference Caputo and Vinatier4, Theorem 2]).
$\operatorname {\mathrm {Cl}}(\mathbf {Z} G)$
(see [Reference Caputo and Vinatier4, Theorem 2]).
Theorem 1.3 Suppose that
![]() $F_{\pi }/F$
is tame and locally abelian (i.e., the decomposition group at every ramified prime of
$F_{\pi }/F$
is tame and locally abelian (i.e., the decomposition group at every ramified prime of
![]() $F_{\pi }/F$
is abelian). Assume also that
$F_{\pi }/F$
is abelian). Assume also that
![]() $A_\pi $
exists. Then
$A_\pi $
exists. Then
![]() $(A_\pi ) = (O_{\pi })$
in
$(A_\pi ) = (O_{\pi })$
in
![]() $\operatorname {\mathrm {Cl}}(\mathbf {Z} G)$
.
$\operatorname {\mathrm {Cl}}(\mathbf {Z} G)$
.
A well-known theorem of M. Taylor [Reference Taylor26] asserts that, if
![]() $F_\pi /F$
is tame, then
$F_\pi /F$
is tame, then
where
![]() $W(F_\pi /F)$
denotes the Cassou–Noguès–Fröhlich root number class, which is defined in terms of Artin root numbers attached to nontrivial irreducible symplectic characters of G. (In particular, if
$W(F_\pi /F)$
denotes the Cassou–Noguès–Fröhlich root number class, which is defined in terms of Artin root numbers attached to nontrivial irreducible symplectic characters of G. (In particular, if
![]() $|G|$
is odd, and so has no nontrivial irreducible symplectic characters, then
$|G|$
is odd, and so has no nontrivial irreducible symplectic characters, then
![]() $W(F_{\pi }/F) = 0$
.)
$W(F_{\pi }/F) = 0$
.)
We therefore see that Theorem 1.3 may be viewed as saying that if
![]() $F_{\pi }/F$
is tame and locally abelian, and if
$F_{\pi }/F$
is tame and locally abelian, and if
![]() $A_\pi $
exists, then we have
$A_\pi $
exists, then we have
In light of the results described above, as well as those contained in [Reference Chinburg7], Erez has made the following (unpublished) conjecture.
Conjecture 1.4 Suppose that
![]() $F_{\pi }/F$
is weakly ramified and that
$F_{\pi }/F$
is weakly ramified and that
![]() $A_\pi $
exists. Then
$A_\pi $
exists. Then
Conjecture 1.4 includes Vinatier’s Conjecture 1.2 as a special case, and was the motivation for the work described in [Reference Caputo and Vinatier4]. It also explains almost all previously obtained results on the
![]() $\mathbf {Z} G$
-structure of
$\mathbf {Z} G$
-structure of
![]() $A_\pi $
. In a different direction, the conjecture is related to the recent work of Bley, Hahn, and the second author [Reference Bley, Burns and Hahn3] concerning metric structures arising from
$A_\pi $
. In a different direction, the conjecture is related to the recent work of Bley, Hahn, and the second author [Reference Bley, Burns and Hahn3] concerning metric structures arising from
![]() $A_\pi $
(for more details of which, see the Ph.D. thesis [Reference Kuang17] of the fourth author).
$A_\pi $
(for more details of which, see the Ph.D. thesis [Reference Kuang17] of the fourth author).
In this paper, we show that, in general, Conjecture 1.4 fails for tame extensions. For each tame extension
![]() $F_\pi /F$
, we use the signs at infinity of certain symplectic Galois–Jacobi sums to define an element
$F_\pi /F$
, we use the signs at infinity of certain symplectic Galois–Jacobi sums to define an element
![]() ${\mathcal J}^*_\infty (F_\pi /F) \in \operatorname {\mathrm {Cl}}({\mathbf Z} G)$
. The class
${\mathcal J}^*_\infty (F_\pi /F) \in \operatorname {\mathrm {Cl}}({\mathbf Z} G)$
. The class
![]() ${\mathcal J}^*_\infty (F_\pi /F)$
is of order at most
${\mathcal J}^*_\infty (F_\pi /F)$
is of order at most
![]() $2$
, and is often, but not always, equal to zero. We prove the following result.
$2$
, and is often, but not always, equal to zero. We prove the following result.
Theorem 1.5 Suppose that
![]() $F_{\pi }/F$
is tame and that
$F_{\pi }/F$
is tame and that
![]() $A_\pi $
exists. Then
$A_\pi $
exists. Then
i.e., (see (1.1))
Our proof of Theorem 1.5 combines methods from [Reference Agboola and Burns1, Reference Agboola and McCulloh2] involving relative algebraic K-theory with the use of non-abelian Galois–Jacobi sums, the explicit computation by Fröhlich and Queyrut of the local root numbers of dihedral representations and a detailed representation-theoretic analysis of the failure (in the relevant cases) of induction functors to commute with Adams operators. In particular, it is interesting to compare our use of Galois–Jacobi sums with the methods of [Reference Caputo and Vinatier4], where abelian Jacobi sums play a critical role.
Remark 1.6 It remains an open question as to whether (1.2) continues to hold if the tameness hypothesis is relaxed.
For any integer
![]() $m \geq 1$
, we write
$m \geq 1$
, we write
![]() $H_{4m}$
for the generalized quaternion group of order
$H_{4m}$
for the generalized quaternion group of order
![]() $4m$
. The following result, which is obtained by combining Theorem 1.5 with the work of Fröhlich on root numbers (see [Reference Fröhlich11]), gives infinitely many counterexamples to Conjecture 1.4.
$4m$
. The following result, which is obtained by combining Theorem 1.5 with the work of Fröhlich on root numbers (see [Reference Fröhlich11]), gives infinitely many counterexamples to Conjecture 1.4.
Theorem 1.7 Let F be an imaginary quadratic field such that
![]() $\operatorname {\mathrm {Cl}}(O_F)$
contains an element of order
$\operatorname {\mathrm {Cl}}(O_F)$
contains an element of order
![]() $4$
. Then, for any sufficiently large prime
$4$
. Then, for any sufficiently large prime
![]() $\ell $
with
$\ell $
with
![]() $\ell \equiv 3\ \pmod {4}$
, there are infinitely many tame,
$\ell \equiv 3\ \pmod {4}$
, there are infinitely many tame,
![]() $H_{4\ell }$
-extensions
$H_{4\ell }$
-extensions
![]() $F_\pi /F$
such that
$F_\pi /F$
such that
![]() $A_\pi $
exists and
$A_\pi $
exists and
![]() $(A_\pi ) \neq (O_\pi )$
in
$(A_\pi ) \neq (O_\pi )$
in
![]() $\operatorname {\mathrm {Cl}}({\mathbf Z} H_{4\ell })$
.
$\operatorname {\mathrm {Cl}}({\mathbf Z} H_{4\ell })$
.
An outline of the contents of this paper is as follows. In Section 2, we recall certain basic facts about relative algebraic K-theory from [Reference Agboola and Burns1, Reference Agboola and McCulloh2]. In Section 3, we discuss how ideals in Galois algebras give rise to elements in certain relative K-groups. Section 4 contains a description of the Stickelberger factorization of certain tame resolvends (see [Reference Agboola and McCulloh2, Section 7]) in the case of both rings of integers and square roots of inverse differents, while Section 5 develops properties of Stickelberger pairings and explains how these may be used to give explicit descriptions of the tame resolvends considered in the previous section. In Section 6, we recall a number of facts concerning Galois–Gauss sums. We define Galois–Jacobi sums, and we establish some of their basic properties. In Section 7, we compute the signs of local Galois–Jacobi sums at symplectic characters by combining an analysis of the behavior of Adams operators with respect to induction functors together with the theorem of Fröhlich and Queyrut. In Section 9, we prove Theorem 1.5. Finally, in Section 10, we prove Theorem 1.7.
Notation and conventions
For any field L, we write
![]() $L^c$
for an algebraic closure of L, and we set
$L^c$
for an algebraic closure of L, and we set
![]() $\Omega _L:= \operatorname {\mathrm {Gal}}(L^c/L)$
. If L is a number field or a non-archimedean local field (by which we shall always mean a finite extension of
$\Omega _L:= \operatorname {\mathrm {Gal}}(L^c/L)$
. If L is a number field or a non-archimedean local field (by which we shall always mean a finite extension of
![]() ${\mathbf Q}_p$
for some prime p), then
${\mathbf Q}_p$
for some prime p), then
![]() $O_L$
denotes the ring of integers of L. If L is an archimedean local field, then we adopt the usual convention of setting
$O_L$
denotes the ring of integers of L. If L is an archimedean local field, then we adopt the usual convention of setting
![]() $O_L = L$
.
$O_L = L$
.
Throughout this paper, F will denote a number field. For each place v of F, we fix an embedding
![]() $F^c \to F_{v}^{c}$
, and we view
$F^c \to F_{v}^{c}$
, and we view
![]() $\Omega _{F_v}$
as being a subgroup of
$\Omega _{F_v}$
as being a subgroup of
![]() $\Omega _F$
via this choice of embedding. We write
$\Omega _F$
via this choice of embedding. We write
![]() $I_v$
for the inertia subgroup of
$I_v$
for the inertia subgroup of
![]() $\Omega _{F_v}$
when v is finite.
$\Omega _{F_v}$
when v is finite.
If H is any finite group, we write
![]() $\operatorname {\mathrm {Irr}}(H)$
for the set of irreducible
$\operatorname {\mathrm {Irr}}(H)$
for the set of irreducible
![]() $F^c$
-valued characters of H and
$F^c$
-valued characters of H and
![]() $R_H$
for the corresponding ring of virtual characters. We write
$R_H$
for the corresponding ring of virtual characters. We write
![]() ${\mathbf 1}_H$
(or simply
${\mathbf 1}_H$
(or simply
![]() ${\mathbf 1}$
if there is no danger of confusion) for the trivial character in
${\mathbf 1}$
if there is no danger of confusion) for the trivial character in
![]() $R_H$
.
$R_H$
.
Let L be a number field or local field, and suppose that
![]() $\Gamma $
is any group on which
$\Gamma $
is any group on which
![]() $\Omega _L$
acts continuously. (We shall usually, but not always, be primarily concerned with the case of trivial
$\Omega _L$
acts continuously. (We shall usually, but not always, be primarily concerned with the case of trivial
![]() $\Omega _L$
-action; see below for further remarks on this.) We identify
$\Omega _L$
-action; see below for further remarks on this.) We identify
![]() $\Gamma $
-torsors over L (as well as their associated algebras, which are Hopf–Galois extensions associated with
$\Gamma $
-torsors over L (as well as their associated algebras, which are Hopf–Galois extensions associated with
![]() $A_{\Gamma }:= (L^c\Gamma )^{\Omega _{L}}$
) with elements of the set
$A_{\Gamma }:= (L^c\Gamma )^{\Omega _{L}}$
) with elements of the set
![]() $Z^1(\Omega _L, \Gamma )$
of
$Z^1(\Omega _L, \Gamma )$
of
![]() $\Gamma $
-valued continuous
$\Gamma $
-valued continuous
![]() $1$
-cocycles of
$1$
-cocycles of
![]() $\Omega _L$
(see [Reference Serre24, I.5.2]). If
$\Omega _L$
(see [Reference Serre24, I.5.2]). If
![]() $\pi \in Z^1(\Omega _L, \Gamma )$
, then we write
$\pi \in Z^1(\Omega _L, \Gamma )$
, then we write
![]() $L_\pi /L$
for the corresponding Hopf–Galois extension of L, and
$L_\pi /L$
for the corresponding Hopf–Galois extension of L, and
![]() $O_\pi $
for the integral closure of
$O_\pi $
for the integral closure of
![]() $O_L$
in
$O_L$
in
![]() $L_\pi $
. (Thus,
$L_\pi $
. (Thus,
![]() $O_{\pi } = L_{\pi }$
if L is an archimedean local field.) Each such
$O_{\pi } = L_{\pi }$
if L is an archimedean local field.) Each such
![]() $L_{\pi }$
is a principal homogeneous space of the Hopf algebra
$L_{\pi }$
is a principal homogeneous space of the Hopf algebra
![]() $\operatorname {\mathrm {Map}}_{\Omega _L}(\Gamma , L^c)$
of
$\operatorname {\mathrm {Map}}_{\Omega _L}(\Gamma , L^c)$
of
![]() $\Omega _L$
-equivariant maps from
$\Omega _L$
-equivariant maps from
![]() $\Gamma $
to
$\Gamma $
to
![]() $L^c$
. It may be shown that if
$L^c$
. It may be shown that if
![]() $\pi _1, \pi _2 \in Z^1(\Omega _L,\Gamma )$
, then
$\pi _1, \pi _2 \in Z^1(\Omega _L,\Gamma )$
, then
![]() $L_{\pi _1} \simeq L_{\pi _2}$
if and only if
$L_{\pi _1} \simeq L_{\pi _2}$
if and only if
![]() $\pi _1$
and
$\pi _1$
and
![]() $\pi _2$
differ by a coboundary. The set of isomorphism classes of
$\pi _2$
differ by a coboundary. The set of isomorphism classes of
![]() $\Gamma $
-torsors over L may be identified with the pointed cohomology set
$\Gamma $
-torsors over L may be identified with the pointed cohomology set
![]() $H^1(L,\Gamma ):=H^1(\Omega _L,\Gamma )$
. We write
$H^1(L,\Gamma ):=H^1(\Omega _L,\Gamma )$
. We write
![]() $[\pi ] \in H^1(L,\Gamma )$
for the class of
$[\pi ] \in H^1(L,\Gamma )$
for the class of
![]() $L_{\pi }$
in
$L_{\pi }$
in
![]() $H^1(L,\Gamma )$
. If L is a number field or a non-archimedean local field, we write
$H^1(L,\Gamma )$
. If L is a number field or a non-archimedean local field, we write
![]() $H^1_t(L,\Gamma )$
for the subset of
$H^1_t(L,\Gamma )$
for the subset of
![]() $H^1(L,\Gamma )$
consisting of those
$H^1(L,\Gamma )$
consisting of those
![]() $[\pi ] \in H^1(L,\Gamma )$
for which
$[\pi ] \in H^1(L,\Gamma )$
for which
![]() $L_{\pi }/L$
is at most tamely ramified. If L is an archimedean local field, we set
$L_{\pi }/L$
is at most tamely ramified. If L is an archimedean local field, we set
![]() $H^1_t(L,\Gamma ) = H^1(L, \Gamma )$
. We denote the subset of
$H^1_t(L,\Gamma ) = H^1(L, \Gamma )$
. We denote the subset of
![]() $H^1_t(L,\Gamma )$
consisting of those
$H^1_t(L,\Gamma )$
consisting of those
![]() $[\pi ] \in H^1_t(L,\Gamma )$
for which
$[\pi ] \in H^1_t(L,\Gamma )$
for which
![]() $L_{\pi }/L$
is unramified at all (including infinite) places of L by
$L_{\pi }/L$
is unramified at all (including infinite) places of L by
![]() $H^{1}_{nr}(L,\Gamma )$
. (So, with this convention, if L is an archimedean local field, we have
$H^{1}_{nr}(L,\Gamma )$
. (So, with this convention, if L is an archimedean local field, we have
![]() $H^{1}_{nr}(L, \Gamma ) = 0$
.)
$H^{1}_{nr}(L, \Gamma ) = 0$
.)
We remark that if
![]() $\Omega _L$
acts trivially on
$\Omega _L$
acts trivially on
![]() $\Gamma $
, then we recover classical Galois theory:
$\Gamma $
, then we recover classical Galois theory:
![]() $\pi $
is a homomorphism,
$\pi $
is a homomorphism,
![]() $L_{\pi }/L$
is simply an extension of
$L_{\pi }/L$
is simply an extension of
![]() $\Gamma $
-Galois algebras, and
$\Gamma $
-Galois algebras, and
![]() $L_{\pi }$
is a field if
$L_{\pi }$
is a field if
![]() $\pi $
is surjective. For the most part, this is the only case that will be needed in this paper. There is, however, one important exception. This occurs in Section 4 when we describe a certain decomposition (a Stickelberger factorization) of resolvends of normal basis generators of tame local extensions. (This is a non-abelian analogue of Stickelberger’s factorization of abelian Gauss sums. See [Reference Agboola and McCulloh2, Definition 7.2] for further remarks on this choice of terminology.)
$\pi $
is surjective. For the most part, this is the only case that will be needed in this paper. There is, however, one important exception. This occurs in Section 4 when we describe a certain decomposition (a Stickelberger factorization) of resolvends of normal basis generators of tame local extensions. (This is a non-abelian analogue of Stickelberger’s factorization of abelian Gauss sums. See [Reference Agboola and McCulloh2, Definition 7.2] for further remarks on this choice of terminology.)
If A is any algebra, we write
![]() $Z(A)$
for the center of A. If A is an R-algebra for some ring R, and
$Z(A)$
for the center of A. If A is an R-algebra for some ring R, and
![]() $R \to R_1$
is an extension of R, we write
$R \to R_1$
is an extension of R, we write
![]() $A_{R_1}:= A \otimes _{R} R_1$
to denote extension of scalars from R to
$A_{R_1}:= A \otimes _{R} R_1$
to denote extension of scalars from R to
![]() $R_1$
.
$R_1$
.
2 Relative algebraic K-theory
The purpose of this section is briefly to recall a number of basic facts concerning relative algebraic K-theory that we shall need. For a more extensive discussion of these topics, the reader is strongly encouraged to consult [Reference Agboola and McCulloh2, Section 5] as well as [Reference Agboola and Burns1, Sections 2 and 3] and [Reference Swan25, Chapter 15].
Let R be a Dedekind domain with field of fractions L of characteristic zero, and suppose that G is a finite group upon which
![]() $\Omega _L$
acts trivially. Let
$\Omega _L$
acts trivially. Let
![]() ${\mathfrak A}$
be any finitely generated R-algebra satisfying
${\mathfrak A}$
be any finitely generated R-algebra satisfying
![]() ${\mathfrak A} \otimes _R L \simeq LG$
.
${\mathfrak A} \otimes _R L \simeq LG$
.
For any extension
![]() $\Lambda $
of R, we write
$\Lambda $
of R, we write
![]() $K_0({\mathfrak A}, \Lambda )$
for the relative algebraic K-group that arises via the extension of scalars afforded by the map
$K_0({\mathfrak A}, \Lambda )$
for the relative algebraic K-group that arises via the extension of scalars afforded by the map
![]() $R \to \Lambda $
. Each element of
$R \to \Lambda $
. Each element of
![]() $K_0({\mathfrak A}, \Lambda )$
is represented by a triple
$K_0({\mathfrak A}, \Lambda )$
is represented by a triple
![]() $[M, N;\xi ]$
, where M and N are finitely generated, projective
$[M, N;\xi ]$
, where M and N are finitely generated, projective
![]() ${\mathfrak A}$
-modules, and
${\mathfrak A}$
-modules, and
![]() $\xi : M \otimes _{R} \Lambda \xrightarrow {\sim } N \otimes _R \Lambda $
is an isomorphism of
$\xi : M \otimes _{R} \Lambda \xrightarrow {\sim } N \otimes _R \Lambda $
is an isomorphism of
![]() ${\mathfrak A} \otimes _R \Lambda $
-modules.
${\mathfrak A} \otimes _R \Lambda $
-modules.
Recall that there is a long exact sequence of relative algebraic K-theory (see [Reference Swan25, Theorem 15.5])
The first and last arrows in this sequence are induced by the extension of scalars map
![]() $R \to \Lambda $
, whereas the map
$R \to \Lambda $
, whereas the map
![]() $\partial ^{0}_{{\mathfrak A}, \Lambda }$
sends the triple
$\partial ^{0}_{{\mathfrak A}, \Lambda }$
sends the triple
![]() $[M, N;\xi ]$
to the element
$[M, N;\xi ]$
to the element
![]() $[M] - [N] \in K_0({\mathfrak A})$
.
$[M] - [N] \in K_0({\mathfrak A})$
.
The map
![]() $\partial ^{1}_{{\mathfrak A}, \Lambda }$
is defined as follows. The group
$\partial ^{1}_{{\mathfrak A}, \Lambda }$
is defined as follows. The group
![]() $K_1({\mathfrak A} \otimes _R \Lambda )$
is generated by elements of the form
$K_1({\mathfrak A} \otimes _R \Lambda )$
is generated by elements of the form
![]() $(V,\phi )$
, where V is a finitely generated, free
$(V,\phi )$
, where V is a finitely generated, free
![]() ${\mathfrak A} \otimes _R \Lambda $
-module, and
${\mathfrak A} \otimes _R \Lambda $
-module, and
![]() $\phi : V \xrightarrow {\sim } V$
is an
$\phi : V \xrightarrow {\sim } V$
is an
![]() ${\mathfrak A} \otimes _R \Lambda $
-isomorphism. To define
${\mathfrak A} \otimes _R \Lambda $
-isomorphism. To define
![]() $\partial ^{1}_{{\mathfrak A}, \Lambda }((V,\phi ))$
, we choose any projective
$\partial ^{1}_{{\mathfrak A}, \Lambda }((V,\phi ))$
, we choose any projective
![]() ${\mathfrak A}$
-submodule T of V such that
${\mathfrak A}$
-submodule T of V such that
![]() $T \otimes _{{\mathfrak A}} \Lambda = V$
, and we set
$T \otimes _{{\mathfrak A}} \Lambda = V$
, and we set
It may be shown that this definition is independent of the choice of T.
Let
![]() $\operatorname {\mathrm {Cl}}({\mathfrak A})$
denote the locally free class group of
$\operatorname {\mathrm {Cl}}({\mathfrak A})$
denote the locally free class group of
![]() ${\mathfrak A}$
. If
${\mathfrak A}$
. If
![]() $\Lambda $
is a field (as will in fact always be the case in this paper), then (2.1) yields an exact sequence
$\Lambda $
is a field (as will in fact always be the case in this paper), then (2.1) yields an exact sequence
and this is the form of the long exact sequence of relative algebraic K-theory that we shall use in this paper.
We shall make heavy use of the fact that computations in relative K-groups and in locally free class groups may be carried out using functions on the characters of G. Suppose that L is either a number field or a local field, and write
![]() $R_G$
for the ring of virtual characters of G. The group
$R_G$
for the ring of virtual characters of G. The group
![]() $\Omega _L$
acts on
$\Omega _L$
acts on
![]() $R_G$
via the rule given by
$R_G$
via the rule given by
where
![]() $\omega \in \Omega _L$
,
$\omega \in \Omega _L$
,
![]() $\chi \in \operatorname {\mathrm {Irr}}(G)$
, and
$\chi \in \operatorname {\mathrm {Irr}}(G)$
, and
![]() $g \in G$
. For each element
$g \in G$
. For each element
![]() $a \in (L^cG)^{\times }$
, we define
$a \in (L^cG)^{\times }$
, we define
![]() $\operatorname {\mathrm {Det}}(a) \in \operatorname {\mathrm {Hom}}(R_G, (L^{c})^{\times })$
as follows. If T is any representation of G with character
$\operatorname {\mathrm {Det}}(a) \in \operatorname {\mathrm {Hom}}(R_G, (L^{c})^{\times })$
as follows. If T is any representation of G with character
![]() $\phi $
, then we set
$\phi $
, then we set
![]() $\operatorname {\mathrm {Det}}(a)(\phi ):= \det (T(a))$
. It may be shown that this definition is independent of the choice of representation T, and so depends only on the character
$\operatorname {\mathrm {Det}}(a)(\phi ):= \det (T(a))$
. It may be shown that this definition is independent of the choice of representation T, and so depends only on the character
![]() $\phi $
.
$\phi $
.
The map
![]() $\operatorname {\mathrm {Det}}$
is essentially the same as the reduced norm map
$\operatorname {\mathrm {Det}}$
is essentially the same as the reduced norm map
(see [Reference Agboola and McCulloh2, Remark 4.2]): (2.3) induces an isomorphism
and we have
![]() $\operatorname {\mathrm {Det}}(a)(\phi ) = \operatorname {\mathrm {nrd}}(a)(\phi )$
.
$\operatorname {\mathrm {Det}}(a)(\phi ) = \operatorname {\mathrm {nrd}}(a)(\phi )$
.
Suppose now that we are working over a number field F (i.e.,
![]() $L = F$
above). We define the group of finite ideles
$L = F$
above). We define the group of finite ideles
![]() $J_f(K_1(FG))$
to be the restricted direct product over all finite places v of F of the groups
$J_f(K_1(FG))$
to be the restricted direct product over all finite places v of F of the groups
![]() $\operatorname {\mathrm {Det}}(F_vG)^{\times } \simeq K_1(F_vG)$
with respect to the subgroups
$\operatorname {\mathrm {Det}}(F_vG)^{\times } \simeq K_1(F_vG)$
with respect to the subgroups
![]() $\operatorname {\mathrm {Det}}(O_{F_v}G)^{\times }$
. (We shall require no use of the infinite places of F in the idelic descriptions given below. See, e.g., [Reference Curtis and Reiner9, pp. 226–228] for details concerning this point.)
$\operatorname {\mathrm {Det}}(O_{F_v}G)^{\times }$
. (We shall require no use of the infinite places of F in the idelic descriptions given below. See, e.g., [Reference Curtis and Reiner9, pp. 226–228] for details concerning this point.)
For each finite place v of F, we write
for the obvious localisation map.
Let E be any extension of F. Then the homomorphism
induces a homomorphism
 $$\begin{align*}\Delta_{{\mathfrak A},E}: \operatorname{\mathrm{Det}}(FG)^{\times} \to \frac{J_{f}(K_1(FG))}{\prod_{v \nmid \infty} \operatorname{\mathrm{Det}}({\mathfrak A}_v)^{\times}} \times \operatorname{\mathrm{Det}}(EG)^{\times}. \end{align*}$$
$$\begin{align*}\Delta_{{\mathfrak A},E}: \operatorname{\mathrm{Det}}(FG)^{\times} \to \frac{J_{f}(K_1(FG))}{\prod_{v \nmid \infty} \operatorname{\mathrm{Det}}({\mathfrak A}_v)^{\times}} \times \operatorname{\mathrm{Det}}(EG)^{\times}. \end{align*}$$
Theorem 2.1 (a) There is a natural isomorphism
 $$\begin{align*}\operatorname{\mathrm{Cl}}({\mathfrak A}) \xrightarrow{\sim} \frac{J_{f}(K_1(FG))}{\operatorname{\mathrm{Det}}(FG)^{\times} \prod_{v \nmid \infty} \operatorname{\mathrm{Det}}({\mathfrak A}_v)^{\times}}. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Cl}}({\mathfrak A}) \xrightarrow{\sim} \frac{J_{f}(K_1(FG))}{\operatorname{\mathrm{Det}}(FG)^{\times} \prod_{v \nmid \infty} \operatorname{\mathrm{Det}}({\mathfrak A}_v)^{\times}}. \end{align*}$$
(b) There is a natural isomorphism
(c) Let v be a finite place of F, and suppose that
![]() $L_v$
is any extension of
$L_v$
is any extension of
![]() $F_v$
. Then there are isomorphisms
$F_v$
. Then there are isomorphisms
Proof Part (a) is due to Fröhlich (see, e.g., [Reference Fröhlich15, Chapter I] or [Reference Fröhlich12]). Part (b) is proved in [Reference Agboola and Burns1, Theorem 3.5], and a proof of part (c) is given in [Reference Agboola and McCulloh2, Lemma 5.7].
Remark 2.2 Suppose that
![]() $x \in K_0({\mathfrak A}, E)$
is represented by the idele
$x \in K_0({\mathfrak A}, E)$
is represented by the idele
![]() $[(x_{v})_{v}, x_{\infty }] \in J_{f}(K_1(FG)) \times \operatorname {\mathrm {Det}}(EG)^{\times }$
. Then
$[(x_{v})_{v}, x_{\infty }] \in J_{f}(K_1(FG)) \times \operatorname {\mathrm {Det}}(EG)^{\times }$
. Then
![]() $\partial ^0(x) \in \operatorname {\mathrm {Cl}}({\mathfrak A})$
is represented by the idele
$\partial ^0(x) \in \operatorname {\mathrm {Cl}}({\mathfrak A})$
is represented by the idele
![]() $(x_{v})_{v} \in J_{f}(K_1(FG))$
.
$(x_{v})_{v} \in J_{f}(K_1(FG))$
.
Remark 2.3 Suppose that
![]() $[M,N;\xi ] \in K_0(O_FG, E)$
and that M and N are locally free
$[M,N;\xi ] \in K_0(O_FG, E)$
and that M and N are locally free
![]() ${\mathfrak A}$
-modules of rank one. An explicit representative in
${\mathfrak A}$
-modules of rank one. An explicit representative in
![]() $J_{f}(K_1(FG)) \times \operatorname {\mathrm {Det}}(EG)^{\times }$
of
$J_{f}(K_1(FG)) \times \operatorname {\mathrm {Det}}(EG)^{\times }$
of
![]() $h_{{\mathfrak A},E}([M,N;\xi ])$
may be constructed as follows.
$h_{{\mathfrak A},E}([M,N;\xi ])$
may be constructed as follows.
For each finite place v of F, fix
![]() ${\mathfrak A}_v$
-bases
${\mathfrak A}_v$
-bases
![]() $m_v$
of
$m_v$
of
![]() $M_v$
and
$M_v$
and
![]() $n_v$
of
$n_v$
of
![]() $N_v$
. Fix also an
$N_v$
. Fix also an
![]() $FG$
-basis
$FG$
-basis
![]() $n_{\infty }$
of
$n_{\infty }$
of
![]() $N_F$
, and choose an isomorphism
$N_F$
, and choose an isomorphism
![]() $\theta : M_F \xrightarrow {\sim } N_F$
of
$\theta : M_F \xrightarrow {\sim } N_F$
of
![]() $FG$
-modules.
$FG$
-modules.
The element
![]() $\theta ^{-1}(n_{\infty })$
is an
$\theta ^{-1}(n_{\infty })$
is an
![]() $FG$
-basis of
$FG$
-basis of
![]() $M_F$
. Hence, for each place v, we may write
$M_F$
. Hence, for each place v, we may write
 $$ \begin{align*} m_v &= \mu_v \cdot \theta^{-1}(n_{\infty}), \\ n_v &= \nu_v \cdot n_{\infty}, \end{align*} $$
$$ \begin{align*} m_v &= \mu_v \cdot \theta^{-1}(n_{\infty}), \\ n_v &= \nu_v \cdot n_{\infty}, \end{align*} $$
where
![]() $\mu _v, \nu _v \in (F_vG)^{\times }$
.
$\mu _v, \nu _v \in (F_vG)^{\times }$
.
If we write
![]() $\theta _E: M_E \xrightarrow {\sim } N_E$
for the isomorphism afforded by
$\theta _E: M_E \xrightarrow {\sim } N_E$
for the isomorphism afforded by
![]() $\theta $
via extension of scalars, then we see that the isomorphism
$\theta $
via extension of scalars, then we see that the isomorphism
![]() $\xi \circ \theta ^{-1}_{E}: N_E \xrightarrow {\sim } N_E$
is given by
$\xi \circ \theta ^{-1}_{E}: N_E \xrightarrow {\sim } N_E$
is given by
![]() $n_{\infty } \mapsto \nu _{\infty } \cdot n_{\infty }$
for some
$n_{\infty } \mapsto \nu _{\infty } \cdot n_{\infty }$
for some
![]() $\nu _{\infty } \in (EG)^{\times }$
.
$\nu _{\infty } \in (EG)^{\times }$
.
A representative of
![]() $h_{{\mathfrak A},E}([M,N;\xi ])$
is given by the image of
$h_{{\mathfrak A},E}([M,N;\xi ])$
is given by the image of
![]() $[(\mu _v \cdot \nu ^{-1}_{v})_{v}, \nu _{\infty }]$
in
$[(\mu _v \cdot \nu ^{-1}_{v})_{v}, \nu _{\infty }]$
in
![]() $J_{f}(K_1(FG)) \times \operatorname {\mathrm {Det}}(EG)^{\times }$
.
$J_{f}(K_1(FG)) \times \operatorname {\mathrm {Det}}(EG)^{\times }$
.
Remark 2.4 We see from Theorem 2.1(b) and (c) that there are isomorphisms
 $$\begin{align*}K_0({\mathfrak A}, F) \simeq \frac{J_{f}(K_1(FG))}{\prod_{v \nmid \infty} \operatorname{\mathrm{Det}}({\mathfrak A}_{v})^{\times}} \simeq \frac{\operatorname{\mathrm{Hom}}_{\Omega_F}(R_G, J_{f}(F^c))}{\prod_{v \nmid \infty} \operatorname{\mathrm{Det}}({\mathfrak A}_{v})^{\times}} \simeq \oplus_{v \nmid \infty} K_{0}({\mathfrak A}_{v}, F_{v}). \end{align*}$$
$$\begin{align*}K_0({\mathfrak A}, F) \simeq \frac{J_{f}(K_1(FG))}{\prod_{v \nmid \infty} \operatorname{\mathrm{Det}}({\mathfrak A}_{v})^{\times}} \simeq \frac{\operatorname{\mathrm{Hom}}_{\Omega_F}(R_G, J_{f}(F^c))}{\prod_{v \nmid \infty} \operatorname{\mathrm{Det}}({\mathfrak A}_{v})^{\times}} \simeq \oplus_{v \nmid \infty} K_{0}({\mathfrak A}_{v}, F_{v}). \end{align*}$$
There is a natural injection
 $$\begin{align*} K_0({\mathfrak A}, F) &\to K_0({\mathfrak A}, F^c) \\ [M,N;\xi] &\mapsto [M,N;\xi_{F^{c}}], \end{align*}$$
$$\begin{align*} K_0({\mathfrak A}, F) &\to K_0({\mathfrak A}, F^c) \\ [M,N;\xi] &\mapsto [M,N;\xi_{F^{c}}], \end{align*}$$
where
![]() $\xi _{F^c}: M_{F^c} \xrightarrow {\sim } N_{F^c}$
is the isomorphism obtained from
$\xi _{F^c}: M_{F^c} \xrightarrow {\sim } N_{F^c}$
is the isomorphism obtained from
![]() $\xi :M_F \xrightarrow {\sim } N_{F}$
via extension of scalars from F to
$\xi :M_F \xrightarrow {\sim } N_{F}$
via extension of scalars from F to
![]() $F^c$
. It is not hard to check that this map is induced by the inclusion map
$F^c$
. It is not hard to check that this map is induced by the inclusion map
 $$\begin{align*} J_{f}(K_1(FG)) &\to J_{f}(K_1(FG)) \times \operatorname{\mathrm{Det}}(F^{c}G)^{\times} \\ (x_{v})_{v} &\mapsto [(x_{v})_{v}, 1]. \end{align*}$$
$$\begin{align*} J_{f}(K_1(FG)) &\to J_{f}(K_1(FG)) \times \operatorname{\mathrm{Det}}(F^{c}G)^{\times} \\ (x_{v})_{v} &\mapsto [(x_{v})_{v}, 1]. \end{align*}$$
We now recall the description of the restriction of scalars map on relative K-groups and locally free class groups in terms of the isomorphism given by Theorem 2.1(b).
Suppose that
![]() ${\mathcal F}/F$
is a finite extension and that E is an extension of
${\mathcal F}/F$
is a finite extension and that E is an extension of
![]() ${\mathcal F}$
. Then restriction of scalars from
${\mathcal F}$
. Then restriction of scalars from
![]() $O_{{\mathcal F}}$
to
$O_{{\mathcal F}}$
to
![]() $O_F$
yields homomorphisms
$O_F$
yields homomorphisms
and
which may be described as follows (see, e.g., [Reference Fröhlich15, Chapter IV] or [Reference Taylor27, Chapter 1]).
Let
![]() $\{\omega \}$
be any transversal of
$\{\omega \}$
be any transversal of
![]() $\Omega _{{\mathcal F}} \backslash \Omega _F$
. Then the map
$\Omega _{{\mathcal F}} \backslash \Omega _F$
. Then the map
 $$ \begin{align*} J_{f}(K_1({\mathcal F} G)) \times \operatorname{\mathrm{Det}}(EG)^{\times} &\to J_{f}(K_1(FG)) \times \operatorname{\mathrm{Det}}(EG)^{\times}\\ [(y_v)_v, y_{\infty}] &\mapsto \prod_{\omega} [(y_v)_v, y_{\infty}]^{\omega} \end{align*} $$
$$ \begin{align*} J_{f}(K_1({\mathcal F} G)) \times \operatorname{\mathrm{Det}}(EG)^{\times} &\to J_{f}(K_1(FG)) \times \operatorname{\mathrm{Det}}(EG)^{\times}\\ [(y_v)_v, y_{\infty}] &\mapsto \prod_{\omega} [(y_v)_v, y_{\infty}]^{\omega} \end{align*} $$
induces homomorphisms
and
These homomorphisms are independent of the choice of
![]() $\{\omega \}$
and are equal to the natural maps on relative K-groups (resp. locally free class groups) afforded by restriction of scalars from
$\{\omega \}$
and are equal to the natural maps on relative K-groups (resp. locally free class groups) afforded by restriction of scalars from
![]() $O_{{\mathcal F}}$
to
$O_{{\mathcal F}}$
to
![]() $O_F$
.
$O_F$
.
We conclude this section by recalling the definitions of certain induction maps on relative algebraic K-groups and on locally free class groups of group rings (see, e.g., [Reference Fröhlich15, Chapter II] or [Reference Taylor27, Chapter I]).
Suppose that G is a finite group and that H is a subgroup of G. Let E be an algebraic extension of F. Then extension of scalars from
![]() $O_FH$
to
$O_FH$
to
![]() $O_FG$
yields natural homomorphisms
$O_FG$
yields natural homomorphisms
and
It may be shown that these homomorphisms are induced (via the isomorphisms described in Theorem 2.1) by the maps
 $$ \begin{align*} &\operatorname{\mathrm{Ind}}^G_H: \operatorname{\mathrm{Hom}}(R_H, J(F^c)) \to \operatorname{\mathrm{Hom}}(R_G, J(F^c)), \\ &\operatorname{\mathrm{Ind}}^G_H:\operatorname{\mathrm{Hom}}(R_H, (F^{c})^{\times}) \to \operatorname{\mathrm{Hom}}(R_G, (F^{c})^{\times}) \end{align*} $$
$$ \begin{align*} &\operatorname{\mathrm{Ind}}^G_H: \operatorname{\mathrm{Hom}}(R_H, J(F^c)) \to \operatorname{\mathrm{Hom}}(R_G, J(F^c)), \\ &\operatorname{\mathrm{Ind}}^G_H:\operatorname{\mathrm{Hom}}(R_H, (F^{c})^{\times}) \to \operatorname{\mathrm{Hom}}(R_G, (F^{c})^{\times}) \end{align*} $$
given by
It is not hard to check from the definitions that the following diagram commutes:

3 Galois algebras and ideals
Let L be either a number field or a local field, and suppose that
![]() $\pi \in Z^1(\Omega _L, G)$
is a continuous G-valued
$\pi \in Z^1(\Omega _L, G)$
is a continuous G-valued
![]() $\Omega _L$
$\Omega _L$
![]() $1$
-cocycle. We may define an associated G-Galois L-algebra
$1$
-cocycle. We may define an associated G-Galois L-algebra
![]() $L_{\pi }$
by
$L_{\pi }$
by
where
![]() $^{\pi }G$
denotes the set G endowed with an action of
$^{\pi }G$
denotes the set G endowed with an action of
![]() $\Omega _L$
via the cocycle
$\Omega _L$
via the cocycle
![]() $\pi $
(i.e.,
$\pi $
(i.e.,
![]() $g^{\omega } = \pi (\omega ) \cdot g$
for
$g^{\omega } = \pi (\omega ) \cdot g$
for
![]() $g \in {^{\pi }G}$
and
$g \in {^{\pi }G}$
and
![]() $\omega \in \Omega _L$
), and
$\omega \in \Omega _L$
), and
![]() $L_{\pi }$
is the algebra of
$L_{\pi }$
is the algebra of
![]() $L^c$
-valued functions on
$L^c$
-valued functions on
![]() $^{\pi }G$
that are fixed under the action of
$^{\pi }G$
that are fixed under the action of
![]() $\Omega _L$
. The group G acts on
$\Omega _L$
. The group G acts on
![]() $L_{\pi }$
via the rule
$L_{\pi }$
via the rule
for all
![]() $g \in G$
and
$g \in G$
and
![]() $h \in {^{\pi }G}$
.
$h \in {^{\pi }G}$
.
The Wedderburn decomposition of the algebra
![]() $L_{\pi }$
may be described as follows. Set
$L_{\pi }$
may be described as follows. Set
so
![]() $\operatorname {\mathrm {Gal}}(L^{\pi }/L) \simeq \pi (\Omega _L)$
. Then
$\operatorname {\mathrm {Gal}}(L^{\pi }/L) \simeq \pi (\Omega _L)$
. Then
and this isomorphism depends only on the choice of a transversal of
![]() $\pi (\Omega _L)$
in G. It may be shown that every G-Galois L-algebra is of the form
$\pi (\Omega _L)$
in G. It may be shown that every G-Galois L-algebra is of the form
![]() $L_{\pi }$
for some
$L_{\pi }$
for some
![]() $\pi $
and that
$\pi $
and that
![]() $L_{\pi }$
is determined up to isomorphism by the class
$L_{\pi }$
is determined up to isomorphism by the class
![]() $[\pi ]$
of
$[\pi ]$
of
![]() $\pi $
in the pointed cohomology set
$\pi $
in the pointed cohomology set
![]() $H^1(L, G)$
. In particular, every Galois algebra may be viewed as being a subalgebra of the
$H^1(L, G)$
. In particular, every Galois algebra may be viewed as being a subalgebra of the
![]() $L^c$
-algebra
$L^c$
-algebra
![]() $\operatorname {\mathrm {Map}}(G, L^c)$
.
$\operatorname {\mathrm {Map}}(G, L^c)$
.
Definition 3.1 The resolvend map
![]() ${\mathbf r}_G$
on
${\mathbf r}_G$
on
![]() $\operatorname {\mathrm {Map}}(G, L^c)$
is defined as
$\operatorname {\mathrm {Map}}(G, L^c)$
is defined as
 $$ \begin{align*} {\mathbf r}_G: \operatorname{\mathrm{Map}}(G, L^c) &\rightarrow L^cG \\ a &\mapsto \sum_{g \in G} a(g) \cdot g^{-1}. \end{align*} $$
$$ \begin{align*} {\mathbf r}_G: \operatorname{\mathrm{Map}}(G, L^c) &\rightarrow L^cG \\ a &\mapsto \sum_{g \in G} a(g) \cdot g^{-1}. \end{align*} $$
(This is an isomorphism of
![]() $L^cG$
-modules, but it is not an isomorphism of
$L^cG$
-modules, but it is not an isomorphism of
![]() $L^c$
-algebras because it does not preserve multiplication.)
$L^c$
-algebras because it does not preserve multiplication.)
Suppose now that
![]() $L_{\pi }/L$
is a G-extension and that
$L_{\pi }/L$
is a G-extension and that
![]() ${\mathcal L} \subseteq L_{\pi }$
is a nonzero projective
${\mathcal L} \subseteq L_{\pi }$
is a nonzero projective
![]() $O_LG$
-module. Then there are isomorphisms
$O_LG$
-module. Then there are isomorphisms
and so the triple
![]() $[{\mathcal L}, O_LG; {\mathbf r}_G]$
yields an element of
$[{\mathcal L}, O_LG; {\mathbf r}_G]$
yields an element of
![]() $K_0(O_LG, L^c)$
.
$K_0(O_LG, L^c)$
.
Proposition 3.2 Let
![]() $F_{\pi }/F$
be a G-extension of a number field F, and suppose that
$F_{\pi }/F$
be a G-extension of a number field F, and suppose that
![]() ${\mathcal L}_i \subseteq F_{\pi }$
(
${\mathcal L}_i \subseteq F_{\pi }$
(
![]() $i =1,2$
) are nonzero projective
$i =1,2$
) are nonzero projective
![]() $O_FG$
-modules. For each place v of F, choose a basis
$O_FG$
-modules. For each place v of F, choose a basis
![]() $l_{i,v}$
of
$l_{i,v}$
of
![]() ${\mathcal L}_{i,v}$
over
${\mathcal L}_{i,v}$
over
![]() $O_{F_v}G$
, as well as a basis
$O_{F_v}G$
, as well as a basis
![]() $l_{\infty }$
of
$l_{\infty }$
of
![]() $F_{\pi }$
over
$F_{\pi }$
over
![]() $FG$
.
$FG$
.
-
(a) The element
 $[{\mathcal L}_i, O_FG; {\mathbf r}_G] \in K_0(O_FG, F^c)$
is represented by the image of the idele
$[{\mathcal L}_i, O_FG; {\mathbf r}_G] \in K_0(O_FG, F^c)$
is represented by the image of the idele
 $[({\mathbf r}_G(l_{i,v}) \cdot {\mathbf r}_G(l_{\infty })^{-1})_v, {\mathbf r}_G(l_{\infty })^{-1}] \in J_{f}(K_1(FG)) \times \operatorname {\mathrm {Det}}(F^cG)^{\times }$
.
$[({\mathbf r}_G(l_{i,v}) \cdot {\mathbf r}_G(l_{\infty })^{-1})_v, {\mathbf r}_G(l_{\infty })^{-1}] \in J_{f}(K_1(FG)) \times \operatorname {\mathrm {Det}}(F^cG)^{\times }$
. -
(b) The element
is represented by the image of the idele $$\begin{align*}[{\mathcal L}_1, O_FG; {\mathbf r}_G] - [{\mathcal L}_2, O_FG; {\mathbf r}_G] \in K_0(O_FG, F^c) \end{align*}$$
$$\begin{align*}[{\mathcal L}_1, O_FG; {\mathbf r}_G] - [{\mathcal L}_2, O_FG; {\mathbf r}_G] \in K_0(O_FG, F^c) \end{align*}$$
 $$\begin{align*}[({\mathbf r}_G(l_{1,v}) \cdot {\mathbf r}_G(l_{2,v}^{-1}))_v, 1] \in J_{f}(K_1(FG)) \times \operatorname{\mathrm{Det}}(F^cG)^{\times}. \end{align*}$$
$$\begin{align*}[({\mathbf r}_G(l_{1,v}) \cdot {\mathbf r}_G(l_{2,v}^{-1}))_v, 1] \in J_{f}(K_1(FG)) \times \operatorname{\mathrm{Det}}(F^cG)^{\times}. \end{align*}$$
-
(c) We have that
 $$\begin{align*}[{\mathcal L}_1, O_FG; {\mathbf r}_G] - [{\mathcal L}_2, O_FG; {\mathbf r}_G] \in K_0(O_FG, F) \subseteq K_0(O_FG, F^c). \end{align*}$$
$$\begin{align*}[{\mathcal L}_1, O_FG; {\mathbf r}_G] - [{\mathcal L}_2, O_FG; {\mathbf r}_G] \in K_0(O_FG, F) \subseteq K_0(O_FG, F^c). \end{align*}$$
Proof For each finite place v of F, write
with
![]() $x_{i,v} \in (F_vG)^{\times }$
. Then it follows from Remark 2.3 that
$x_{i,v} \in (F_vG)^{\times }$
. Then it follows from Remark 2.3 that
![]() $[{\mathcal L}_i, O_FG; {\mathbf r}_G] \in K_0(O_FG, F^c)$
is represented by the image of the idele
$[{\mathcal L}_i, O_FG; {\mathbf r}_G] \in K_0(O_FG, F^c)$
is represented by the image of the idele
![]() $[(x_{i,v})_{v}, {\mathbf r}_G(l_{\infty })^{-1}] \in J_{f}(K_1(FG)) \times \operatorname {\mathrm {Det}}(F^cG)^{\times }$
. However,
$[(x_{i,v})_{v}, {\mathbf r}_G(l_{\infty })^{-1}] \in J_{f}(K_1(FG)) \times \operatorname {\mathrm {Det}}(F^cG)^{\times }$
. However,
(because the resolvend map is an isomorphism of
![]() $F^cG$
and
$F^cG$
and
![]() $F^{c}_{v}G$
-modules), and this implies (a). Part (b) now follows directly from (a).
$F^{c}_{v}G$
-modules), and this implies (a). Part (b) now follows directly from (a).
To show part (c), we first recall that
and that an element
![]() $c \in K_0(O_FG, F^c)$
lies in
$c \in K_0(O_FG, F^c)$
lies in
![]() $K_0(O_FG, F)$
if it has an idelic representative lying in
$K_0(O_FG, F)$
if it has an idelic representative lying in
![]() $J_{f}(K_1(FG)) \times \operatorname {\mathrm {Det}}(FG)^{\times } \subseteq J_{f}(K_1(FG)) \times \operatorname {\mathrm {Det}}(F^cG)^{\times }$
(see Remark 2.4).
$J_{f}(K_1(FG)) \times \operatorname {\mathrm {Det}}(FG)^{\times } \subseteq J_{f}(K_1(FG)) \times \operatorname {\mathrm {Det}}(F^cG)^{\times }$
(see Remark 2.4).
Now, a standard property of resolvends implies that
for every
![]() $\omega \in \Omega _{F_v}$
(see, e.g., [Reference Agboola and McCulloh2, 2.2]), and so we see that
$\omega \in \Omega _{F_v}$
(see, e.g., [Reference Agboola and McCulloh2, 2.2]), and so we see that
![]() $({\mathbf r}_G(l_{1,v}) \cdot {\mathbf r}_G(l_{2,v}^{-1}))_v \in (F_vG)^{\times }$
for each v. (In fact, as we may take
$({\mathbf r}_G(l_{1,v}) \cdot {\mathbf r}_G(l_{2,v}^{-1}))_v \in (F_vG)^{\times }$
for each v. (In fact, as we may take
![]() $l_{1,v} = l_{2,v}$
for almost all v, we may suppose that
$l_{1,v} = l_{2,v}$
for almost all v, we may suppose that
![]() $({\mathbf r}_G(l_{1,v}) \cdot {\mathbf r}_G(l_{2,v}^{-1}))_v =1$
for almost all v.) Hence, it now follows from (b) that
$({\mathbf r}_G(l_{1,v}) \cdot {\mathbf r}_G(l_{2,v}^{-1}))_v =1$
for almost all v.) Hence, it now follows from (b) that
![]() $[{\mathcal L}_1, O_FG; F^c] - [{\mathcal L}_2, O_FG; F^c] \in K_0(O_FG, F) $
, as claimed.
$[{\mathcal L}_1, O_FG; F^c] - [{\mathcal L}_2, O_FG; F^c] \in K_0(O_FG, F) $
, as claimed.
It is a classical result, due to E. Noether, that a G-extension
![]() $F_{\pi }/F$
is tamely ramified if and only if
$F_{\pi }/F$
is tamely ramified if and only if
![]() $O_{\pi }$
is a locally free (and therefore projective)
$O_{\pi }$
is a locally free (and therefore projective)
![]() $O_FG$
-module. Ullom has shown that if
$O_FG$
-module. Ullom has shown that if
![]() $F_{\pi }/F$
is tame, then in fact all G-stable ideals in
$F_{\pi }/F$
is tame, then in fact all G-stable ideals in
![]() $O_{\pi }$
are locally free. He also showed that if any G-stable ideal B, say, in a G-extension
$O_{\pi }$
are locally free. He also showed that if any G-stable ideal B, say, in a G-extension
![]() $F_{\pi }/F$
is locally free, then all second ramification groups at primes dividing B are equal to zero (see [Reference Ullom29]). If
$F_{\pi }/F$
is locally free, then all second ramification groups at primes dividing B are equal to zero (see [Reference Ullom29]). If
![]() $F_{\pi }/F$
is any G-extension for which
$F_{\pi }/F$
is any G-extension for which
![]() $|G|$
is odd (and so the square root
$|G|$
is odd (and so the square root
![]() $A_\pi $
of the inverse different automatically exists), then Erez has shown that
$A_\pi $
of the inverse different automatically exists), then Erez has shown that
![]() $A_\pi $
is a locally free
$A_\pi $
is a locally free
![]() $O_FG$
-module if and only if all second ramification groups associated with
$O_FG$
-module if and only if all second ramification groups associated with
![]() $F_{\pi }/F$
vanish, i.e., if and only if
$F_{\pi }/F$
vanish, i.e., if and only if
![]() $F_{\pi }/F$
is weakly ramified. In fact, as pointed out by the third author and Vinatier [Reference Caputo and Vinatier4, p. 109, footnote 1], the proof of [Reference Erez10, Theorem 1] shows that if
$F_{\pi }/F$
is weakly ramified. In fact, as pointed out by the third author and Vinatier [Reference Caputo and Vinatier4, p. 109, footnote 1], the proof of [Reference Erez10, Theorem 1] shows that if
![]() $F_{\pi }/F$
is any weakly ramified extension such that
$F_{\pi }/F$
is any weakly ramified extension such that
![]() $A_{\pi }$
exists, then
$A_{\pi }$
exists, then
![]() $A_{\pi }$
is locally free.
$A_{\pi }$
is locally free.
Definition 3.3 Suppose that
![]() $[\pi ] \in H^{1}_{t}(F,G)$
and that
$[\pi ] \in H^{1}_{t}(F,G)$
and that
![]() $A_\pi $
exists. We define
$A_\pi $
exists. We define
4 Local decomposition of tame resolvends
Our goal in this section is to recall certain facts from [Reference Agboola and McCulloh2, Section 7] concerning Stickelberger factorizations of resolvends of normal integral basis generators of tame local extensions, and to describe similar results concerning resolvends of basis generators of the square root of the inverse different (when this exists). Roughly speaking, the underlying idea is that any tame Galois extension of local fields arises as the compositum of an unramified field extension with a totally ramified Hopf–Galois extension (which, in particular, need not be normal).
Let L be a local field, and fix a uniformizer
![]() ${\varpi } = {\varpi }_L$
of L. Set
${\varpi } = {\varpi }_L$
of L. Set
![]() $q:= |O_L/{\varpi }_L O_L|$
.
$q:= |O_L/{\varpi }_L O_L|$
.
Fix also a compatible set of roots of unity
![]() $\{ \zeta _m \}$
, and a compatible set
$\{ \zeta _m \}$
, and a compatible set
![]() $\{ {\varpi }^{1/m} \}$
of roots of
$\{ {\varpi }^{1/m} \}$
of roots of
![]() ${\varpi }$
. (Hence, if m and n are any two positive integers, then we have
${\varpi }$
. (Hence, if m and n are any two positive integers, then we have
![]() $(\zeta _{mn})^m = \zeta _n$
, and
$(\zeta _{mn})^m = \zeta _n$
, and
![]() $({\varpi }^{1/mn})^{m} = {\varpi }^{1/n}$
.)
$({\varpi }^{1/mn})^{m} = {\varpi }^{1/n}$
.)
Let
![]() $L^{nr}$
(resp.
$L^{nr}$
(resp.
![]() $L^{t}$
) denote the maximal unramified (resp. tamely ramified) extension of L. Then
$L^{t}$
) denote the maximal unramified (resp. tamely ramified) extension of L. Then
 $$\begin{align*}L^{nr}= \bigcup_{\stackrel{m \geq 1}{(m,q)=1}} L(\zeta_m),\quad L^t = \bigcup_{\stackrel{m \geq 1}{(m,q)=1}} L(\zeta_m, {\varpi}^{1/m}). \end{align*}$$
$$\begin{align*}L^{nr}= \bigcup_{\stackrel{m \geq 1}{(m,q)=1}} L(\zeta_m),\quad L^t = \bigcup_{\stackrel{m \geq 1}{(m,q)=1}} L(\zeta_m, {\varpi}^{1/m}). \end{align*}$$
The group
![]() $\Omega ^{nr}:= \operatorname {\mathrm {Gal}}(L^{nr}/L)$
is topologically generated by a Frobenius element
$\Omega ^{nr}:= \operatorname {\mathrm {Gal}}(L^{nr}/L)$
is topologically generated by a Frobenius element
![]() $\phi \in \operatorname {\mathrm {Gal}}(L^t/L)$
which may be chosen to satisfy
$\phi \in \operatorname {\mathrm {Gal}}(L^t/L)$
which may be chosen to satisfy
for each integer m coprime to q. Our choice of compatible roots of unity also uniquely specifies a topological generator
![]() $\sigma $
of
$\sigma $
of
![]() $\Omega ^r := \operatorname {\mathrm {Gal}}(L^t/L^{nr})$
by the conditions
$\Omega ^r := \operatorname {\mathrm {Gal}}(L^t/L^{nr})$
by the conditions
for all integers m coprime to q. The group
![]() $\Omega ^{t}:=\operatorname {\mathrm {Gal}}(L^{t}/L)$
is topologically generated by
$\Omega ^{t}:=\operatorname {\mathrm {Gal}}(L^{t}/L)$
is topologically generated by
![]() $\phi $
and
$\phi $
and
![]() $\sigma $
, subject to the relation
$\sigma $
, subject to the relation
The reader may find it helpful to keep in mind the following explicit example, due to Tsang (cf. [Reference Tsang28, Proposition 4.2.2]), while reading the next two sections.
Example 4.1 (Tsang)
Suppose that L contains the eth roots of unity with
![]() $(e,q)=1$
, and set
$(e,q)=1$
, and set
![]() $M := L({\varpi }_{L}^{1/e})$
. Write
$M := L({\varpi }_{L}^{1/e})$
. Write
![]() ${\varpi }_M := {\varpi }_{L}^{1/e}$
, then
${\varpi }_M := {\varpi }_{L}^{1/e}$
, then
![]() ${\varpi }_M$
is a uniformizer of M. Set
${\varpi }_M$
is a uniformizer of M. Set
![]() $H := \operatorname {\mathrm {Gal}}(M/L) = \langle s \rangle $
, say.
$H := \operatorname {\mathrm {Gal}}(M/L) = \langle s \rangle $
, say.
Let n be an integer with
![]() $0 \leq |n| \leq e-1$
, and let us consider the ideal
$0 \leq |n| \leq e-1$
, and let us consider the ideal
as an
![]() $O_LH$
-module. Set
$O_LH$
-module. Set
 $$\begin{align*}\alpha = \frac{1}{e}\sum_{i=0}^{e-1} {\varpi}_{M}^{n+i} = \frac{1}{e}\sum_{i=0}^{e-1} {\varpi}_{L}^{(n+i)/e}. \end{align*}$$
$$\begin{align*}\alpha = \frac{1}{e}\sum_{i=0}^{e-1} {\varpi}_{M}^{n+i} = \frac{1}{e}\sum_{i=0}^{e-1} {\varpi}_{L}^{(n+i)/e}. \end{align*}$$
We wish to explain why
and to give some motivation for the definition of the Stickelberger pairings in Definition 5.1.
Suppose that
![]() $s({\varpi }_M) = \zeta \cdot {\varpi }_M$
, where
$s({\varpi }_M) = \zeta \cdot {\varpi }_M$
, where
![]() $\zeta $
is a primitive eth root of unity. Then, for each
$\zeta $
is a primitive eth root of unity. Then, for each
![]() $0 \leq j \leq e-1$
, we have
$0 \leq j \leq e-1$
, we have
 $$\begin{align*}s^j(\alpha) = \frac{1}{e}\sum_{i=0}^{e-1}\zeta^{(i+n)j} {\varpi}_M^{i+n}. \end{align*}$$
$$\begin{align*}s^j(\alpha) = \frac{1}{e}\sum_{i=0}^{e-1}\zeta^{(i+n)j} {\varpi}_M^{i+n}. \end{align*}$$
Multiplying both sides of this last equality by
![]() $\zeta ^{-(l+n)j}$
, where
$\zeta ^{-(l+n)j}$
, where
![]() $0 \leq l \leq e-1$
, gives
$0 \leq l \leq e-1$
, gives
 $$\begin{align*}s^j(\alpha) \zeta^{-(l+n)j} = \frac{1}{e} \sum^{e-1}_{i=0} \zeta^{(i-l)j} {\varpi}_{M}^{i+n}. \end{align*}$$
$$\begin{align*}s^j(\alpha) \zeta^{-(l+n)j} = \frac{1}{e} \sum^{e-1}_{i=0} \zeta^{(i-l)j} {\varpi}_{M}^{i+n}. \end{align*}$$
Now, sum over j to obtain
 $$\begin{align*}\sum_{j=0}^{e-1} s^j(\alpha) \zeta^{-(l+n)j} = \frac{1}{e} \sum_{i=0}^{n} {\varpi}_{M}^{i+n} \sum_{j=0}^{e-1} \zeta^{(i-l)j} = {\varpi}_{M}^{l+n}. \end{align*}$$
$$\begin{align*}\sum_{j=0}^{e-1} s^j(\alpha) \zeta^{-(l+n)j} = \frac{1}{e} \sum_{i=0}^{n} {\varpi}_{M}^{i+n} \sum_{j=0}^{e-1} \zeta^{(i-l)j} = {\varpi}_{M}^{l+n}. \end{align*}$$
So, if for any
![]() $\chi \in \operatorname {\mathrm {Irr}}(H)$
, we choose the unique integer
$\chi \in \operatorname {\mathrm {Irr}}(H)$
, we choose the unique integer
![]() $(\chi ,s)_{H,n}$
in the set
$(\chi ,s)_{H,n}$
in the set
such that
![]() $\chi (s) = \zeta ^{(\chi ,s)_{H,n}}$
, then we see that
$\chi (s) = \zeta ^{(\chi ,s)_{H,n}}$
, then we see that
 $$ \begin{align} \operatorname{\mathrm{Det}}({\mathbf r}_H(\alpha))(\chi) = \sum_{j=0}^{e-1} s^j(\alpha) \zeta^{-(l+n)j} = {\varpi}_{M}^{(\chi,s)_{H,n}}. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Det}}({\mathbf r}_H(\alpha))(\chi) = \sum_{j=0}^{e-1} s^j(\alpha) \zeta^{-(l+n)j} = {\varpi}_{M}^{(\chi,s)_{H,n}}. \end{align} $$
The cases
![]() $n =0$
and
$n =0$
and
![]() $n = (1-e)/2$
(for e odd) correspond to the ring of integers and the square root of the inverse different, respectively, and we see the appearance of the relevant Stickelberger pairing (see Definition 5.1) in each case.
$n = (1-e)/2$
(for e odd) correspond to the ring of integers and the square root of the inverse different, respectively, and we see the appearance of the relevant Stickelberger pairing (see Definition 5.1) in each case.
It follows from (4.2) that
As
![]() $B_n$
is an
$B_n$
is an
![]() $O_L$
-basis of the ideal
$O_L$
-basis of the ideal
![]() ${\varpi }_{M}^{n} \cdot O_{M}$
, and as
${\varpi }_{M}^{n} \cdot O_{M}$
, and as
![]() $\zeta _{e} \in O_L$
, we see that
$\zeta _{e} \in O_L$
, we see that
i.e.,
![]() $\alpha $
is a free generator of
$\alpha $
is a free generator of
![]() ${\varpi }^{n}_{M} \cdot O_M$
as an
${\varpi }^{n}_{M} \cdot O_M$
as an
![]() $O_{L}H$
-module.
$O_{L}H$
-module.
Definition 4.2 If
![]() $g \in G$
, we set
$g \in G$
, we set
 $$\begin{align*}\beta_g := \frac{1}{|g|} \sum_{i=0}^{|g|-1} {\varpi}^{i/|g|}; \end{align*}$$
$$\begin{align*}\beta_g := \frac{1}{|g|} \sum_{i=0}^{|g|-1} {\varpi}^{i/|g|}; \end{align*}$$
note that
![]() $\beta _g$
depends only on
$\beta _g$
depends only on
![]() $|g|$
, and so in particular we have
$|g|$
, and so in particular we have
for every
![]() $\gamma \in G$
. We define
$\gamma \in G$
. We define
![]() ${\varphi }_{g} \in \operatorname {\mathrm {Map}}(G, L^{c})$
by setting
${\varphi }_{g} \in \operatorname {\mathrm {Map}}(G, L^{c})$
by setting
 $$\begin{align*}{\varphi}_{g}(\gamma) = \begin{cases} \sigma^{i}(\beta_g), &\text{if }\gamma = g^i, \\ 0, &\text{if }\gamma \notin \langle g \rangle. \end{cases} \end{align*}$$
$$\begin{align*}{\varphi}_{g}(\gamma) = \begin{cases} \sigma^{i}(\beta_g), &\text{if }\gamma = g^i, \\ 0, &\text{if }\gamma \notin \langle g \rangle. \end{cases} \end{align*}$$
Then
 $$ \begin{align} {\mathbf r}_G({\varphi}_{g}) = \sum_{i=0}^{|g|-1} {\varphi}_{g}(g^i) g^{-i} = \sum_{i=0}^{|g|-1} \sigma^{i}(\beta_g) g^{-i}. \end{align} $$
$$ \begin{align} {\mathbf r}_G({\varphi}_{g}) = \sum_{i=0}^{|g|-1} {\varphi}_{g}(g^i) g^{-i} = \sum_{i=0}^{|g|-1} \sigma^{i}(\beta_g) g^{-i}. \end{align} $$
Suppose now that
![]() $\pi \in Z^1(\Omega _L, G)$
, with
$\pi \in Z^1(\Omega _L, G)$
, with
![]() $[\pi ] \in H^1_t(L,G)$
. Write
$[\pi ] \in H^1_t(L,G)$
. Write
![]() $s:= \pi (\sigma )$
and
$s:= \pi (\sigma )$
and
![]() $t:= \pi (\phi )$
. We define,
$t:= \pi (\phi )$
. We define,
![]() $\pi _{r}, \pi _{nr} \in \operatorname {\mathrm {Map}}(\Omega ^t, G)$
by setting
$\pi _{r}, \pi _{nr} \in \operatorname {\mathrm {Map}}(\Omega ^t, G)$
by setting
so that
It may be shown that in fact
![]() $\pi _{nr} \in \operatorname {\mathrm {Hom}}(\Omega ^{nr}, G)$
, and so corresponds to a unramified G-extension
$\pi _{nr} \in \operatorname {\mathrm {Hom}}(\Omega ^{nr}, G)$
, and so corresponds to a unramified G-extension
![]() $L_{\pi _{nr}}$
of L. It may also be shown that
$L_{\pi _{nr}}$
of L. It may also be shown that
![]() $\pi _{r} |_{\Omega _{r}}\in \operatorname {\mathrm {Hom}}(\Omega ^r, G)$
, corresponding to a totally (tamely) ramified extension
$\pi _{r} |_{\Omega _{r}}\in \operatorname {\mathrm {Hom}}(\Omega ^r, G)$
, corresponding to a totally (tamely) ramified extension
![]() $L^{nr}_{\pi _{r}}/L^{nr}$
. If we write
$L^{nr}_{\pi _{r}}/L^{nr}$
. If we write
![]() $[{\widetilde {\pi }}]$
for the image of
$[{\widetilde {\pi }}]$
for the image of
![]() $[\pi ]$
under the natural restriction map
$[\pi ]$
under the natural restriction map
![]() $H^1(L, G) \to H^1(L^{nr},G)$
, then
$H^1(L, G) \to H^1(L^{nr},G)$
, then
![]() $[{\widetilde {\pi }}] = [\pi _{r}]$
. The element
$[{\widetilde {\pi }}] = [\pi _{r}]$
. The element
![]() ${\varphi }_s$
is a normal integral basis generator of the extension
${\varphi }_s$
is a normal integral basis generator of the extension
![]() $L^{nr}_{\pi _{r}}/L^{nr}$
. (See [Reference Agboola and McCulloh2, Section 7] for proofs of these assertions.) If in addition
$L^{nr}_{\pi _{r}}/L^{nr}$
. (See [Reference Agboola and McCulloh2, Section 7] for proofs of these assertions.) If in addition
![]() $|s|$
is odd, then the inverse different of
$|s|$
is odd, then the inverse different of
![]() $L_{\pi }/L$
has a square root
$L_{\pi }/L$
has a square root
![]() $A_\pi $
, and
$A_\pi $
, and
We can now state the Stickelberger factorization theorem for resolvends of normal integral bases.
Theorem 4.3 If
![]() $a_{nr} \in L_{\pi _{nr}}$
is any normal integral basis generator of
$a_{nr} \in L_{\pi _{nr}}$
is any normal integral basis generator of
![]() $L_{\pi _{nr}}/L$
, then the element
$L_{\pi _{nr}}/L$
, then the element
![]() $a \in L_{\pi }$
defined by
$a \in L_{\pi }$
defined by
is a normal integral basis generator of
![]() $L_{\pi }/L$
.
$L_{\pi }/L$
.
Proof See [Reference Agboola and McCulloh2, Theorem 7.9].
We shall now describe a similar result (due to Tsang when G is abelian) concerning
![]() $O_LG$
-generators of the square root of the inverse different of a tame extension of L.
$O_LG$
-generators of the square root of the inverse different of a tame extension of L.
Definition 4.4 Suppose that
![]() $g \in G$
and that
$g \in G$
and that
![]() $|g|$
is odd. Set
$|g|$
is odd. Set
 $$\begin{align*}\beta^{*}_{g} = \frac{1}{|g|} \sum_{i=0}^{|g|-1} {\varpi}^{\frac{1}{|g|}(i + \frac{1-|g|}{2})}. \end{align*}$$
$$\begin{align*}\beta^{*}_{g} = \frac{1}{|g|} \sum_{i=0}^{|g|-1} {\varpi}^{\frac{1}{|g|}(i + \frac{1-|g|}{2})}. \end{align*}$$
Define
![]() ${\varphi }^{*}_{g} \in \operatorname {\mathrm {Map}}(G, L^{c})$
by
${\varphi }^{*}_{g} \in \operatorname {\mathrm {Map}}(G, L^{c})$
by
 $$\begin{align*}{\varphi}^{*}_{g}(\gamma) = \begin{cases} \sigma^{i}(\beta^{*}_{g}), &\text{if }\gamma = g^i, \\ 0, &\text{if }\gamma \notin \langle g \rangle. \end{cases} \end{align*}$$
$$\begin{align*}{\varphi}^{*}_{g}(\gamma) = \begin{cases} \sigma^{i}(\beta^{*}_{g}), &\text{if }\gamma = g^i, \\ 0, &\text{if }\gamma \notin \langle g \rangle. \end{cases} \end{align*}$$
Then
 $$ \begin{align} {\mathbf r}_G({\varphi}^{*}_{g}) = \sum_{i=0}^{|g|-1} {\varphi}_{g}(g^i) g^{-i} = \sum_{i=0}^{|g|-1} \sigma^{i}(\beta^{*}_{g}) g^{-i}. \end{align} $$
$$ \begin{align} {\mathbf r}_G({\varphi}^{*}_{g}) = \sum_{i=0}^{|g|-1} {\varphi}_{g}(g^i) g^{-i} = \sum_{i=0}^{|g|-1} \sigma^{i}(\beta^{*}_{g}) g^{-i}. \end{align} $$
Theorem 4.5 (Cf. [Reference Agboola and McCulloh2, Theorem 7.9])
If
![]() $a_{nr}$
is any choice of n.i.b. generator of
$a_{nr}$
is any choice of n.i.b. generator of
![]() $L_{\pi _{nr}}/L$
, then the element b of
$L_{\pi _{nr}}/L$
, then the element b of
![]() $L_{\pi }$
defined by
$L_{\pi }$
defined by
satisfies
![]() $A_\pi = O_{L}G \cdot b$
.
$A_\pi = O_{L}G \cdot b$
.
Proof To ease notation, set
![]() $N:= L^{nr}$
and
$N:= L^{nr}$
and
![]() $H := \langle s \rangle $
.
$H := \langle s \rangle $
.
Write
![]() $[{\widetilde {\pi }}] \in H^1(N, G)$
for the image of
$[{\widetilde {\pi }}] \in H^1(N, G)$
for the image of
![]() $[\pi ] \in H^1(L, G)$
under the restriction map
$[\pi ] \in H^1(L, G)$
under the restriction map
![]() $H^1(L, G) \to H^1(N, G)$
. Then
$H^1(L, G) \to H^1(N, G)$
. Then
![]() $A_{{\widetilde {\pi }}} = O_{N}\cdot A_\pi $
because
$A_{{\widetilde {\pi }}} = O_{N}\cdot A_\pi $
because
![]() $N/L$
is unramified. Hence, to establish the desired result, it suffices to show that
$N/L$
is unramified. Hence, to establish the desired result, it suffices to show that
As
![]() ${\mathbf r}_G(a_{nr}) \in (O_{N}G)^{\times }$
, (4.9) is equivalent to the equality
${\mathbf r}_G(a_{nr}) \in (O_{N}G)^{\times }$
, (4.9) is equivalent to the equality
Now,
where
![]() $N^{{\widetilde {\pi }}} = N({\varpi }^{1/|s|})$
(cf. (3.1)), and this isomorphism induces a decomposition
$N^{{\widetilde {\pi }}} = N({\varpi }^{1/|s|})$
(cf. (3.1)), and this isomorphism induces a decomposition
where
is the square root of the inverse different of the extension
![]() $N^{{\widetilde {\pi }}}/N$
.
$N^{{\widetilde {\pi }}}/N$
.
It therefore follows from the definition of
![]() ${\varphi }^{*}_{s}$
that (4.10) holds if and only if
${\varphi }^{*}_{s}$
that (4.10) holds if and only if
This last equality follows exactly as in [Reference Tsang28, Proposition 4.2.2], and a proof is given by taking
![]() $n = (1-e)/2$
(for e odd) in Example 4.1.
$n = (1-e)/2$
(for e odd) in Example 4.1.
Proposition 4.6 Suppose that
![]() $[\pi ] \in H^{1}_{t}(L,G)$
and that
$[\pi ] \in H^{1}_{t}(L,G)$
and that
![]() $s := \pi (\sigma )$
is of odd order. Then the class
$s := \pi (\sigma )$
is of odd order. Then the class
is represented by
![]() $\operatorname {\mathrm {Det}}({\mathbf r}_G({\varphi }^{*}_{s})) \cdot \operatorname {\mathrm {Det}}({\mathbf r}_G({\varphi }_{s}))^{-1} \in \operatorname {\mathrm {Det}}(LG)^{\times }$
.
$\operatorname {\mathrm {Det}}({\mathbf r}_G({\varphi }^{*}_{s})) \cdot \operatorname {\mathrm {Det}}({\mathbf r}_G({\varphi }_{s}))^{-1} \in \operatorname {\mathrm {Det}}(LG)^{\times }$
.
5 Stickelberger pairings and resolvends
Our goal in this section is to describe explicitly the elements
![]() $\operatorname {\mathrm {Det}}({\mathbf r}_G({\varphi }_s))$
and
$\operatorname {\mathrm {Det}}({\mathbf r}_G({\varphi }_s))$
and
![]() $\operatorname {\mathrm {Det}}({\mathbf r}_G({\varphi }^{*}_{s}))$
constructed in the previous section. We begin by recalling the definition of two Stickelberger pairings. The first of these is due to McCulloh, whereas the second is due to Tsang in the case of abelian G. See [Reference Agboola and McCulloh2, Definition 9.1] and [Reference Tsang28, Definition 2.5.1].
$\operatorname {\mathrm {Det}}({\mathbf r}_G({\varphi }^{*}_{s}))$
constructed in the previous section. We begin by recalling the definition of two Stickelberger pairings. The first of these is due to McCulloh, whereas the second is due to Tsang in the case of abelian G. See [Reference Agboola and McCulloh2, Definition 9.1] and [Reference Tsang28, Definition 2.5.1].
Definition 5.1 Let
![]() $\zeta = \zeta _{|G|}$
be a fixed, primitive,
$\zeta = \zeta _{|G|}$
be a fixed, primitive,
![]() $|G|$
th root of unity. Suppose first that G is cyclic. For
$|G|$
th root of unity. Suppose first that G is cyclic. For
![]() $g \in G$
and
$g \in G$
and
![]() $\chi \in \operatorname {\mathrm {Irr}}(G)$
, write
$\chi \in \operatorname {\mathrm {Irr}}(G)$
, write
![]() $\chi (g) = \zeta ^r$
for some integer r.
$\chi (g) = \zeta ^r$
for some integer r.
-
(1) We define
where $$\begin{align*}\langle \chi, g \rangle_G = \{r/|G|\}, \end{align*}$$
$$\begin{align*}\langle \chi, g \rangle_G = \{r/|G|\}, \end{align*}$$
 $ 0 \leq \{r/|G|\} <1$
denotes the fractional part of
$ 0 \leq \{r/|G|\} <1$
denotes the fractional part of
 $r/|G|$
.
$r/|G|$
.
Alternatively (cf. Example 4.1, but note that there we worked with the primitive eth root of unity
 $\zeta _{e}$
, where e is the exponent of G), if we choose r to be the unique integer in the set
$\zeta _{e}$
, where e is the exponent of G), if we choose r to be the unique integer in the set
 $\{l : 0 \leq l \leq |G|-1\}$
such that
$\{l : 0 \leq l \leq |G|-1\}$
such that
 $\chi (g) = \zeta ^r$
, then
$\chi (g) = \zeta ^r$
, then  $$\begin{align*}\langle \chi, g \rangle_G = r/|G|. \end{align*}$$
$$\begin{align*}\langle \chi, g \rangle_G = r/|G|. \end{align*}$$
-
(2) Suppose that
 $|G|$
is odd, and choose
$|G|$
is odd, and choose
 $r \in [(1-|G|)/2, (|G|-1)/2]$
to be the unique integer such that
$r \in [(1-|G|)/2, (|G|-1)/2]$
to be the unique integer such that
 $\chi (g) = \zeta ^r$
. Define
$\chi (g) = \zeta ^r$
. Define  $$\begin{align*}\langle \chi, g \rangle^*_G = r/|G|. \end{align*}$$
$$\begin{align*}\langle \chi, g \rangle^*_G = r/|G|. \end{align*}$$
We extend each of these to pairings
via linearity. Finally, we extend the definitions to arbitrary finite groups G by setting $$\begin{align*}\mathbf{Q} R_G \times \mathbf{Q} G \to \mathbf{Q} \end{align*}$$
and
$$\begin{align*}\mathbf{Q} R_G \times \mathbf{Q} G \to \mathbf{Q} \end{align*}$$
and $$\begin{align*}\langle \chi, s \rangle _G := \langle \chi \mid_{\langle s \rangle}, s \rangle_{\langle s \rangle} \end{align*}$$
where the second definition of course only makes sense when the order
$$\begin{align*}\langle \chi, s \rangle _G := \langle \chi \mid_{\langle s \rangle}, s \rangle_{\langle s \rangle} \end{align*}$$
where the second definition of course only makes sense when the order $$\begin{align*}\langle \chi, s \rangle ^*_G := \langle \chi \mid_{\langle s \rangle}, s \rangle^{*}_{\langle s \rangle}, \end{align*}$$
$$\begin{align*}\langle \chi, s \rangle ^*_G := \langle \chi \mid_{\langle s \rangle}, s \rangle^{*}_{\langle s \rangle}, \end{align*}$$
 $|s|$
of s is odd.
$|s|$
of s is odd.
We shall make use of the following alternative descriptions of the above Stickelberger pairing using the standard inner product on
![]() $R_G$
(see [Reference Agboola and McCulloh2, Proposition 9.2]). For each element
$R_G$
(see [Reference Agboola and McCulloh2, Proposition 9.2]). For each element
![]() $s \in G$
, write
$s \in G$
, write
![]() $\zeta _{|s|} = \zeta _{|G|}^{|G|/|s|}$
, and define a character
$\zeta _{|s|} = \zeta _{|G|}^{|G|/|s|}$
, and define a character
![]() $\xi _s$
of
$\xi _s$
of
![]() $\langle s \rangle $
by
$\langle s \rangle $
by
![]() $\xi _{s}(s^i) = \zeta ^{i}_{|s|}$
. Set
$\xi _{s}(s^i) = \zeta ^{i}_{|s|}$
. Set
 $$\begin{align*}\Xi_s := \frac{1}{|s|} \sum_{j=1}^{|s|-1} j \xi^{j}_{s}. \end{align*}$$
$$\begin{align*}\Xi_s := \frac{1}{|s|} \sum_{j=1}^{|s|-1} j \xi^{j}_{s}. \end{align*}$$
For
![]() $|s|$
odd, we also define
$|s|$
odd, we also define
 $$\begin{align*}\Xi^{*}_{s} := \frac{1}{|s|} \sum_{j=1}^{(|s|-1)/2} j(\xi^{j}_{s} - \xi^{-j}_{s}). \end{align*}$$
$$\begin{align*}\Xi^{*}_{s} := \frac{1}{|s|} \sum_{j=1}^{(|s|-1)/2} j(\xi^{j}_{s} - \xi^{-j}_{s}). \end{align*}$$
Let
![]() $(-,-)_G$
denote the standard inner product on
$(-,-)_G$
denote the standard inner product on
![]() $R_G$
.
$R_G$
.
Proposition 5.2
-
(a) If
 $s \in G$
and
$s \in G$
and
 $\chi \in R_G$
, we have
$\chi \in R_G$
, we have  $$\begin{align*}\langle \chi, s \rangle_G = (\operatorname{\mathrm{Ind}}^{G}_{\langle s \rangle} (\Xi_{s}), \chi)_G. \end{align*}$$
$$\begin{align*}\langle \chi, s \rangle_G = (\operatorname{\mathrm{Ind}}^{G}_{\langle s \rangle} (\Xi_{s}), \chi)_G. \end{align*}$$
-
(b) If furthermore
 $|s|$
is odd, then we have
$|s|$
is odd, then we have  $$\begin{align*}\langle \chi, s \rangle^*_G = (\operatorname{\mathrm{Ind}}^{G}_{\langle s \rangle} (\Xi^{*}_{s}), \chi)_G. \end{align*}$$
$$\begin{align*}\langle \chi, s \rangle^*_G = (\operatorname{\mathrm{Ind}}^{G}_{\langle s \rangle} (\Xi^{*}_{s}), \chi)_G. \end{align*}$$
-
(c) If
 $|s|$
is odd, then
$|s|$
is odd, then  $$\begin{align*}\Xi^{*}_{s} - \Xi_s = -\sum_{j = 1}^{(|s|-1)/2} \xi^{-j}_{s}. \end{align*}$$
$$\begin{align*}\Xi^{*}_{s} - \Xi_s = -\sum_{j = 1}^{(|s|-1)/2} \xi^{-j}_{s}. \end{align*}$$
-
(d) For s odd, write
Then, for each $$\begin{align*}d(s) := -\sum_{j = 1}^{(|s|-1)/2} \xi^{-j}_{s}. \end{align*}$$
$$\begin{align*}d(s) := -\sum_{j = 1}^{(|s|-1)/2} \xi^{-j}_{s}. \end{align*}$$
 $\chi \in R_G$
, we have
$\chi \in R_G$
, we have  $$\begin{align*}\langle \chi, s \rangle^{*}_{G} - \langle \chi, s \rangle_G = (\operatorname{\mathrm{Ind}}^{G}_{\langle s \rangle} (d(s)), \chi)_G. \end{align*}$$
$$\begin{align*}\langle \chi, s \rangle^{*}_{G} - \langle \chi, s \rangle_G = (\operatorname{\mathrm{Ind}}^{G}_{\langle s \rangle} (d(s)), \chi)_G. \end{align*}$$
Proof Part (a) is proved in [Reference Agboola and McCulloh2, Proposition 9.2]. The proof of (b) is the same mutatis mutandis. Part (c) follows directly from the definitions of
![]() $\Xi _s$
and
$\Xi _s$
and
![]() $\Xi ^{*}_{s}$
, and then (d) follows from (a) and (b).
$\Xi ^{*}_{s}$
, and then (d) follows from (a) and (b).
We may use Proposition 5.2 to describe the relationship between the two Stickelberger pairings in Definition 5.1 when
![]() $|s|$
is odd.
$|s|$
is odd.
In the sequel, for any finite group
![]() $\Gamma $
(which will be clear from context), and any natural number k, we write
$\Gamma $
(which will be clear from context), and any natural number k, we write
![]() $\psi _k$
for the kth Adams operator on
$\psi _k$
for the kth Adams operator on
![]() $R_{\Gamma }$
. Thus, if
$R_{\Gamma }$
. Thus, if
![]() $\chi \in R_{\Gamma }$
and
$\chi \in R_{\Gamma }$
and
![]() $\gamma \in \Gamma $
, then one has
$\gamma \in \Gamma $
, then one has
![]() $\psi _k(\chi )(\gamma ) = \chi (\gamma ^k)$
. In particular, we recall that, for all k,
$\psi _k(\chi )(\gamma ) = \chi (\gamma ^k)$
. In particular, we recall that, for all k,
![]() $\psi _{k}$
commutes with the restriction and inflation functors, as well as with the action of
$\psi _{k}$
commutes with the restriction and inflation functors, as well as with the action of
![]() $\Omega _{{\mathbf Q}}$
on
$\Omega _{{\mathbf Q}}$
on
![]() $R_\Gamma $
(see [Reference Erez10, Proposition–Definition 3.5]). If L is a number field or a local field, we also write
$R_\Gamma $
(see [Reference Erez10, Proposition–Definition 3.5]). If L is a number field or a local field, we also write
![]() $\psi _k$
for the homomorphism
$\psi _k$
for the homomorphism
defined by setting
for
![]() $f \in \operatorname {\mathrm {Hom}}(R_{\Gamma }, (L^{c})^{\times })$
and
$f \in \operatorname {\mathrm {Hom}}(R_{\Gamma }, (L^{c})^{\times })$
and
![]() $\chi \in R_{\Gamma }$
.
$\chi \in R_{\Gamma }$
.
Proposition 5.3 Suppose that
![]() $s \in G$
is of odd order, and set
$s \in G$
is of odd order, and set
![]() $H:= \langle s \rangle $
.
$H:= \langle s \rangle $
.
-
(a) If
 $1 \leq j \leq |s|-1$
, then
$1 \leq j \leq |s|-1$
, then  $$ \begin{align*} (\Xi^{*}_{s}, \xi^j )_H &= (\Xi_{s}, \xi^{2j} - \xi^j )_H \\ &= (\Xi_{s}, \psi_2(\xi^{j}) - \xi^j)_H. \end{align*} $$
$$ \begin{align*} (\Xi^{*}_{s}, \xi^j )_H &= (\Xi_{s}, \xi^{2j} - \xi^j )_H \\ &= (\Xi_{s}, \psi_2(\xi^{j}) - \xi^j)_H. \end{align*} $$
-
(b) (Tsang) For each
 $\chi \in R_G$
, we have
$\chi \in R_G$
, we have  $$\begin{align*}\langle \chi, s\rangle^*_G = \langle \psi_2(\chi) - \chi, s \rangle_G. \end{align*}$$
$$\begin{align*}\langle \chi, s\rangle^*_G = \langle \psi_2(\chi) - \chi, s \rangle_G. \end{align*}$$
Proof (a) If
![]() $1 \leq j \leq |s|/2$
, then we have
$1 \leq j \leq |s|/2$
, then we have
whereas if
![]() $|s|/2 \leq j \leq s-1$
, then
$|s|/2 \leq j \leq s-1$
, then
 $$\begin{align*}(\Xi_{s}, \xi_{s}^{2j} - \xi_{s}^{j} )_H = \frac{(2j - |s|) -j}{|s|} = \frac{j - |s|}{|s|}. \end{align*}$$
$$\begin{align*}(\Xi_{s}, \xi_{s}^{2j} - \xi_{s}^{j} )_H = \frac{(2j - |s|) -j}{|s|} = \frac{j - |s|}{|s|}. \end{align*}$$
Thus, in each case, we have
and this establishes the claim.
(b) Proposition 5.2(b), together with Frobenius reciprocity, gives
 $$ \begin{align*} \langle \chi, s \rangle^*_G &= (\operatorname{\mathrm{Ind}}^{G}_{\langle s \rangle} (\Xi^{*}_{s}), \chi)_G \\ &= (\Xi^{*}_{s}, \chi \mid_H)_H. \end{align*} $$
$$ \begin{align*} \langle \chi, s \rangle^*_G &= (\operatorname{\mathrm{Ind}}^{G}_{\langle s \rangle} (\Xi^{*}_{s}), \chi)_G \\ &= (\Xi^{*}_{s}, \chi \mid_H)_H. \end{align*} $$
The desired result now follows from part (a), together with the fact that, for any
![]() $\chi \in R_G$
, we have the equality
$\chi \in R_G$
, we have the equality
Remark 5.4 Proposition 5.3(b) (due to Tsang) shows very clearly why the second Adams operator
![]() $\psi _2$
appears when one studies the Galois structure of the square root of the inverse different as opposed to the ring of integers. This appearance of the second Adams operator was first observed by Erez (see [Reference Erez10, Proposition–Definition 3.5 and Theorem 3.6]) in the initial work on this topic.
$\psi _2$
appears when one studies the Galois structure of the square root of the inverse different as opposed to the ring of integers. This appearance of the second Adams operator was first observed by Erez (see [Reference Erez10, Proposition–Definition 3.5 and Theorem 3.6]) in the initial work on this topic.
The following result describes the elements
![]() $\operatorname {\mathrm {Det}}({\mathbf r}_G({\varphi }_{s}))$
and
$\operatorname {\mathrm {Det}}({\mathbf r}_G({\varphi }_{s}))$
and
![]() $\operatorname {\mathrm {Det}}({\mathbf r}_G({\varphi }^{*}_{s}))$
in terms of Stickelberger pairings. In what follows, we retain the notation and conventions of Section 4.
$\operatorname {\mathrm {Det}}({\mathbf r}_G({\varphi }^{*}_{s}))$
in terms of Stickelberger pairings. In what follows, we retain the notation and conventions of Section 4.
Proposition 5.5 Suppose that
![]() $\chi \in R_G$
and
$\chi \in R_G$
and
![]() $s \in G$
.
$s \in G$
.
-
(a) We have
 $$\begin{align*}\operatorname{\mathrm{Det}}({\mathbf r}_G({\varphi}_{s}))(\chi) = {\varpi}^{\langle \chi, s \rangle_G}. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Det}}({\mathbf r}_G({\varphi}_{s}))(\chi) = {\varpi}^{\langle \chi, s \rangle_G}. \end{align*}$$
-
(b) If
 $|s|$
is odd, then we have
$|s|$
is odd, then we have  $$\begin{align*}\operatorname{\mathrm{Det}}({\mathbf r}_G({\varphi}^{*}_{s}))(\chi) = {\varpi}^{\langle \chi, s \rangle^{*}_{G}}. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Det}}({\mathbf r}_G({\varphi}^{*}_{s}))(\chi) = {\varpi}^{\langle \chi, s \rangle^{*}_{G}}. \end{align*}$$
-
(c) For
 $|s|$
odd, we have That is to say,
$|s|$
odd, we have That is to say, $$ \begin{align*} [\operatorname{\mathrm{Det}}({\mathbf r}_G({\varphi}^{*}_{s})) \cdot \operatorname{\mathrm{Det}}({\mathbf r}_G({\varphi}_s))^{-1}] (\chi) &= {\varpi}^{\langle \chi, s \rangle^{*}_{G} -\langle \chi, s \rangle_{G}}\\ &={\varpi}^{\langle \psi_{2}(\chi) - 2\chi, s \rangle_{G}}\\ &= \frac{\operatorname{\mathrm{Det}}({\mathbf r}_G({\varphi}_{s}))(\psi_2(\chi))}{\operatorname{\mathrm{Det}}({\mathbf r}_G({\varphi}_{s}))(2\chi)}. \end{align*} $$
$$ \begin{align*} [\operatorname{\mathrm{Det}}({\mathbf r}_G({\varphi}^{*}_{s})) \cdot \operatorname{\mathrm{Det}}({\mathbf r}_G({\varphi}_s))^{-1}] (\chi) &= {\varpi}^{\langle \chi, s \rangle^{*}_{G} -\langle \chi, s \rangle_{G}}\\ &={\varpi}^{\langle \psi_{2}(\chi) - 2\chi, s \rangle_{G}}\\ &= \frac{\operatorname{\mathrm{Det}}({\mathbf r}_G({\varphi}_{s}))(\psi_2(\chi))}{\operatorname{\mathrm{Det}}({\mathbf r}_G({\varphi}_{s}))(2\chi)}. \end{align*} $$
 $$\begin{align*}\operatorname{\mathrm{Det}}({\mathbf r}_G({\varphi}^{*}_{s})) \cdot \operatorname{\mathrm{Det}}({\mathbf r}_G({\varphi}_s))^{-1} = \psi_2(\operatorname{\mathrm{Det}}({\mathbf r}_G({\varphi}_{s}))) \cdot \operatorname{\mathrm{Det}}({\mathbf r}_G({\varphi}_{s}))^{-2}. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Det}}({\mathbf r}_G({\varphi}^{*}_{s})) \cdot \operatorname{\mathrm{Det}}({\mathbf r}_G({\varphi}_s))^{-1} = \psi_2(\operatorname{\mathrm{Det}}({\mathbf r}_G({\varphi}_{s}))) \cdot \operatorname{\mathrm{Det}}({\mathbf r}_G({\varphi}_{s}))^{-2}. \end{align*}$$
Proof Part (a) is proved in [Reference Agboola and McCulloh2, Proposition 10.5(a)]. The proof of (b) is very similar, using [Reference Tsang28, Proposition 4.2.2], which in fact shows the result for G abelian. Part (c) follows from parts (a) and (b), and Proposition 5.3.
Corollary 5.6 Suppose that
![]() $[\pi ] \in H^1_t(L,G)$
and that
$[\pi ] \in H^1_t(L,G)$
and that
![]() $s:= \pi (\sigma )$
is of odd order. Then a representing homomorphism for the class
$s:= \pi (\sigma )$
is of odd order. Then a representing homomorphism for the class
in
 $$\begin{align*}K_0(O_LG, L) \simeq \frac{\operatorname{\mathrm{Det}}(LG)^{\times}}{\operatorname{\mathrm{Det}}(O_LG)^{\times}} \simeq \frac{\operatorname{\mathrm{Hom}}_{\Omega_{L}}(R_G, (L^{c})^{\times})}{\operatorname{\mathrm{Det}}(O_LG)^{\times}} \end{align*}$$
$$\begin{align*}K_0(O_LG, L) \simeq \frac{\operatorname{\mathrm{Det}}(LG)^{\times}}{\operatorname{\mathrm{Det}}(O_LG)^{\times}} \simeq \frac{\operatorname{\mathrm{Hom}}_{\Omega_{L}}(R_G, (L^{c})^{\times})}{\operatorname{\mathrm{Det}}(O_LG)^{\times}} \end{align*}$$
is the map
![]() $f_{\pi } \in \operatorname {\mathrm {Hom}}_{\Omega _{L}}(R_G, (L^{c})^{\times })$
given by
$f_{\pi } \in \operatorname {\mathrm {Hom}}_{\Omega _{L}}(R_G, (L^{c})^{\times })$
given by
6 Galois–Gauss and Galois–Jacobi sums
Let L be a local field of residual characteristic p. Suppose that
![]() $[\pi ] \in H^1_t(L, G)$
, and recall that we have (see (3.1))
$[\pi ] \in H^1_t(L, G)$
, and recall that we have (see (3.1))
Set
![]() $H := \pi (\Omega _L) = \operatorname {\mathrm {Gal}}(L^{\pi }/L)$
, and write
$H := \pi (\Omega _L) = \operatorname {\mathrm {Gal}}(L^{\pi }/L)$
, and write
![]() $\tau ^{*}(L^{\pi }/L,\, -) \in \operatorname {\mathrm {Hom}}(R_{H}, ({\mathbf Q}^c)^{\times })$
for the adjusted Galois–Gauss sum homomorphism associated with
$\tau ^{*}(L^{\pi }/L,\, -) \in \operatorname {\mathrm {Hom}}(R_{H}, ({\mathbf Q}^c)^{\times })$
for the adjusted Galois–Gauss sum homomorphism associated with
![]() $L^{\pi }/L$
(see [Reference Fröhlich14, Chapter IV, equation (1.7)]). Recall that this is defined by
$L^{\pi }/L$
(see [Reference Fröhlich14, Chapter IV, equation (1.7)]). Recall that this is defined by
where
![]() $\tau (L^{\pi }/L,\, -)$
denotes the Galois–Gauss sum homomorphism and
$\tau (L^{\pi }/L,\, -)$
denotes the Galois–Gauss sum homomorphism and
![]() $y(L^{\pi }/L, -)$
and
$y(L^{\pi }/L, -)$
and
![]() $z(L^{\pi }/L, -)$
are homomorphisms taking values in roots of unity in
$z(L^{\pi }/L, -)$
are homomorphisms taking values in roots of unity in
![]() ${\mathbf Q}^c$
. We define
${\mathbf Q}^c$
. We define
![]() $\tau ^{*}(L_{\pi }/L,\, -) \in \operatorname {\mathrm {Hom}}(R_{G}, ({\mathbf Q}^c)^{\times })$
by composing
$\tau ^{*}(L_{\pi }/L,\, -) \in \operatorname {\mathrm {Hom}}(R_{G}, ({\mathbf Q}^c)^{\times })$
by composing
![]() $\tau ^{*}(L^{\pi }/L,\, -)$
with the natural map
$\tau ^{*}(L^{\pi }/L,\, -)$
with the natural map
![]() $R_G \to R_H$
.
$R_G \to R_H$
.
For a finite group
![]() $\Gamma $
, we write
$\Gamma $
, we write
![]() $\operatorname {\mathrm {Irr}}_p(\Gamma )$
for the set of
$\operatorname {\mathrm {Irr}}_p(\Gamma )$
for the set of
![]() ${\mathbf Q}_{p}^{c}$
-valued irreducible characters of
${\mathbf Q}_{p}^{c}$
-valued irreducible characters of
![]() $\Gamma $
and
$\Gamma $
and
![]() $R_{\Gamma , p}$
for the free abelian group on
$R_{\Gamma , p}$
for the free abelian group on
![]() $\operatorname {\mathrm {Irr}}_p(\Gamma )$
. We fix a local embedding
$\operatorname {\mathrm {Irr}}_p(\Gamma )$
. We fix a local embedding
![]() $\operatorname {\mathrm {Loc}}_p: {\mathbf Q}^c \to {\mathbf Q}^c_p$
, and we shall identify
$\operatorname {\mathrm {Loc}}_p: {\mathbf Q}^c \to {\mathbf Q}^c_p$
, and we shall identify
![]() $\operatorname {\mathrm {Irr}}(\Gamma )$
with
$\operatorname {\mathrm {Irr}}(\Gamma )$
with
![]() $\operatorname {\mathrm {Irr}}_p(\Gamma )$
via this choice of embedding.
$\operatorname {\mathrm {Irr}}_p(\Gamma )$
via this choice of embedding.
For each rational prime
![]() $l \neq p$
, we fix a semilocal embedding
$l \neq p$
, we fix a semilocal embedding
![]() $\operatorname {\mathrm {Loc}}_l: {\mathbf Q}^c \to ({\mathbf Q}^c)_l := {\mathbf Q}^c \otimes _{{\mathbf Q}} {\mathbf Q}_{l}$
. (Caveat: note that this is not the same thing as a local embedding
$\operatorname {\mathrm {Loc}}_l: {\mathbf Q}^c \to ({\mathbf Q}^c)_l := {\mathbf Q}^c \otimes _{{\mathbf Q}} {\mathbf Q}_{l}$
. (Caveat: note that this is not the same thing as a local embedding
![]() ${\mathbf Q}^c \to {\mathbf Q}^c_l$
!) For each rational prime l, write
${\mathbf Q}^c \to {\mathbf Q}^c_l$
!) For each rational prime l, write
![]() ${\mathbf Q}^t_l$
for the maximal, tamely ramified extension of
${\mathbf Q}^t_l$
for the maximal, tamely ramified extension of
![]() ${\mathbf Q}_l$
.
${\mathbf Q}_l$
.
We shall require the following results. (We remind the reader that the definition of the Adams operators
![]() $\psi _k$
was recalled just prior to the statement of Proposition 5.3.)
$\psi _k$
was recalled just prior to the statement of Proposition 5.3.)
Proposition 6.1 Fix a rational prime l.
-
(a) Let K be an unramified extension of
 ${\mathbf Q}_{l}$
. Then, for any integer k, we have that
${\mathbf Q}_{l}$
. Then, for any integer k, we have that  $$\begin{align*}\psi_k(\operatorname{\mathrm{Det}}(O_{K}G)^{\times}) \subseteq \operatorname{\mathrm{Det}}(O_{K}G)^{\times}. \end{align*}$$
$$\begin{align*}\psi_k(\operatorname{\mathrm{Det}}(O_{K}G)^{\times}) \subseteq \operatorname{\mathrm{Det}}(O_{K}G)^{\times}. \end{align*}$$
-
(b) Let
 $\Gamma $
be a finite group with abelian p-Sylow subgroups. Then, for any integer k,
$\Gamma $
be a finite group with abelian p-Sylow subgroups. Then, for any integer k,  $$\begin{align*}\psi_k(\operatorname{\mathrm{Det}}(O_{{\mathbf Q}_{p}^{t}} \Gamma)^{\times}) \subseteq \operatorname{\mathrm{Det}}(O_{{\mathbf Q}_{p}^{t}} \Gamma)^{\times}. \end{align*}$$
$$\begin{align*}\psi_k(\operatorname{\mathrm{Det}}(O_{{\mathbf Q}_{p}^{t}} \Gamma)^{\times}) \subseteq \operatorname{\mathrm{Det}}(O_{{\mathbf Q}_{p}^{t}} \Gamma)^{\times}. \end{align*}$$
-
(c) Suppose that
 $l \neq p$
. Then
$l \neq p$
. Then  $$\begin{align*}\operatorname{\mathrm{Loc}}_l(\tau^{*}(L_{\pi}/L,\, -)) \in \operatorname{\mathrm{Det}}(O_{{\mathbf Q}(\mu_p),l} G)^{\times}. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Loc}}_l(\tau^{*}(L_{\pi}/L,\, -)) \in \operatorname{\mathrm{Det}}(O_{{\mathbf Q}(\mu_p),l} G)^{\times}. \end{align*}$$
Proof Parts (a) and (b) are results of Cassou–Noguès and Taylor. For part (a), see, e.g., [Reference Taylor27, Chapter 9, Theorem 1.2], and note that for this particular result, we do not need to assume that
![]() $(k, |G|) = 1$
. For part (b), see [Reference Cassou-Nogues, Taylor, Halter-Koch and Tichy5, p. 83, Remark].
$(k, |G|) = 1$
. For part (b), see [Reference Cassou-Nogues, Taylor, Halter-Koch and Tichy5, p. 83, Remark].
Part (c) follows from [Reference Fröhlich14, Chapter IV, Theorem 30], where analogous results are proved for
![]() $\tau ^{*}(L^{\pi }/L,\,-)$
; the corresponding results for
$\tau ^{*}(L^{\pi }/L,\,-)$
; the corresponding results for
![]() $\tau ^{*}(L_{\pi }/L,\,-)$
are then a direct consequence of the definition of
$\tau ^{*}(L_{\pi }/L,\,-)$
are then a direct consequence of the definition of
![]() $\tau ^{*}(L_{\pi }/L,\,-)$
.
$\tau ^{*}(L_{\pi }/L,\,-)$
.
The following result is entirely analogous to [Reference Fröhlich14, Chapter IV, Lemma 2.1]. Recall that if
![]() $f \in \operatorname {\mathrm {Hom}}(R_{\Gamma }, ({\mathbf Q}^{c}_{p})^{\times })$
, then
$f \in \operatorname {\mathrm {Hom}}(R_{\Gamma }, ({\mathbf Q}^{c}_{p})^{\times })$
, then
![]() $\omega \in \Omega _{{\mathbf Q}_{p}}$
acts on f by the rule
$\omega \in \Omega _{{\mathbf Q}_{p}}$
acts on f by the rule
Lemma 6.2 Let
![]() $L/{\mathbf Q}_p$
be a finite extension, and let
$L/{\mathbf Q}_p$
be a finite extension, and let
![]() $\{\nu \}$
be any right transversal of
$\{\nu \}$
be any right transversal of
![]() $\Omega _L$
in
$\Omega _L$
in
![]() $\Omega _{{\mathbf Q}_{p}}$
. Suppose that
$\Omega _{{\mathbf Q}_{p}}$
. Suppose that
![]() $f \in \operatorname {\mathrm {Hom}}_{\Omega _{L^{\operatorname {\mathrm {nr}}}}}(R_{\Gamma }, ({\mathbf Q}_{p}^{c})^{\times })$
. Then (cf. (2.5) and (2.6)):
$f \in \operatorname {\mathrm {Hom}}_{\Omega _{L^{\operatorname {\mathrm {nr}}}}}(R_{\Gamma }, ({\mathbf Q}_{p}^{c})^{\times })$
. Then (cf. (2.5) and (2.6)):
Proof It suffices to show that this result holds with respect to a particular choice of transversal of
![]() $\Omega _L$
in
$\Omega _L$
in
![]() $\Omega _{{\mathbf Q}_{p}}$
.
$\Omega _{{\mathbf Q}_{p}}$
.
We first observe that, as
![]() $\Omega _{{\mathbf Q}^{\operatorname {\mathrm {nr}}}_{p}}$
is normal in
$\Omega _{{\mathbf Q}^{\operatorname {\mathrm {nr}}}_{p}}$
is normal in
![]() $\Omega _{{\mathbf Q}_{p}}$
,
$\Omega _{{\mathbf Q}_{p}}$
,
![]() $\Omega _L \cdot \Omega _{{\mathbf Q}^{\operatorname {\mathrm {nr}}}_{p}}$
is a subgroup of
$\Omega _L \cdot \Omega _{{\mathbf Q}^{\operatorname {\mathrm {nr}}}_{p}}$
is a subgroup of
![]() $\Omega _{{\mathbf Q}_{p}}$
. We choose a right transversal
$\Omega _{{\mathbf Q}_{p}}$
. We choose a right transversal
![]() $\{\omega \}$
of
$\{\omega \}$
of
![]() $\Omega _L \cdot \Omega _{{\mathbf Q}^{\operatorname {\mathrm {nr}}}_{p}}$
in
$\Omega _L \cdot \Omega _{{\mathbf Q}^{\operatorname {\mathrm {nr}}}_{p}}$
in
![]() $\Omega _{{\mathbf Q}_{p}}$
.
$\Omega _{{\mathbf Q}_{p}}$
.
Next, we choose a right transversal
![]() $\{\sigma \}$
of
$\{\sigma \}$
of
![]() $\Omega _L \cap \Omega _{{\mathbf Q}^{\operatorname {\mathrm {nr}}}_{p}}$
in
$\Omega _L \cap \Omega _{{\mathbf Q}^{\operatorname {\mathrm {nr}}}_{p}}$
in
![]() $\Omega _{{\mathbf Q}^{\operatorname {\mathrm {nr}}}_{p}}$
. It follows that
$\Omega _{{\mathbf Q}^{\operatorname {\mathrm {nr}}}_{p}}$
. It follows that
![]() $\{\sigma \}$
is also a right transversal of
$\{\sigma \}$
is also a right transversal of
![]() $\Omega _L$
in
$\Omega _L$
in
![]() $\Omega _L \cdot \Omega _{{\mathbf Q}^{\operatorname {\mathrm {nr}}}_{p}}$
. We now deduce that
$\Omega _L \cdot \Omega _{{\mathbf Q}^{\operatorname {\mathrm {nr}}}_{p}}$
. We now deduce that
![]() $\{\sigma \omega \}$
is a right transversal of
$\{\sigma \omega \}$
is a right transversal of
![]() $\Omega _L$
in
$\Omega _L$
in
![]() $\Omega _{{\mathbf Q}_{p}}$
. We also note that
$\Omega _{{\mathbf Q}_{p}}$
. We also note that
and that (since
![]() $\Omega _{{\mathbf Q}^{\operatorname {\mathrm {nr}}}_{p}}$
is normal in
$\Omega _{{\mathbf Q}^{\operatorname {\mathrm {nr}}}_{p}}$
is normal in
![]() $\Omega _{{\mathbf Q}_{p}}$
)
$\Omega _{{\mathbf Q}_{p}}$
)
for any
![]() $\omega _i \in \{\omega \}$
.
$\omega _i \in \{\omega \}$
.
Now, suppose that
![]() $f \in \operatorname {\mathrm {Hom}}_{\Omega _{L^{\operatorname {\mathrm {nr}}}}}(R_{\Gamma }, ({\mathbf Q}_{p}^{c})^{\times })$
and that
$f \in \operatorname {\mathrm {Hom}}_{\Omega _{L^{\operatorname {\mathrm {nr}}}}}(R_{\Gamma }, ({\mathbf Q}_{p}^{c})^{\times })$
and that
![]() $\omega _i \in \{\omega \}$
. Then
$\omega _i \in \{\omega \}$
. Then
and so
Now, observe that for fixed
![]() $\omega _i \in \{\omega \}$
,
$\omega _i \in \{\omega \}$
,
![]() $\{\omega ^{-1}_{i} \sigma \omega _i\}_{\sigma }$
is a right transversal of
$\{\omega ^{-1}_{i} \sigma \omega _i\}_{\sigma }$
is a right transversal of
![]() $\omega ^{-1}_{i}\Omega _{L^{\operatorname {\mathrm {nr}}}} \omega _i \cap \Omega _{{\mathbf Q}^{nr}_{p}}$
in
$\omega ^{-1}_{i}\Omega _{L^{\operatorname {\mathrm {nr}}}} \omega _i \cap \Omega _{{\mathbf Q}^{nr}_{p}}$
in
![]() $\Omega _{{\mathbf Q}^{\operatorname {\mathrm {nr}}}_{p}}$
, and so
$\Omega _{{\mathbf Q}^{\operatorname {\mathrm {nr}}}_{p}}$
, and so
Hence, finally, we obtain
as required.
Proposition 6.3 Let
![]() $a_{\pi }$
be any n.i.b. generator of
$a_{\pi }$
be any n.i.b. generator of
![]() $L_{\pi }/L$
. Suppose also that the square root
$L_{\pi }/L$
. Suppose also that the square root
![]() $A_\pi $
of the inverse different of
$A_\pi $
of the inverse different of
![]() $L_{\pi }/L$
exists (i.e., that
$L_{\pi }/L$
exists (i.e., that
![]() $s := \pi (\sigma )$
is of odd order) and that
$s := \pi (\sigma )$
is of odd order) and that
![]() $A_\pi = O_L G \cdot b_{\pi }$
. Then:
$A_\pi = O_L G \cdot b_{\pi }$
. Then:
-
(a)
 $ {\mathcal N}_{L/{\mathbf Q}_{p}}[ \operatorname {\mathrm {Det}}({\mathbf r}_G(b_{\pi }))^{-1} \cdot \psi _2(\operatorname {\mathrm {Det}}({\mathbf r}_G(a_{\pi }))) \cdot \operatorname {\mathrm {Det}}({\mathbf r}_G(a_{\pi }))^{-1}] \in \operatorname {\mathrm {Det}}(O_{{\mathbf Q}^{t}_{p}}G)^{\times }. $
$ {\mathcal N}_{L/{\mathbf Q}_{p}}[ \operatorname {\mathrm {Det}}({\mathbf r}_G(b_{\pi }))^{-1} \cdot \psi _2(\operatorname {\mathrm {Det}}({\mathbf r}_G(a_{\pi }))) \cdot \operatorname {\mathrm {Det}}({\mathbf r}_G(a_{\pi }))^{-1}] \in \operatorname {\mathrm {Det}}(O_{{\mathbf Q}^{t}_{p}}G)^{\times }. $
-
(b)
-
(i)
 $\operatorname {\mathrm {Loc}}_p[(\tau ^{*}(L_{\pi }/L,\, -))]^{-1} \cdot {\mathcal N}_{L/{\mathbf Q}_{p}}[\operatorname {\mathrm {Det}}({\mathbf r}_{G}(a_{\pi })) ] \in \operatorname {\mathrm {Det}}(O_{{\mathbf Q}^{t}_{p}} G)^{\times }$
.
$\operatorname {\mathrm {Loc}}_p[(\tau ^{*}(L_{\pi }/L,\, -))]^{-1} \cdot {\mathcal N}_{L/{\mathbf Q}_{p}}[\operatorname {\mathrm {Det}}({\mathbf r}_{G}(a_{\pi })) ] \in \operatorname {\mathrm {Det}}(O_{{\mathbf Q}^{t}_{p}} G)^{\times }$
. -
(ii)
 $\operatorname {\mathrm {Loc}}_p[\psi _2(\tau ^{*}(L_{\pi }/L,\,-))]^{-1} \cdot {\mathcal N}_{L/{\mathbf Q}_{p}}[\psi _2(\operatorname {\mathrm {Det}}({\mathbf r}_{G}(a_{\pi })))]\in \operatorname {\mathrm {Det}}(O_{{\mathbf Q}^{t}_{p}} G)^{\times }$
.
$\operatorname {\mathrm {Loc}}_p[\psi _2(\tau ^{*}(L_{\pi }/L,\,-))]^{-1} \cdot {\mathcal N}_{L/{\mathbf Q}_{p}}[\psi _2(\operatorname {\mathrm {Det}}({\mathbf r}_{G}(a_{\pi })))]\in \operatorname {\mathrm {Det}}(O_{{\mathbf Q}^{t}_{p}} G)^{\times }$
.
-
-
(c)
 $\operatorname {\mathrm {Loc}}_p[\psi _2(\tau ^{*}(L_{\pi }/L,\, -)) \cdot (\tau ^{*}(L_{\pi }/L,\, -))^{-1}]^{-1} \cdot {\mathcal N}_{L/{\mathbf Q}_p}[\operatorname {\mathrm {Det}}({\mathbf r}_{G}(b_{\pi }))] \in \operatorname {\mathrm {Det}}(O_{{\mathbf Q}^{t}_{p}} G)^{\times }.$
$\operatorname {\mathrm {Loc}}_p[\psi _2(\tau ^{*}(L_{\pi }/L,\, -)) \cdot (\tau ^{*}(L_{\pi }/L,\, -))^{-1}]^{-1} \cdot {\mathcal N}_{L/{\mathbf Q}_p}[\operatorname {\mathrm {Det}}({\mathbf r}_{G}(b_{\pi }))] \in \operatorname {\mathrm {Det}}(O_{{\mathbf Q}^{t}_{p}} G)^{\times }.$
-
(d)
 $ \operatorname {\mathrm {Loc}}_p[\psi _2(\tau ^{*}(L_{\pi }/L,\,-)) \cdot (\tau ^{*}(L_{\pi }/L,\, -))^{-2}]^{-1} \cdot {\mathcal N}_{L/{\mathbf Q}_p}[\operatorname {\mathrm {Det}}({\mathbf r}_{G}(b_{\pi })) \cdot \operatorname {\mathrm {Det}}({\mathbf r}_{G}(a_{\pi }))^{-1}] $
belongs to
$ \operatorname {\mathrm {Loc}}_p[\psi _2(\tau ^{*}(L_{\pi }/L,\,-)) \cdot (\tau ^{*}(L_{\pi }/L,\, -))^{-2}]^{-1} \cdot {\mathcal N}_{L/{\mathbf Q}_p}[\operatorname {\mathrm {Det}}({\mathbf r}_{G}(b_{\pi })) \cdot \operatorname {\mathrm {Det}}({\mathbf r}_{G}(a_{\pi }))^{-1}] $
belongs to
 $\operatorname {\mathrm {Det}}(O_{{\mathbf Q}^{t}_{p}} G)^{\times }$
.
$\operatorname {\mathrm {Det}}(O_{{\mathbf Q}^{t}_{p}} G)^{\times }$
. -
(e) With the notation of Proposition 4.6, the element
 $$\begin{align*}\operatorname{\mathrm{Loc}}_p[\psi_2(\tau^{*}(L_{\pi}/L,\,-)) \cdot (\tau^{*}(L_{\pi}/L,\, -))^{-2}]^{-1} \cdot {\mathcal N}_{L/{\mathbf Q}_p}[\operatorname{\mathrm{Det}}({\mathbf r}_{G}({\varphi}^{*}_{s})) \cdot \operatorname{\mathrm{Det}}({\mathbf r}_{G}({\varphi}_{s}))^{-1}] \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Loc}}_p[\psi_2(\tau^{*}(L_{\pi}/L,\,-)) \cdot (\tau^{*}(L_{\pi}/L,\, -))^{-2}]^{-1} \cdot {\mathcal N}_{L/{\mathbf Q}_p}[\operatorname{\mathrm{Det}}({\mathbf r}_{G}({\varphi}^{*}_{s})) \cdot \operatorname{\mathrm{Det}}({\mathbf r}_{G}({\varphi}_{s}))^{-1}] \end{align*}$$
belongs to
 $\operatorname {\mathrm {Det}}(O_{{\mathbf Q}^{t}_{p}} G)^{\times }$
.
$\operatorname {\mathrm {Det}}(O_{{\mathbf Q}^{t}_{p}} G)^{\times }$
.
Proof (a) Recall from [Reference Agboola and McCulloh2, Definition 7.12] that for any n.i.b. generator
![]() $a_{\pi }$
of
$a_{\pi }$
of
![]() $L_{\pi }/L$
, one has
$L_{\pi }/L$
, one has
where
![]() $u \in (O_LG)^{\times }$
and
$u \in (O_LG)^{\times }$
and
![]() ${\mathbf r}_{G}(a_{nr})\in (O_{L^{nr}}G)^{\times }$
. Furthermore,
${\mathbf r}_{G}(a_{nr})\in (O_{L^{nr}}G)^{\times }$
. Furthermore,
![]() $u\cdot a_{nr}$
is also an n.i.b generator of
$u\cdot a_{nr}$
is also an n.i.b generator of
![]() $L_{\pi _{nr}}/L$
.
$L_{\pi _{nr}}/L$
.
Hence,
and Lemma 6.2 implies that also
It now follows from Proposition 6.1 that the product
belongs to
![]() $\operatorname {\mathrm {Det}}(O_{{\mathbf Q}_{p}^{nr}}G)^\times $
.
$\operatorname {\mathrm {Det}}(O_{{\mathbf Q}_{p}^{nr}}G)^\times $
.
Part (a) now follows from (6.1), together with Proposition 5.5(c) and the Stickelberger factorization of
![]() ${\mathbf r}_G(b_{\pi })$
(see Theorem 4.5).
${\mathbf r}_G(b_{\pi })$
(see Theorem 4.5).
(b) Let
![]() $O^\pi $
denote the integral closure of
$O^\pi $
denote the integral closure of
![]() $O_L$
in
$O_L$
in
![]() $L^\pi $
and fix an element
$L^\pi $
and fix an element
![]() $\alpha \in L^{\pi }$
such that
$\alpha \in L^{\pi }$
such that
![]() $O^{\pi } = O_LH \cdot \alpha $
. It follows from [Reference Fröhlich14, Chapter IV, Theorem 31] that there exists an element
$O^{\pi } = O_LH \cdot \alpha $
. It follows from [Reference Fröhlich14, Chapter IV, Theorem 31] that there exists an element
![]() $w\in (O_{{\mathbf Q}_{p}^{t}}H)^\times $
such that
$w\in (O_{{\mathbf Q}_{p}^{t}}H)^\times $
such that
Under our hypotheses, the inertia subgroup of H is cyclic of order
![]() $|s|$
coprime to p. Hence, Proposition 6.1(b) implies that
$|s|$
coprime to p. Hence, Proposition 6.1(b) implies that
belongs to
![]() $\psi _{2}(\operatorname {\mathrm {Det}}(O_{{\mathbf Q}_{p}^{t}}H)^\times ) \subseteq \operatorname {\mathrm {Det}}(O_{{\mathbf Q}_{p}^{t}}H)^\times \subseteq \operatorname {\mathrm {Det}}(O_{{\mathbf Q}_{p}^{t}}G)^\times $
.
$\psi _{2}(\operatorname {\mathrm {Det}}(O_{{\mathbf Q}_{p}^{t}}H)^\times ) \subseteq \operatorname {\mathrm {Det}}(O_{{\mathbf Q}_{p}^{t}}H)^\times \subseteq \operatorname {\mathrm {Det}}(O_{{\mathbf Q}_{p}^{t}}G)^\times $
.
Next, we construct a map
![]() $a_{\pi } \in \mathrm {Map}(G, L^c)$
associated with
$a_{\pi } \in \mathrm {Map}(G, L^c)$
associated with
![]() $\alpha $
by setting
$\alpha $
by setting
 $$\begin{align*}a_{\pi}(\gamma) := \left\{ \begin{array}{ll} \tilde{\gamma}(\alpha), & \quad \mbox{if } \quad \gamma=\pi(\tilde{\gamma}) \text{ for } \tilde{\gamma} \in \Omega_{L}, \\ 0, & \quad \mbox{otherwise}.\end{array} \right. \end{align*}$$
$$\begin{align*}a_{\pi}(\gamma) := \left\{ \begin{array}{ll} \tilde{\gamma}(\alpha), & \quad \mbox{if } \quad \gamma=\pi(\tilde{\gamma}) \text{ for } \tilde{\gamma} \in \Omega_{L}, \\ 0, & \quad \mbox{otherwise}.\end{array} \right. \end{align*}$$
It is easy to see from (3.1) that
![]() $a_{\pi } \in L_\pi $
and satisfies that
$a_{\pi } \in L_\pi $
and satisfies that
![]() $O_{\pi } = O_LG \cdot a$
. In particular, for each
$O_{\pi } = O_LG \cdot a$
. In particular, for each
![]() $\chi \in R_{G}$
, we have
$\chi \in R_{G}$
, we have
with
![]() $\mathrm {res}:= \mathrm {res}^{G}_H: R_+{G} \to R_{H}$
. This implies that
$\mathrm {res}:= \mathrm {res}^{G}_H: R_+{G} \to R_{H}$
. This implies that
 $$ \begin{align} \begin{array}{rl} {\mathcal N}_{L/{\mathbf Q}_{p}}[\operatorname{\mathrm{Det}}({\mathbf r}_{G}(a_{\pi}))] =\, & {\mathcal N}_{L/{\mathbf Q}_{p}}[\operatorname{\mathrm{Det}}({\mathbf r}_{H}(\alpha))] ,\\ {\mathcal N}_{L/{\mathbf Q}_{p}}[\psi_2(\operatorname{\mathrm{Det}}({\mathbf r}_{G}(a_{\pi})))] =\, & {\mathcal N}_{L/{\mathbf Q}_{p}}[\psi_2(\operatorname{\mathrm{Det}}({\mathbf r}_{H}(\alpha)))] .\\ \end{array} \end{align} $$
$$ \begin{align} \begin{array}{rl} {\mathcal N}_{L/{\mathbf Q}_{p}}[\operatorname{\mathrm{Det}}({\mathbf r}_{G}(a_{\pi}))] =\, & {\mathcal N}_{L/{\mathbf Q}_{p}}[\operatorname{\mathrm{Det}}({\mathbf r}_{H}(\alpha))] ,\\ {\mathcal N}_{L/{\mathbf Q}_{p}}[\psi_2(\operatorname{\mathrm{Det}}({\mathbf r}_{G}(a_{\pi})))] =\, & {\mathcal N}_{L/{\mathbf Q}_{p}}[\psi_2(\operatorname{\mathrm{Det}}({\mathbf r}_{H}(\alpha)))] .\\ \end{array} \end{align} $$
We now see from the definition of
![]() $\tau ^{\ast }(L_{\pi }/L, - )$
that (i) follows from (6.2) and (6.4), whereas part (ii) is a consequence of (6.3) and (6.4).
$\tau ^{\ast }(L_{\pi }/L, - )$
that (i) follows from (6.2) and (6.4), whereas part (ii) is a consequence of (6.3) and (6.4).
(c) Follows from (a) and (b) above.
(d) Follows from (b)(i) together with (c).
(e) Follows from (d) above.
Proposition 6.3(d) and (e) motivates the following definition.
Definition 6.4 We retain the notation established above. Define the adjusted Galois–Jacobi sum homomorphism associated with
![]() $L_{\pi }/L$
,
$L_{\pi }/L$
,
![]() $J^*(L_{\pi }/L,\,-) \in \operatorname {\mathrm {Hom}}(R_{G}, ({\mathbf Q}^c)^{\times })$
, by
$J^*(L_{\pi }/L,\,-) \in \operatorname {\mathrm {Hom}}(R_{G}, ({\mathbf Q}^c)^{\times })$
, by
It follows from the Galois action formulae for Galois–Gauss sums (see [Reference Fröhlich14, pp. 119 and 152]) that in fact
![]() $J^*(L_{\pi }/L,\,-) \in \operatorname {\mathrm {Hom}}_{\Omega _{{\mathbf Q}}}(R_{\Gamma }, ({\mathbf Q}^c)^{\times })$
.
$J^*(L_{\pi }/L,\,-) \in \operatorname {\mathrm {Hom}}_{\Omega _{{\mathbf Q}}}(R_{\Gamma }, ({\mathbf Q}^c)^{\times })$
.
Remark 6.5 Let
![]() $\tau (L^{\pi }/L,\,-) \in \operatorname {\mathrm {Hom}}(R_{H}, ({\mathbf Q}^{c})^{\times })$
denote the (unadjusted) Galois–Gauss sum associated with
$\tau (L^{\pi }/L,\,-) \in \operatorname {\mathrm {Hom}}(R_{H}, ({\mathbf Q}^{c})^{\times })$
denote the (unadjusted) Galois–Gauss sum associated with
![]() $L^{\pi }/L$
, and write
$L^{\pi }/L$
, and write
![]() $\tau (L_{\pi }/L,\,-) \in \operatorname {\mathrm {Hom}}(R_{G}, ({\mathbf Q}^{c})^{\times })$
for the composition of
$\tau (L_{\pi }/L,\,-) \in \operatorname {\mathrm {Hom}}(R_{G}, ({\mathbf Q}^{c})^{\times })$
for the composition of
![]() $\tau (L^{\pi }/L,\,-)$
with the natural map
$\tau (L^{\pi }/L,\,-)$
with the natural map
![]() $R_G \to R_H$
. We remark that the Galois–Jacobi sum
$R_G \to R_H$
. We remark that the Galois–Jacobi sum
![]() $J(L_{\pi }/L,\, -) \in \operatorname {\mathrm {Hom}}(R_{G}, ({\mathbf Q}^c)^{\times })$
defined by
$J(L_{\pi }/L,\, -) \in \operatorname {\mathrm {Hom}}(R_{G}, ({\mathbf Q}^c)^{\times })$
defined by
is a special case of the non-abelian Jacobi sums first introduced by Fröhlich (see [Reference Fröhlich13]).
Proposition 6.6
-
(a) Suppose that
 $l \neq p$
. Then
$l \neq p$
. Then  $$\begin{align*}\operatorname{\mathrm{Loc}}_l(J^*(L_{\pi}/L, -)) \in \operatorname{\mathrm{Det}}({\mathbf Z}_l G^{\times}). \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Loc}}_l(J^*(L_{\pi}/L, -)) \in \operatorname{\mathrm{Det}}({\mathbf Z}_l G^{\times}). \end{align*}$$
-
(b) Using the notation of Proposition 6.3, we have
Hence, $$\begin{align*}\operatorname{\mathrm{Loc}}_p(J^*(L_{\pi}/L,\, -))^{-1} \cdot {\mathcal N}_{L/{\mathbf Q}_p}[\operatorname{\mathrm{Det}}({\mathbf r}_{G}(b_{\pi})) \cdot \operatorname{\mathrm{Det}}({\mathbf r}_{G}(a_{\pi}))^{-1}] \in \operatorname{\mathrm{Det}}({\mathbf Z}_p G^{\times}). \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Loc}}_p(J^*(L_{\pi}/L,\, -))^{-1} \cdot {\mathcal N}_{L/{\mathbf Q}_p}[\operatorname{\mathrm{Det}}({\mathbf r}_{G}(b_{\pi})) \cdot \operatorname{\mathrm{Det}}({\mathbf r}_{G}(a_{\pi}))^{-1}] \in \operatorname{\mathrm{Det}}({\mathbf Z}_p G^{\times}). \end{align*}$$
 $$\begin{align*}\operatorname{\mathrm{Loc}}_p(J^*(L_{\pi}/L,\, -))^{-1} \cdot {\mathcal N}_{L/{\mathbf Q}_p}[\operatorname{\mathrm{Det}}({\mathbf r}_{G}({\varphi}^{*}_{s})) \cdot \operatorname{\mathrm{Det}}({\mathbf r}_{G}({\varphi}_s))^{-1}] \in \operatorname{\mathrm{Det}}({\mathbf Z}_p G^{\times}). \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Loc}}_p(J^*(L_{\pi}/L,\, -))^{-1} \cdot {\mathcal N}_{L/{\mathbf Q}_p}[\operatorname{\mathrm{Det}}({\mathbf r}_{G}({\varphi}^{*}_{s})) \cdot \operatorname{\mathrm{Det}}({\mathbf r}_{G}({\varphi}_s))^{-1}] \in \operatorname{\mathrm{Det}}({\mathbf Z}_p G^{\times}). \end{align*}$$
Proof (a) Recall that
![]() $J^*(L_{\pi }/L,\, -) \in \operatorname {\mathrm {Hom}}_{\Omega _{{\mathbf Q}}}(R_{G}, ({\mathbf Q}^c)^{\times })$
and that
$J^*(L_{\pi }/L,\, -) \in \operatorname {\mathrm {Hom}}_{\Omega _{{\mathbf Q}}}(R_{G}, ({\mathbf Q}^c)^{\times })$
and that
![]() ${\mathbf Q}(\mu _p)/{\mathbf Q}$
is unramified at l. It therefore follows from Proposition 6.1(a) and (c), together with Taylor’s fixed point theorem for determinants (see [Reference Taylor27, Chapter 8, Theorem 1.2]), that
${\mathbf Q}(\mu _p)/{\mathbf Q}$
is unramified at l. It therefore follows from Proposition 6.1(a) and (c), together with Taylor’s fixed point theorem for determinants (see [Reference Taylor27, Chapter 8, Theorem 1.2]), that
as claimed.
(b) As both of the functions
![]() $\operatorname {\mathrm {Loc}}_p(J^*(L_{\pi }/L,\,-))$
and
$\operatorname {\mathrm {Loc}}_p(J^*(L_{\pi }/L,\,-))$
and
![]() ${\mathcal N}_{L/{\mathbf Q}_p}[\operatorname {\mathrm {Det}}({\mathbf r}_{G}(b_{\pi })) \cdot \operatorname {\mathrm {Det}}({\mathbf r}_{G}(a_{\pi }))^{-1}]$
lie in
${\mathcal N}_{L/{\mathbf Q}_p}[\operatorname {\mathrm {Det}}({\mathbf r}_{G}(b_{\pi })) \cdot \operatorname {\mathrm {Det}}({\mathbf r}_{G}(a_{\pi }))^{-1}]$
lie in
![]() $\operatorname {\mathrm {Hom}}_{\Omega _{{\mathbf Q}_{p}}}(R_{G}, ({\mathbf Q}^{c}_{p})^{\times })$
, we see from Proposition 6.3(d) that
$\operatorname {\mathrm {Hom}}_{\Omega _{{\mathbf Q}_{p}}}(R_{G}, ({\mathbf Q}^{c}_{p})^{\times })$
, we see from Proposition 6.3(d) that
 $$\begin{align*}&\operatorname{\mathrm{Loc}}_p(J^*(L_{\pi}/L,\, -))^{-1} \cdot {\mathcal N}_{L/{\mathbf Q}_p}[\operatorname{\mathrm{Det}}({\mathbf r}_{G}(b_{\pi})) \cdot \operatorname{\mathrm{Det}}({\mathbf r}_{G}(a_{\pi}))^{-1}] \\&\quad\in [\operatorname{\mathrm{Det}}(O_{{\mathbf Q}^{t}_{p}} G^{\times})]^{\Omega_{{\mathbf Q}_{p}}} = \operatorname{\mathrm{Det}}({\mathbf Z}_p G^{\times}). \end{align*}$$
$$\begin{align*}&\operatorname{\mathrm{Loc}}_p(J^*(L_{\pi}/L,\, -))^{-1} \cdot {\mathcal N}_{L/{\mathbf Q}_p}[\operatorname{\mathrm{Det}}({\mathbf r}_{G}(b_{\pi})) \cdot \operatorname{\mathrm{Det}}({\mathbf r}_{G}(a_{\pi}))^{-1}] \\&\quad\in [\operatorname{\mathrm{Det}}(O_{{\mathbf Q}^{t}_{p}} G^{\times})]^{\Omega_{{\mathbf Q}_{p}}} = \operatorname{\mathrm{Det}}({\mathbf Z}_p G^{\times}). \end{align*}$$
The final assertion now follows at once from the Stickelberger factorizations of
![]() ${\mathbf r}_G(a_\pi )$
and
${\mathbf r}_G(a_\pi )$
and
![]() ${\mathbf r}_G(b_\pi )$
(see Theorems 4.3 and 4.5).
${\mathbf r}_G(b_\pi )$
(see Theorems 4.3 and 4.5).
7 Symplectic Galois–Jacobi sums I
In this section, we fix data
![]() $L, G$
, and
$L, G$
, and
![]() $\pi $
as in Section 6. We write
$\pi $
as in Section 6. We write
![]() $\mathrm {Symp}(G)$
for the set of irreducible symplectic characters of G. For each
$\mathrm {Symp}(G)$
for the set of irreducible symplectic characters of G. For each
![]() $\chi \in \operatorname {\mathrm {Irr}}(G)$
, we write
$\chi \in \operatorname {\mathrm {Irr}}(G)$
, we write
![]() $\tau (L_\pi /L, \chi )$
for the associated (unadjusted) Galois–Gauss sum, and
$\tau (L_\pi /L, \chi )$
for the associated (unadjusted) Galois–Gauss sum, and
for the (unadjusted) Galois–Jacobi sum (see Remark 6.5).
We shall prove the following result concerning symplectic Galois–Jacobi sums.
Theorem 7.1 Suppose that
![]() $\chi \in \operatorname {\mathrm {Symp}}(G)$
. Then
$\chi \in \operatorname {\mathrm {Symp}}(G)$
. Then
![]() $J(L_\pi /L, \chi )$
is a strictly positive real number.
$J(L_\pi /L, \chi )$
is a strictly positive real number.
We see from the decomposition (3.1) that it is enough to prove this result after replacing the Galois algebra
![]() $L_\pi $
by the field
$L_\pi $
by the field
![]() $L^{\pi }$
and the group G by the Galois group
$L^{\pi }$
and the group G by the Galois group
![]() $\pi (\Omega _L) = \operatorname {\mathrm {Gal}}(L^{\pi }/L)$
. In the sequel, we shall therefore restrict to the case where
$\pi (\Omega _L) = \operatorname {\mathrm {Gal}}(L^{\pi }/L)$
. In the sequel, we shall therefore restrict to the case where
![]() $L_\pi /L$
is a finite Galois extension of p-adic fields and G is its Galois group.
$L_\pi /L$
is a finite Galois extension of p-adic fields and G is its Galois group.
To prove Theorem 7.1, it is therefore enough to show that for each
![]() $\chi $
in
$\chi $
in
![]() $\mathrm {Symp}(G)$
, the quotient
$\mathrm {Symp}(G)$
, the quotient
![]() $\tau (L, \psi _{2}(\chi ))/\tau (L, 2\chi )$
is a strictly positive real number.
$\tau (L, \psi _{2}(\chi ))/\tau (L, 2\chi )$
is a strictly positive real number.
To verify this, we recall that since each such
![]() $\chi $
is real-valued, the definition of the local root number
$\chi $
is real-valued, the definition of the local root number
![]() $W(L,\chi )$
implies that
$W(L,\chi )$
implies that
(cf. [Reference Martinet and Fröhlich18, Chapter II, Section 4, Definition]). Hence, since
![]() $\mathbf {N}_{L}\mathfrak {f}(L_\pi /L, \chi )^{1/2}>0$
, it is enough to prove the following result.
$\mathbf {N}_{L}\mathfrak {f}(L_\pi /L, \chi )^{1/2}>0$
, it is enough to prove the following result.
Theorem 7.2 Let
![]() $E/F$
be a tamely ramified Galois extension of non-archimedean local fields that has odd ramification degree and set
$E/F$
be a tamely ramified Galois extension of non-archimedean local fields that has odd ramification degree and set
![]() $G := \operatorname {\mathrm {Gal}}(E/F)$
. Then, for each
$G := \operatorname {\mathrm {Gal}}(E/F)$
. Then, for each
![]() $\chi $
in
$\chi $
in
![]() $\mathrm {Symp}(G)$
, one has
$\mathrm {Symp}(G)$
, one has
![]() $W(F,\psi _2(\chi )) = W(F,2\chi ) = 1$
.
$W(F,\psi _2(\chi )) = W(F,2\chi ) = 1$
.
This sort of result is, in principle, hard to prove both because root numbers of symplectic characters are difficult to compute and because Adams operators do not in general commute with induction functors. We therefore prove two preliminary results that help address these problems.
The first of these results is entirely representation-theoretic in nature.
In the sequel, for any finite group
![]() $\Gamma $
and character
$\Gamma $
and character
![]() $\phi $
in
$\phi $
in
![]() $R_\Gamma $
, we write
$R_\Gamma $
, we write
![]() $\mathrm {Tr}(\phi )$
for the real-valued character
$\mathrm {Tr}(\phi )$
for the real-valued character
![]() $\phi + \overline {\phi }$
.
$\phi + \overline {\phi }$
.
Lemma 7.3 Let
![]() $\Delta $
be a subgroup of a finite group
$\Delta $
be a subgroup of a finite group
![]() $\Gamma $
, fix a character
$\Gamma $
, fix a character
![]() $\phi $
of
$\phi $
of
![]() $\Delta $
, and consider the virtual character
$\Delta $
, and consider the virtual character
For elements
![]() $\gamma $
and
$\gamma $
and
![]() $\delta $
of
$\delta $
of
![]() $\Gamma $
, we set
$\Gamma $
, we set
![]() $\gamma ^\delta := \delta \gamma \delta ^{-1}$
.
$\gamma ^\delta := \delta \gamma \delta ^{-1}$
.
-
(a) Let
 $\mathcal {T}$
be a set of coset representatives of
$\mathcal {T}$
be a set of coset representatives of
 $\Delta $
in
$\Delta $
in
 $\Gamma $
. Then, for every
$\Gamma $
. Then, for every
 $\gamma \in \Gamma $
, one has where the sum runs over all
$\gamma \in \Gamma $
, one has where the sum runs over all $$ \begin{align*} (\mathrm{I}_{\Gamma}^2(\phi))(\gamma) = \sum_{\tau}\phi((\gamma^\tau)^2), \end{align*} $$
$$ \begin{align*} (\mathrm{I}_{\Gamma}^2(\phi))(\gamma) = \sum_{\tau}\phi((\gamma^\tau)^2), \end{align*} $$
 $\tau \in \mathcal {T}$
for which
$\tau \in \mathcal {T}$
for which
 $(\gamma ^\tau )^2 \in \Delta $
and
$(\gamma ^\tau )^2 \in \Delta $
and
 $\gamma ^\tau \notin \Delta $
.
$\gamma ^\tau \notin \Delta $
.
-
(b) If
 $\Delta $
is a subnormal subgroup of
$\Delta $
is a subnormal subgroup of
 $\Gamma $
of odd index, then
$\Gamma $
of odd index, then
 $\mathrm {I}_{\Gamma }^2(\phi ) = 0$
.
$\mathrm {I}_{\Gamma }^2(\phi ) = 0$
. -
(c) Assume that
 $\Gamma $
is a semidirect product of a supersolvable group by an abelian normal subgroup
$\Gamma $
is a semidirect product of a supersolvable group by an abelian normal subgroup
 $\Upsilon $
.
$\Upsilon $
.-
(i) Then, for every irreducible character
 $\mu $
of
$\mu $
of
 $\Gamma $
, there exists a subgroup
$\Gamma $
, there exists a subgroup
 $\Upsilon '$
of
$\Upsilon '$
of
 $\Gamma $
that contains
$\Gamma $
that contains
 $\Upsilon $
and a linear character
$\Upsilon $
and a linear character
 $\lambda $
of
$\lambda $
of
 $\Upsilon '$
such that
$\Upsilon '$
such that
 $\mu = \mathrm { Ind}_{\Upsilon '}^\Gamma (\lambda )$
.
$\mu = \mathrm { Ind}_{\Upsilon '}^\Gamma (\lambda )$
.
In addition, if
 $\Upsilon \subseteq \Delta $
, the index of
$\Upsilon \subseteq \Delta $
, the index of
 $\Delta $
in
$\Delta $
in
 $\Gamma $
is a power of
$\Gamma $
is a power of
 $2$
and
$2$
and
 $\Gamma $
has cyclic Sylow
$\Gamma $
has cyclic Sylow
 $2$
-subgroups, then the following claims are also valid.
$2$
-subgroups, then the following claims are also valid.-
(ii) If
 $\phi $
is real-valued, then
$\phi $
is real-valued, then
 $\mathrm {I}_{\Gamma }^2(\phi )$
is an integral linear combination of characters of the form
$\mathrm {I}_{\Gamma }^2(\phi )$
is an integral linear combination of characters of the form
 $\mathrm {Ind}_{\Delta '}^\Gamma \lambda $
and
$\mathrm {Ind}_{\Delta '}^\Gamma \lambda $
and
 $\mathrm {Tr}(\phi ')$
, where
$\mathrm {Tr}(\phi ')$
, where
 $\Delta '$
runs over subgroups of
$\Delta '$
runs over subgroups of
 $\Gamma $
that contain
$\Gamma $
that contain
 $\Delta $
,
$\Delta $
,
 $\lambda $
over homomorphisms
$\lambda $
over homomorphisms
 $\Delta ' \to \{\pm 1\}$
and
$\Delta ' \to \{\pm 1\}$
and
 $\phi '$
over elements of
$\phi '$
over elements of
 $R_\Gamma $
.
$R_\Gamma $
. -
(iii) If
 $\phi $
is induced from a proper normal subgroup of
$\phi $
is induced from a proper normal subgroup of
 $\Delta $
of
$\Delta $
of
 $2$
-power index that contains
$2$
-power index that contains
 $\Upsilon $
, then
$\Upsilon $
, then
 $\mathrm {I}_{\Gamma }^2(\phi )=0$
.
$\mathrm {I}_{\Gamma }^2(\phi )=0$
.
-
-
(d) Assume that
 $\Gamma $
is generalized quaternion,
$\Gamma $
is generalized quaternion,
 $\Delta $
is the cyclic subgroup of
$\Delta $
is the cyclic subgroup of
 $\Gamma $
of index
$\Gamma $
of index
 $2$
, and
$2$
, and
 $\phi $
is irreducible (and hence linear). Then
$\phi $
is irreducible (and hence linear). Then
 $\phi ^2$
is trivial on the center Z of
$\phi ^2$
is trivial on the center Z of
 $\Gamma $
and where we regard
$\Gamma $
and where we regard $$\begin{align*}\psi_2\bigl(\mathrm{Ind}_\Delta^\Gamma\phi\bigr) = \mathrm{Inf}_{\Gamma/Z}^\Gamma\bigl(\mathrm{Ind}_{\Delta/Z}^{\Gamma/Z}(\phi^2)\bigr) + \mathrm{Inf}_{\Gamma/\Delta}^\Gamma(\chi_{\Gamma/\Delta}) - \mathbf{1}_\Gamma,\end{align*}$$
$$\begin{align*}\psi_2\bigl(\mathrm{Ind}_\Delta^\Gamma\phi\bigr) = \mathrm{Inf}_{\Gamma/Z}^\Gamma\bigl(\mathrm{Ind}_{\Delta/Z}^{\Gamma/Z}(\phi^2)\bigr) + \mathrm{Inf}_{\Gamma/\Delta}^\Gamma(\chi_{\Gamma/\Delta}) - \mathbf{1}_\Gamma,\end{align*}$$
 $\phi ^2$
as a character of
$\phi ^2$
as a character of
 $\Delta /Z$
and write
$\Delta /Z$
and write
 $\chi _{\Gamma /\Delta }$
for the unique nontrivial homomorphism
$\chi _{\Gamma /\Delta }$
for the unique nontrivial homomorphism
 $\Gamma /\Delta \to ({\mathbf Q}^{c})^{\times }$
.
$\Gamma /\Delta \to ({\mathbf Q}^{c})^{\times }$
.
Proof Part (a) follows directly from the explicit formula for induced characters and the fact that for each
![]() $\gamma \in \Gamma $
, and
$\gamma \in \Gamma $
, and
![]() $\tau \in \mathcal {T}$
, one has
$\tau \in \mathcal {T}$
, one has
![]() $(\gamma ^\tau )^2\in \Delta $
whenever
$(\gamma ^\tau )^2\in \Delta $
whenever
![]() $\gamma ^\tau \in \Delta $
.
$\gamma ^\tau \in \Delta $
.
To prove part (b), we fix a chain of subgroups
such that each
![]() $\Gamma (i)$
is normal in
$\Gamma (i)$
is normal in
![]() $\Gamma (i+1)$
. Then the equality
$\Gamma (i+1)$
. Then the equality
 $$ \begin{align} \mathrm{I}^2_\Gamma(\phi) = \sum_{i=1}^{i = t-1} \mathrm{Ind}_{\Gamma(i+1)}^\Gamma \bigl( \mathrm{I}_{\Gamma(i+1), \Gamma(i)}^2(\mathrm{Ind}^{\Gamma(i)}_\Delta\phi) \bigr), \end{align} $$
$$ \begin{align} \mathrm{I}^2_\Gamma(\phi) = \sum_{i=1}^{i = t-1} \mathrm{Ind}_{\Gamma(i+1)}^\Gamma \bigl( \mathrm{I}_{\Gamma(i+1), \Gamma(i)}^2(\mathrm{Ind}^{\Gamma(i)}_\Delta\phi) \bigr), \end{align} $$
where
reduces us to the case
![]() $\Delta $
is normal in
$\Delta $
is normal in
![]() $\Gamma $
. In this case, the claim follows immediately from the formula in part (a) and the fact that under the stated conditions, for every
$\Gamma $
. In this case, the claim follows immediately from the formula in part (a) and the fact that under the stated conditions, for every
![]() $\gamma \in \Gamma $
and
$\gamma \in \Gamma $
and
![]() $\tau \in \mathcal {T}$
, one has
$\tau \in \mathcal {T}$
, one has
![]() $(\gamma ^\tau )^2 \in \Delta \Longleftrightarrow \gamma ^\tau \in \Delta $
.
$(\gamma ^\tau )^2 \in \Delta \Longleftrightarrow \gamma ^\tau \in \Delta $
.
Turning to part (c), we note first that under the stated hypothesis on
![]() $\Gamma $
, claim (c)(i) follows from [Reference Serre22, Section 8.5, Exercise 8.10] and the argument of [Reference Serre22, Section 8.2, Proposition 25].
$\Gamma $
, claim (c)(i) follows from [Reference Serre22, Section 8.5, Exercise 8.10] and the argument of [Reference Serre22, Section 8.2, Proposition 25].
To verify (c)(ii) and (c)(iii), we assume the additional hypotheses on
![]() $\Gamma $
and note, in particular, that since
$\Gamma $
and note, in particular, that since
![]() $\Gamma $
has cyclic Sylow
$\Gamma $
has cyclic Sylow
![]() $2$
-subgroups, Cayley’s normal
$2$
-subgroups, Cayley’s normal
![]() $2$
-complement theorem implies that
$2$
-complement theorem implies that
![]() $\Gamma $
, and therefore also its quotient
$\Gamma $
, and therefore also its quotient
![]() $\Gamma /\Upsilon $
, has a normal
$\Gamma /\Upsilon $
, has a normal
![]() $2$
-complement. Writing
$2$
-complement. Writing
![]() $\Upsilon _1/\Upsilon $
for the normal
$\Upsilon _1/\Upsilon $
for the normal
![]() $2$
-complement of
$2$
-complement of
![]() $\Gamma /\Upsilon $
, the given assumptions imply
$\Gamma /\Upsilon $
, the given assumptions imply
![]() $\Upsilon _1\subseteq \Delta $
and so, since
$\Upsilon _1\subseteq \Delta $
and so, since
![]() $\Gamma /\Upsilon _1$
is cyclic of
$\Gamma /\Upsilon _1$
is cyclic of
![]() $2$
-power order, there exists a chain of subgroups (7.1) in which
$2$
-power order, there exists a chain of subgroups (7.1) in which
![]() $\Gamma (i)$
has index
$\Gamma (i)$
has index
![]() $2$
in
$2$
in
![]() $\Gamma (i+1)$
for each i. The corresponding equality (7.2) then reduces claims (c)(ii) and (c)(iii) to the case that
$\Gamma (i+1)$
for each i. The corresponding equality (7.2) then reduces claims (c)(ii) and (c)(iii) to the case that
![]() $\Delta $
has index 2 in
$\Delta $
has index 2 in
![]() $\Gamma $
. In this case,
$\Gamma $
. In this case,
![]() $|\mathcal {T}| = 2$
and, for every
$|\mathcal {T}| = 2$
and, for every
![]() $\gamma \in \Gamma $
and
$\gamma \in \Gamma $
and
![]() $\tau \in \mathcal {T}$
, one has
$\tau \in \mathcal {T}$
, one has
![]() $(\gamma ^\tau )^2\in \Delta $
and, in addition,
$(\gamma ^\tau )^2\in \Delta $
and, in addition,
![]() $\gamma ^\tau \notin \Delta \Longleftrightarrow \gamma \notin \Delta $
and so the formula in part (a) implies
$\gamma ^\tau \notin \Delta \Longleftrightarrow \gamma \notin \Delta $
and so the formula in part (a) implies
 $$ \begin{align} (I_\Gamma^2(\phi))(\gamma) = \begin{cases} 0, &\text{ if }\gamma\in \Delta,\\ \sum_{\tau\in \mathcal{T}}\phi((\gamma^\tau)^2), &\text{ if }\gamma\notin \Delta.\end{cases}\end{align} $$
$$ \begin{align} (I_\Gamma^2(\phi))(\gamma) = \begin{cases} 0, &\text{ if }\gamma\in \Delta,\\ \sum_{\tau\in \mathcal{T}}\phi((\gamma^\tau)^2), &\text{ if }\gamma\notin \Delta.\end{cases}\end{align} $$
Now, by (c)(i), every irreducible character of
![]() $\Gamma $
has the form
$\Gamma $
has the form
![]() $\mu = \mathrm {Ind}_{\Upsilon '}^\Gamma (\lambda )$
, where
$\mu = \mathrm {Ind}_{\Upsilon '}^\Gamma (\lambda )$
, where
![]() $\Upsilon '$
is a suitable subgroup of
$\Upsilon '$
is a suitable subgroup of
![]() $\Gamma $
that contains
$\Gamma $
that contains
![]() $\Upsilon $
and
$\Upsilon $
and
![]() $\lambda $
a linear character of
$\lambda $
a linear character of
![]() $\Upsilon '$
. Furthermore, if
$\Upsilon '$
. Furthermore, if
![]() $\Upsilon '\not \subset \Delta $
, then the index of
$\Upsilon '\not \subset \Delta $
, then the index of
![]() $\Upsilon '$
in
$\Upsilon '$
in
![]() $\Gamma $
is odd, so
$\Gamma $
is odd, so
![]() $\mu $
has odd degree and so, by [Reference Navarro, Sanus and Tiep20, Theorem A], is real-valued if and only if it is a homomorphism of the form
$\mu $
has odd degree and so, by [Reference Navarro, Sanus and Tiep20, Theorem A], is real-valued if and only if it is a homomorphism of the form
![]() $\Upsilon ' \to \{\pm 1\}$
. Claim (c)(ii) follows directly from this fact and the observation that
$\Upsilon ' \to \{\pm 1\}$
. Claim (c)(ii) follows directly from this fact and the observation that
![]() $I_\Gamma ^2(\phi )$
is real-valued if
$I_\Gamma ^2(\phi )$
is real-valued if
![]() $\phi $
is real-valued.
$\phi $
is real-valued.
To prove claim (c)(iii), we assume that
![]() $\phi = \mathrm {Ind}_{\Delta '}^\Delta \phi '$
, where
$\phi = \mathrm {Ind}_{\Delta '}^\Delta \phi '$
, where
![]() $\Delta '$
is a normal subgroup of
$\Delta '$
is a normal subgroup of
![]() $\Delta $
that contains
$\Delta $
that contains
![]() $\Upsilon $
and is of
$\Upsilon $
and is of
![]() $2$
-power index. In this case, the formula (7.3) implies that if
$2$
-power index. In this case, the formula (7.3) implies that if
![]() $I_\Gamma ^2(\phi )$
is nonzero, then there exists an element of
$I_\Gamma ^2(\phi )$
is nonzero, then there exists an element of
![]() $\Gamma \setminus \Delta $
whose square belongs to
$\Gamma \setminus \Delta $
whose square belongs to
![]() $\Delta '$
. However, since
$\Delta '$
. However, since
![]() $\Upsilon _1 \subseteq \Delta '$
, the image in the (cyclic) group
$\Upsilon _1 \subseteq \Delta '$
, the image in the (cyclic) group
![]() $\Gamma /\Delta '$
of any element in
$\Gamma /\Delta '$
of any element in
![]() $\Gamma \setminus \Delta $
has order divisible by
$\Gamma \setminus \Delta $
has order divisible by
![]() $4$
and so its square cannot belong to
$4$
and so its square cannot belong to
![]() $\Delta '$
. This proves (c)(iii).
$\Delta '$
. This proves (c)(iii).
Next, under the hypotheses of (d), for every
![]() $\gamma \in \Gamma $
, one has
$\gamma \in \Gamma $
, one has
![]() $\gamma ^2 \in \Delta $
and hence
$\gamma ^2 \in \Delta $
and hence
In particular, since
![]() $\phi ^2(z) = 1$
for every
$\phi ^2(z) = 1$
for every
![]() $z\in Z$
, this formula implies that
$z\in Z$
, this formula implies that
![]() $\psi _2(\mathrm {Ind}_\Delta ^\Gamma \phi )$
is the inflation of a character function on the dihedral group
$\psi _2(\mathrm {Ind}_\Delta ^\Gamma \phi )$
is the inflation of a character function on the dihedral group
![]() $\Gamma /Z$
, and then the displayed formula in part (d) is verified by an easy explicit computation.
$\Gamma /Z$
, and then the displayed formula in part (d) is verified by an easy explicit computation.
In the sequel, for each finite Galois extension
![]() $E/F$
of p-adic fields, and each complex character
$E/F$
of p-adic fields, and each complex character
![]() $\chi $
of
$\chi $
of
![]() $\operatorname {\mathrm {Gal}}(E/F)$
, we abbreviate the root number
$\operatorname {\mathrm {Gal}}(E/F)$
, we abbreviate the root number
![]() $W(F,\chi )$
to
$W(F,\chi )$
to
![]() $W(\chi )$
.
$W(\chi )$
.
Part (c) of the following result relies on the central result of Fröhlich and Queyrut in [Reference Fröhlich and Queyrut16].
Proposition 7.4 Let
![]() $E/F$
be a finite Galois extension of p-adic fields. Set
$E/F$
be a finite Galois extension of p-adic fields. Set
![]() $G := \operatorname {\mathrm {Gal}}(E/F)$
and assume that the inertia subgroup of G has odd order.
$G := \operatorname {\mathrm {Gal}}(E/F)$
and assume that the inertia subgroup of G has odd order.
-
(a) For all
 $\phi $
in
$\phi $
in
 $R_G$
, one has
$R_G$
, one has
 $W(\mathrm {Tr}(\phi )) = 1$
.
$W(\mathrm {Tr}(\phi )) = 1$
. -
(b) If H is a normal subgroup of G and
 $G/H$
is cyclic, then for each
$G/H$
is cyclic, then for each
 $\phi $
in
$\phi $
in
 $R_H$
, one has where, in the second case,
$R_H$
, one has where, in the second case, $$\begin{align*}W(\mathrm{Ind}_H^G\phi) = \begin{cases} W(\phi), &\text{if }G/H\text{ has odd order,}\\ W(\phi)W(\chi_{G/H})^{\phi(1)}, &\text{if }G/H\text{ has even order,}\end{cases}\end{align*}$$
$$\begin{align*}W(\mathrm{Ind}_H^G\phi) = \begin{cases} W(\phi), &\text{if }G/H\text{ has odd order,}\\ W(\phi)W(\chi_{G/H})^{\phi(1)}, &\text{if }G/H\text{ has even order,}\end{cases}\end{align*}$$
 $\chi _{E'/F}$
is the nontrivial character of
$\chi _{E'/F}$
is the nontrivial character of
 $\operatorname {\mathrm {Gal}}(E'/F)$
, with
$\operatorname {\mathrm {Gal}}(E'/F)$
, with
 $E'$
the quadratic extension of F in E.
$E'$
the quadratic extension of F in E.
-
(c) Assume that G is dihedral of order congruent to
 $2$
modulo
$2$
modulo
 $4$
, write L for the unique quadratic extension of F in E, and set
$4$
, write L for the unique quadratic extension of F in E, and set
 $H := \operatorname {\mathrm {Gal}}(E/L)$
. Then, for each homomorphism
$H := \operatorname {\mathrm {Gal}}(E/L)$
. Then, for each homomorphism
 $\phi : H\to ({\mathbf Q}^{c})^{\times }$
, one has
$\phi : H\to ({\mathbf Q}^{c})^{\times }$
, one has
 $W(\mathrm {Ind}_H^G\phi ) = W(\chi _{G/H})$
, where
$W(\mathrm {Ind}_H^G\phi ) = W(\chi _{G/H})$
, where
 $\chi _{G/H}$
is the nontrivial character of
$\chi _{G/H}$
is the nontrivial character of
 $G/H$
.
$G/H$
.
Proof It is enough to prove claim (a) in the case where
![]() $\phi $
is a character of G, represented by a homomorphism
$\phi $
is a character of G, represented by a homomorphism
![]() $T_\phi : G \to \mathrm {GL}_d({\mathbf Q}^{c})$
. In this case, the general result of [Reference Martinet and Fröhlich18, Chapter II, Section 4, Corollary] implies that
$T_\phi : G \to \mathrm {GL}_d({\mathbf Q}^{c})$
. In this case, the general result of [Reference Martinet and Fröhlich18, Chapter II, Section 4, Corollary] implies that
where
![]() $\mathrm {det}_\phi $
is the homomorphism
$\mathrm {det}_\phi $
is the homomorphism
![]() $G^{\mathrm {ab}} \to ({\mathbf Q}^{c})^{\times }$
induced by sending each g in G to
$G^{\mathrm {ab}} \to ({\mathbf Q}^{c})^{\times }$
induced by sending each g in G to
![]() $\mathrm {det}(T_\phi (g))$
and
$\mathrm {det}(T_\phi (g))$
and
![]() $\rho _F$
is the reciprocity map
$\rho _F$
is the reciprocity map
![]() $F^\times \to G^{\mathrm {ab}}$
. In addition,
$F^\times \to G^{\mathrm {ab}}$
. In addition,
![]() $-1$
belongs to
$-1$
belongs to
![]() $O^\times _{F}$
and so is sent by
$O^\times _{F}$
and so is sent by
![]() $\rho _F$
to an element of the inertia subgroup of
$\rho _F$
to an element of the inertia subgroup of
![]() $G^{\mathrm {ab}}$
of order dividing 2. In particular, since this inertia group has odd order, one has
$G^{\mathrm {ab}}$
of order dividing 2. In particular, since this inertia group has odd order, one has
![]() $\rho _F(-1) = 1$
and so
$\rho _F(-1) = 1$
and so
![]() $\mathrm {det}_{\phi }(\rho _F(-1))=1$
. This proves claim (a).
$\mathrm {det}_{\phi }(\rho _F(-1))=1$
. This proves claim (a).
To prove part (b), we use the inductivity of local root numbers in degree zero to compute
 $$ \begin{align*}W(\mathrm{Ind}_H^G\phi) =&\, W(\mathrm{Ind}_{H}^{G}(\phi - \phi(1)\mathbf{1}_H))W(\mathrm{Ind}_H^G1_H)^{\phi(1)}\\ =&\, W(\phi - \mathbf{1}_H)W(\mathrm{Ind}_{H}^G\mathbf{1}_H)^{\phi(1)}\\ =&\, W(\phi)W(\mathbf{1}_H)^{-1}\prod_{\theta\in (G/H)^*}W(\theta)^{\phi(1)},\end{align*} $$
$$ \begin{align*}W(\mathrm{Ind}_H^G\phi) =&\, W(\mathrm{Ind}_{H}^{G}(\phi - \phi(1)\mathbf{1}_H))W(\mathrm{Ind}_H^G1_H)^{\phi(1)}\\ =&\, W(\phi - \mathbf{1}_H)W(\mathrm{Ind}_{H}^G\mathbf{1}_H)^{\phi(1)}\\ =&\, W(\phi)W(\mathbf{1}_H)^{-1}\prod_{\theta\in (G/H)^*}W(\theta)^{\phi(1)},\end{align*} $$
where
![]() $(G/H)^*$
denotes the group of homomorphisms
$(G/H)^*$
denotes the group of homomorphisms
![]() $G/H \to ({\mathbf Q}^{c})^{\times }$
, and the last equality is true because
$G/H \to ({\mathbf Q}^{c})^{\times }$
, and the last equality is true because
![]() $\mathrm {Ind}_H^G\mathbf {1}_H$
is equal to the sum of
$\mathrm {Ind}_H^G\mathbf {1}_H$
is equal to the sum of
![]() $\theta $
over
$\theta $
over
![]() $(G/H)^*$
. Now, if
$(G/H)^*$
. Now, if
![]() $G/H$
is odd (resp. even), then the only real-valued functions in
$G/H$
is odd (resp. even), then the only real-valued functions in
![]() $(G/H)^*$
are
$(G/H)^*$
are
![]() $\mathbf {1}_G$
(resp.
$\mathbf {1}_G$
(resp.
![]() $\mathbf {1}_G$
and
$\mathbf {1}_G$
and
![]() $\chi _{G/H}$
) and all other homomorphisms occur in complex conjugate pairs. The result of part (b) therefore follows from the above displayed formula after isolating the conjugate pairs in the product that occurs in the final term, applying the result of part (a) to each of these pairs, and noting that
$\chi _{G/H}$
) and all other homomorphisms occur in complex conjugate pairs. The result of part (b) therefore follows from the above displayed formula after isolating the conjugate pairs in the product that occurs in the final term, applying the result of part (a) to each of these pairs, and noting that
![]() $W(\mathbf {1}_H) = W(\mathbf {1}_G) = 1$
.
$W(\mathbf {1}_H) = W(\mathbf {1}_G) = 1$
.
To prove part (c), we recall that by a result of Fröhlich and Queyrut [Reference Fröhlich and Queyrut16, Section 4, Theorem 3], one has
![]() $W(\phi ) = \phi (\rho _L(x))$
, where
$W(\phi ) = \phi (\rho _L(x))$
, where
![]() $\rho _L$
is the reciprocity map
$\rho _L$
is the reciprocity map
![]() $L^\times \to H$
and x is any element of
$L^\times \to H$
and x is any element of
![]() $L\setminus F$
with
$L\setminus F$
with
![]() $x^2 \in F^\times $
. In addition, since
$x^2 \in F^\times $
. In addition, since
![]() $\phi $
is of dihedral type, it is trivial on restriction to
$\phi $
is of dihedral type, it is trivial on restriction to
![]() $F^\times $
(cf. [Reference Fröhlich and Queyrut16, Section 3, Lemma 1]) and so
$F^\times $
(cf. [Reference Fröhlich and Queyrut16, Section 3, Lemma 1]) and so
![]() $\phi (\rho _L(x))^2 = \phi (\rho _L(x^2)) = \phi (1) = 1$
. On the other hand, the order of
$\phi (\rho _L(x))^2 = \phi (\rho _L(x^2)) = \phi (1) = 1$
. On the other hand, the order of
![]() $\phi $
is odd (since it divides
$\phi $
is odd (since it divides
![]() $|H| = |G|/2$
which, under the given hypothesis on
$|H| = |G|/2$
which, under the given hypothesis on
![]() $|G|$
, is odd) and so
$|G|$
, is odd) and so
![]() $\phi (\rho _L(x))^2 = 1$
implies
$\phi (\rho _L(x))^2 = 1$
implies
![]() $\phi (\rho _L(x)) =1$
and hence also
$\phi (\rho _L(x)) =1$
and hence also
![]() $W(\phi )=1$
.
$W(\phi )=1$
.
This last equality then combines with a straightforward application of the general result of part (b) to prove the formula in part (c).
We are now ready to prove Theorem 7.2. At the outset, we note that G is the semidirect product of its inertia subgroup I by the cyclic quotient group
![]() $G/I$
. We further note that, by assumption, the group I is cyclic of odd order, and hence, in particular, that G is supersolvable.
$G/I$
. We further note that, by assumption, the group I is cyclic of odd order, and hence, in particular, that G is supersolvable.
Fix
![]() $\chi $
in
$\chi $
in
![]() $\mathrm {Symp}(G)$
. Then, since
$\mathrm {Symp}(G)$
. Then, since
![]() $\chi $
is tamely ramified, one has
$\chi $
is tamely ramified, one has
![]() $W(\chi )\in \{\pm 1\}$
(cf. [Reference Fröhlich14, Chapter III, Theorem 21(iii)]) and so
$W(\chi )\in \{\pm 1\}$
(cf. [Reference Fröhlich14, Chapter III, Theorem 21(iii)]) and so
![]() $W(2\chi ) = W(\chi )^2 = 1$
. It is therefore enough for us to prove that
$W(2\chi ) = W(\chi )^2 = 1$
. It is therefore enough for us to prove that
![]() $W(\psi _2(\chi )) = 1$
.
$W(\psi _2(\chi )) = 1$
.
Next, we note that, by Lemma 7.3(c)(i), there exists a subgroup J of G that contains I and a linear character
![]() $\phi $
of J such that one has
$\phi $
of J such that one has
![]() $\chi = \mathrm {Ind}_{J}^G\phi $
. In particular, since J contains I and
$\chi = \mathrm {Ind}_{J}^G\phi $
. In particular, since J contains I and
![]() $G/I$
is cyclic, there exists a normal subgroup H of G with
$G/I$
is cyclic, there exists a normal subgroup H of G with
![]() $J \trianglelefteq H \trianglelefteq G$
and such that
$J \trianglelefteq H \trianglelefteq G$
and such that
![]() $H/J$
is cyclic of
$H/J$
is cyclic of
![]() $2$
-power order and
$2$
-power order and
![]() $G/H$
is cyclic of odd order.
$G/H$
is cyclic of odd order.
Then one has
![]() $\chi = \mathrm {Ind}_H^G\chi '$
with
$\chi = \mathrm {Ind}_H^G\chi '$
with
![]() $\chi ' := \mathrm {Ind}_J^H\phi $
and we claim that
$\chi ' := \mathrm {Ind}_J^H\phi $
and we claim that
![]() $\chi '$
belongs to
$\chi '$
belongs to
![]() $\mathrm {Symp}(H)$
. To see this, we note that
$\mathrm {Symp}(H)$
. To see this, we note that
![]() $\chi '$
is an irreducible character of H (since
$\chi '$
is an irreducible character of H (since
![]() $\chi $
is irreducible) and so, by the Frobenius–Schur theorem (cf. [Reference Curtis and Reiner9, Theorem (73.13)]), the sum
$\chi $
is irreducible) and so, by the Frobenius–Schur theorem (cf. [Reference Curtis and Reiner9, Theorem (73.13)]), the sum
![]() $c_H(\chi ') := |H|^{-1}\sum _{h \in H}\chi (h^2)$
belongs to
$c_H(\chi ') := |H|^{-1}\sum _{h \in H}\chi (h^2)$
belongs to
![]() $\{-1, 0, 1\}$
and is equal to
$\{-1, 0, 1\}$
and is equal to
![]() $-1$
if and only if
$-1$
if and only if
![]() $\chi '$
is symplectic. In addition, since H is normal in G and of odd index, one has
$\chi '$
is symplectic. In addition, since H is normal in G and of odd index, one has
![]() $g^2 \in H \Longleftrightarrow g \in H$
for each
$g^2 \in H \Longleftrightarrow g \in H$
for each
![]() $g \in G$
and so
$g \in G$
and so
 $$ \begin{align*}c_G(\chi) = c_G(\mathrm{Ind}_H^G\chi') =&\, |G|^{-1}\sum_{g \in G}(\mathrm{Ind}_H^G\chi')(g^2)\\ =&\, |G|^{-1}\sum_{\tau \in \mathcal{T}}\sum_{h \in H}(\chi')^\tau(h^2)\\ =&\, |\mathcal{T}|^{-1}\sum_{\tau\in \mathcal{T}}c_H((\chi')^\tau),\end{align*} $$
$$ \begin{align*}c_G(\chi) = c_G(\mathrm{Ind}_H^G\chi') =&\, |G|^{-1}\sum_{g \in G}(\mathrm{Ind}_H^G\chi')(g^2)\\ =&\, |G|^{-1}\sum_{\tau \in \mathcal{T}}\sum_{h \in H}(\chi')^\tau(h^2)\\ =&\, |\mathcal{T}|^{-1}\sum_{\tau\in \mathcal{T}}c_H((\chi')^\tau),\end{align*} $$
where
![]() $\mathcal {T}$
is a set of coset representatives of H in G and
$\mathcal {T}$
is a set of coset representatives of H in G and
![]() $(\chi ')^\tau $
is the irreducible character of H that sends each element h to
$(\chi ')^\tau $
is the irreducible character of H that sends each element h to
![]() $\chi '(h^\tau )$
. In particular, since both
$\chi '(h^\tau )$
. In particular, since both
![]() $c_G(\chi ) = -1$
(as
$c_G(\chi ) = -1$
(as
![]() $\chi \in \mathrm {Symp}(G)$
) and each
$\chi \in \mathrm {Symp}(G)$
) and each
![]() $c_H((\chi ')^\tau )$
belongs to
$c_H((\chi ')^\tau )$
belongs to
![]() $\{-1,0,1\}$
, the displayed equality implies that
$\{-1,0,1\}$
, the displayed equality implies that
![]() $c_H((\chi ')^\tau ) = -1$
for all
$c_H((\chi ')^\tau ) = -1$
for all
![]() $\tau $
. Thus, one has
$\tau $
. Thus, one has
![]() $c_H(\chi ') = -1$
and so
$c_H(\chi ') = -1$
and so
![]() $\chi ' \in \mathrm {Symp}(H)$
, as claimed.
$\chi ' \in \mathrm {Symp}(H)$
, as claimed.
Now, since
![]() $G/H$
is cyclic of odd order, one has
$G/H$
is cyclic of odd order, one has
![]() $W(\psi _2(\chi )) = W(\mathrm {Ind}_H^G(\psi _2(\chi ')) = W(\psi _2(\chi '))$
, where the first equality follows from Lemma 7.3(b) and the second from Proposition 7.4(b). Thus, if necessary after replacing G by H (and
$W(\psi _2(\chi )) = W(\mathrm {Ind}_H^G(\psi _2(\chi ')) = W(\psi _2(\chi '))$
, where the first equality follows from Lemma 7.3(b) and the second from Proposition 7.4(b). Thus, if necessary after replacing G by H (and
![]() $\chi $
by
$\chi $
by
![]() $\chi '$
), we can assume in the sequel that
$\chi '$
), we can assume in the sequel that
![]() $\chi $
has
$\chi $
has
![]() $2$
-power degree.
$2$
-power degree.
Next, we note that, since G is supersolvable, an induction theorem of Martinet (cf. [Reference Martinet and Fröhlich18, Chapter III, Theorem 5.2]) implies that either
![]() $\chi = \mathrm {Tr}(\mathrm {Ind}_{H'}^G\phi ')$
, where
$\chi = \mathrm {Tr}(\mathrm {Ind}_{H'}^G\phi ')$
, where
![]() $\phi '$
is a linear character of some subgroup
$\phi '$
is a linear character of some subgroup
![]() $H'$
of G, or that
$H'$
of G, or that
![]() $\chi $
is the induction to G of a quaternion character of a subgroup. In view of Proposition 7.4(a), we can therefore also assume in the sequel that there exists a subgroup
$\chi $
is the induction to G of a quaternion character of a subgroup. In view of Proposition 7.4(a), we can therefore also assume in the sequel that there exists a subgroup
![]() $J_1$
of G that has
$J_1$
of G that has
![]() $2$
-power index, and hence contains I, and a quaternion character
$2$
-power index, and hence contains I, and a quaternion character
![]() $\phi _1$
of
$\phi _1$
of
![]() $J_1$
such that
$J_1$
such that
![]() $\chi = \mathrm {Ind}_{J_1}^G\phi _1$
.
$\chi = \mathrm {Ind}_{J_1}^G\phi _1$
.
This implies that
![]() $J_1$
has a quotient Q isomorphic to a generalized quaternion group and that
$J_1$
has a quotient Q isomorphic to a generalized quaternion group and that
where P is the cyclic subgroup of Q of index
![]() $2$
and
$2$
and
![]() $\theta $
a homomorphism
$\theta $
a homomorphism
![]() $P\to ({\mathbf Q}^{c})^{\times }$
. Let
$P\to ({\mathbf Q}^{c})^{\times }$
. Let
![]() $J_1'$
denote the inverse image of P under the quotient map
$J_1'$
denote the inverse image of P under the quotient map
![]() $J_1 \to Q$
, and set
$J_1 \to Q$
, and set
![]() $\phi _1':= \mathrm { Inf}^{J_1'}_{P} \theta $
(so
$\phi _1':= \mathrm { Inf}^{J_1'}_{P} \theta $
(so
![]() $\phi _1'$
is a linear character of
$\phi _1'$
is a linear character of
![]() $J_1'$
). Then the subgroup
$J_1'$
). Then the subgroup
![]() $J_1'$
is of index
$J_1'$
is of index
![]() $2$
in
$2$
in
![]() $J_1$
, and (7.4) implies that
$J_1$
, and (7.4) implies that
Now, as
![]() $J_1'$
has
$J_1'$
has
![]() $2$
-power index in G, it contains I. Thus, since
$2$
-power index in G, it contains I. Thus, since
![]() $G/I$
is cyclic, one has
$G/I$
is cyclic, one has
![]() $J_1' \trianglelefteq G$
and
$J_1' \trianglelefteq G$
and
![]() $G/J_1'$
is cyclic of
$G/J_1'$
is cyclic of
![]() $2$
-power order. In particular, since the degree
$2$
-power order. In particular, since the degree
![]() $(\psi _2(\phi _1))(1) = \phi _1(1)$
is even, one therefore has
$(\psi _2(\phi _1))(1) = \phi _1(1)$
is even, one therefore has
where the second equality follows from Lemma 7.3(c)(iii) (after taking account of (7.5)) and the third from Proposition 7.4(b).
In addition, since Q is the Galois group of a tamely ramified extension of p-adic fields that has odd ramification degree, it is the semidirect product of a cyclic (inertia) subgroup of odd order by a cyclic group. In particular, since such a group can have no quotient isomorphic to
![]() $H_8$
, the group Q must be isomorphic to
$H_8$
, the group Q must be isomorphic to
![]() $H_{4m}$
, with m odd. In view of (7.4), we can therefore apply Lemma 7.3(d) (with
$H_{4m}$
, with m odd. In view of (7.4), we can therefore apply Lemma 7.3(d) (with
![]() $\Gamma , \Delta $
, and
$\Gamma , \Delta $
, and
![]() $\phi $
taken to be
$\phi $
taken to be
![]() $Q, P$
, and
$Q, P$
, and
![]() $\theta $
) to deduce that
$\theta $
) to deduce that
where N denotes the center of Q (so N is the unique subgroup of P of order 2) and
![]() $\lambda $
denotes
$\lambda $
denotes
![]() $\theta ^2$
, regarded as a homomorphism
$\theta ^2$
, regarded as a homomorphism
![]() $P/N \to ({\mathbf Q}^{c})^{\times }$
.
$P/N \to ({\mathbf Q}^{c})^{\times }$
.
Finally, since the group
![]() $Q/N$
is generalized dihedral with
$Q/N$
is generalized dihedral with
![]() $|Q/N| = 2m \equiv 2$
modulo
$|Q/N| = 2m \equiv 2$
modulo
![]() $4$
, and the inertia subgroup of
$4$
, and the inertia subgroup of
![]() $Q/N$
has odd order, the theorem of Fröhlich and Queyrut implies (via Proposition 7.4(c)) that
$Q/N$
has odd order, the theorem of Fröhlich and Queyrut implies (via Proposition 7.4(c)) that
![]() $W(\mathrm {Ind}_{P/N}^{Q/N}(\lambda )) = W(\chi _{Q/P})$
. Upon substituting this fact into the last two displayed formulas, we deduce that
$W(\mathrm {Ind}_{P/N}^{Q/N}(\lambda )) = W(\chi _{Q/P})$
. Upon substituting this fact into the last two displayed formulas, we deduce that
![]() $W(\psi _2(\chi )) = W(\chi _{Q/P})^2 = 1$
.
$W(\psi _2(\chi )) = W(\chi _{Q/P})^2 = 1$
.
This completes the proof of Theorem 7.1.
8 Symplectic Galois–Jacobi sums II
We retain the notation of the previous two sections. For any real number x, we write
![]() $\operatorname {\mathrm {sgn}}(x) \in \{ \pm 1\}$
for the sign of x. In this section, we shall examine
$\operatorname {\mathrm {sgn}}(x) \in \{ \pm 1\}$
for the sign of x. In this section, we shall examine
![]() $\operatorname {\mathrm {sgn}}(J^*(L_\pi /L, \chi ))$
for
$\operatorname {\mathrm {sgn}}(J^*(L_\pi /L, \chi ))$
for
![]() $\chi \in \operatorname {\mathrm {Symp}}(G)$
. This will in turn lead to the definition of
$\chi \in \operatorname {\mathrm {Symp}}(G)$
. This will in turn lead to the definition of
![]() ${\mathcal J}^{\ast }_\infty (F_\pi /F) \in \operatorname {\mathrm {Cl}}({\mathbf Z} G)$
for F a number field and
${\mathcal J}^{\ast }_\infty (F_\pi /F) \in \operatorname {\mathrm {Cl}}({\mathbf Z} G)$
for F a number field and
![]() $[\pi ] \in H^1_t(F,G)$
.
$[\pi ] \in H^1_t(F,G)$
.
Recall that for each
![]() $\chi \in R_G$
, the adjusted Galois–Gauss sum is defined (in [Reference Fröhlich14, Chapter IV, Section 1]) by setting
$\chi \in R_G$
, the adjusted Galois–Gauss sum is defined (in [Reference Fröhlich14, Chapter IV, Section 1]) by setting
for suitable roots of unity
![]() $y(L, \chi )$
and
$y(L, \chi )$
and
![]() $z(L,\chi )$
in
$z(L,\chi )$
in
![]() ${\mathbf Q}^c$
. [Reference Fröhlich14, Chapter IV, Theorem 29(i)] implies that
${\mathbf Q}^c$
. [Reference Fröhlich14, Chapter IV, Theorem 29(i)] implies that
![]() $y(L,\chi ) =1$
for all
$y(L,\chi ) =1$
for all
![]() $\chi $
in
$\chi $
in
![]() $\mathrm {Symp}(G)$
. One can also check (directly from the definitions) that
$\mathrm {Symp}(G)$
. One can also check (directly from the definitions) that
![]() $z(L,\psi _2(\chi )) = z(L,\chi )^2$
and hence that
$z(L,\psi _2(\chi )) = z(L,\chi )^2$
and hence that
![]() $z(L,\chi ) = z(L,\psi _2(\chi )) = 1$
for each
$z(L,\chi ) = z(L,\psi _2(\chi )) = 1$
for each
![]() $\chi $
in
$\chi $
in
![]() $\mathrm { Symp}(G)$
.
$\mathrm { Symp}(G)$
.
Recall that Theorem 7.1 asserts that
![]() $J(L_\pi /L, \chi )>0$
whenever
$J(L_\pi /L, \chi )>0$
whenever
![]() $\chi \in \operatorname {\mathrm {Symp}}(G)$
. The following result is now a direct consequence of the definition of the adjusted Galois–Jacobi sum
$\chi \in \operatorname {\mathrm {Symp}}(G)$
. The following result is now a direct consequence of the definition of the adjusted Galois–Jacobi sum
![]() $J^*(L_\pi /L, \chi )$
.
$J^*(L_\pi /L, \chi )$
.
Theorem 8.1 Suppose that
![]() $\chi \in \operatorname {\mathrm {Symp}}(G)$
. Then
$\chi \in \operatorname {\mathrm {Symp}}(G)$
. Then
The following Propostion shows that
![]() $\operatorname {\mathrm {sgn}}(y(L_\pi /L, \psi _2(\chi ))) = -1$
is possible.
$\operatorname {\mathrm {sgn}}(y(L_\pi /L, \psi _2(\chi ))) = -1$
is possible.
Proposition 8.2 Let
![]() $M/L$
be a tamely ramified Galois extension with
$M/L$
be a tamely ramified Galois extension with
![]() $\Gamma := \operatorname {\mathrm {Gal}}(M/L) \simeq H_{4m}$
, with m odd. Suppose that the inertia subgroup
$\Gamma := \operatorname {\mathrm {Gal}}(M/L) \simeq H_{4m}$
, with m odd. Suppose that the inertia subgroup
![]() $\Gamma _{0}$
of
$\Gamma _{0}$
of
![]() $\Gamma $
is odd. Then, for each
$\Gamma $
is odd. Then, for each
![]() $\chi \in \operatorname {\mathrm {Symp}}(G)$
, we have
$\chi \in \operatorname {\mathrm {Symp}}(G)$
, we have
![]() $y(M/L, \psi _2(\chi )) = -1$
.
$y(M/L, \psi _2(\chi )) = -1$
.
Proof For ease of notation, we write, e.g.,
![]() $y(\chi )$
rather than
$y(\chi )$
rather than
![]() $y(M/L,\chi )$
.
$y(M/L,\chi )$
.
To prove the desired result, we shall use Lemma 7.3. Let
![]() $\Delta $
be the cyclic subgroup of
$\Delta $
be the cyclic subgroup of
![]() $\Gamma $
of index
$\Gamma $
of index
![]() $2$
. Then all irreducible symplectic characters of
$2$
. Then all irreducible symplectic characters of
![]() $\Gamma $
can be written in the form
$\Gamma $
can be written in the form
![]() $\chi =\mathrm {Ind}_\Delta ^{\Gamma }\phi $
, where
$\chi =\mathrm {Ind}_\Delta ^{\Gamma }\phi $
, where
![]() $\phi $
is a linear character of
$\phi $
is a linear character of
![]() $\Delta $
. It is easy to see that the order of
$\Delta $
. It is easy to see that the order of
![]() $\phi $
does not divide
$\phi $
does not divide
![]() $2$
(for otherwise
$2$
(for otherwise
![]() $\mathrm {Ind}_\Delta ^{\Gamma }\phi $
would be an orthogonal character of
$\mathrm {Ind}_\Delta ^{\Gamma }\phi $
would be an orthogonal character of
![]() $\Gamma $
; see [Reference Martinet and Fröhlich18, Chapter III, Theorem 3.1]), and that
$\Gamma $
; see [Reference Martinet and Fröhlich18, Chapter III, Theorem 3.1]), and that
![]() $\phi $
(and hence also
$\phi $
(and hence also
![]() $\phi ^2$
) is nontrivial on
$\phi ^2$
) is nontrivial on
![]() $\Gamma _{0}$
(since
$\Gamma _{0}$
(since
![]() $\Gamma _{0}$
has odd order).
$\Gamma _{0}$
has odd order).
Let Z denote the center of
![]() $\Gamma $
, and let
$\Gamma $
, and let
![]() $\chi _{\Gamma /\Delta }$
denote the unique nontrivial homomorphism
$\chi _{\Gamma /\Delta }$
denote the unique nontrivial homomorphism
![]() $\Gamma /\Delta \rightarrow ({\mathbf Q}^{c})^{\times }$
. Using the formula in Lemma 7.3(d), one can compute that
$\Gamma /\Delta \rightarrow ({\mathbf Q}^{c})^{\times }$
. Using the formula in Lemma 7.3(d), one can compute that
 $$ \begin{align*} y(\psi_{2}(\chi)) =&\, y(\psi_2(\mathrm{Ind}_\Delta^{\Gamma} \phi))\\ =&\, y( \mathrm{Inf}_{\Gamma/Z}^{\Gamma}(\mathrm{Ind}_{\Delta/Z}^{\Gamma/Z}(\phi^2))) \cdot y( \mathrm{Inf}_{\Gamma/\Delta}^{\Gamma}(\chi_{\Gamma/\Delta})) \cdot y( \mathbf{1}_{\Gamma})^{-1} \\ =&\, (-1)^{\deg(n_0)}\mathrm{det}_{n_0}(\sigma) \cdot (-1)\chi_{\Gamma/\Delta}(\sigma) \cdot (-1) \mathbf{1}_{\Gamma}(\sigma)^{-1}\\ =&\, 1 \cdot 1 \cdot (-1) = -1, \end{align*} $$
$$ \begin{align*} y(\psi_{2}(\chi)) =&\, y(\psi_2(\mathrm{Ind}_\Delta^{\Gamma} \phi))\\ =&\, y( \mathrm{Inf}_{\Gamma/Z}^{\Gamma}(\mathrm{Ind}_{\Delta/Z}^{\Gamma/Z}(\phi^2))) \cdot y( \mathrm{Inf}_{\Gamma/\Delta}^{\Gamma}(\chi_{\Gamma/\Delta})) \cdot y( \mathbf{1}_{\Gamma})^{-1} \\ =&\, (-1)^{\deg(n_0)}\mathrm{det}_{n_0}(\sigma) \cdot (-1)\chi_{\Gamma/\Delta}(\sigma) \cdot (-1) \mathbf{1}_{\Gamma}(\sigma)^{-1}\\ =&\, 1 \cdot 1 \cdot (-1) = -1, \end{align*} $$
where
![]() $\phi ^2$
is regarded as a character of
$\phi ^2$
is regarded as a character of
![]() $\Delta /Z$
,
$\Delta /Z$
,
![]() $\sigma $
is the Frobenius element in
$\sigma $
is the Frobenius element in
![]() $\Gamma /\Gamma _{0}$
lifted to
$\Gamma /\Gamma _{0}$
lifted to
![]() $\Gamma $
, and
$\Gamma $
, and
![]() $n_0:= n(\mathrm {Inf}_{\Gamma /Z}^{\Gamma }(\mathrm {Ind}_{\Delta /Z}^{\Gamma /Z}(\phi ^2)))$
denotes the unramified part (cf. [Reference Fröhlich14, Chapter I, equation (5.6)]) of
$n_0:= n(\mathrm {Inf}_{\Gamma /Z}^{\Gamma }(\mathrm {Ind}_{\Delta /Z}^{\Gamma /Z}(\phi ^2)))$
denotes the unramified part (cf. [Reference Fröhlich14, Chapter I, equation (5.6)]) of
![]() $\mathrm {Inf}_{\Gamma /Z}^{\Gamma }(\mathrm {Ind}_{\Delta /Z}^{\Gamma /Z}(\phi ^2))$
. The third equality above holds since clearly
$\mathrm {Inf}_{\Gamma /Z}^{\Gamma }(\mathrm {Ind}_{\Delta /Z}^{\Gamma /Z}(\phi ^2))$
. The third equality above holds since clearly
![]() $\mathrm {Inf}_{\Gamma /\Delta }^{\Gamma }(\chi _{\Gamma /\Delta })$
and
$\mathrm {Inf}_{\Gamma /\Delta }^{\Gamma }(\chi _{\Gamma /\Delta })$
and
![]() $\mathbf {1}_{\Gamma }$
are both linear and unramified. The fourth equality follows from the fact that
$\mathbf {1}_{\Gamma }$
are both linear and unramified. The fourth equality follows from the fact that
![]() $n_0=0$
(since
$n_0=0$
(since
![]() $\phi ^2$
is irreducible and ramified, by [Reference Fröhlich14, Chapter III, Proposition 1.3(ii)] the unramified part
$\phi ^2$
is irreducible and ramified, by [Reference Fröhlich14, Chapter III, Proposition 1.3(ii)] the unramified part
![]() $n(\mathrm {Ind}_{\Delta /Z}^{\Gamma /Z}(\phi ^2))=0$
and therefore
$n(\mathrm {Ind}_{\Delta /Z}^{\Gamma /Z}(\phi ^2))=0$
and therefore
![]() $n_0=0$
).
$n_0=0$
).
The above discussion motivates the following definition.
Definition 8.3 We define
![]() $J^{*}_{\infty }(L_\pi /L,-) \in \operatorname {\mathrm {Hom}}_{\Omega _{{\mathbf Q}}}(R_G, J({\mathbf Q}^c))$
by its values on
$J^{*}_{\infty }(L_\pi /L,-) \in \operatorname {\mathrm {Hom}}_{\Omega _{{\mathbf Q}}}(R_G, J({\mathbf Q}^c))$
by its values on
![]() $\chi \in \operatorname {\mathrm {Irr}}(G)$
as follows:
$\chi \in \operatorname {\mathrm {Irr}}(G)$
as follows:
 $$\begin{align*}J^{*}_{\infty}(L_\pi/L, \chi)_v = \begin{cases} \operatorname{\mathrm{sgn}}(J^{*}(L_\pi/L, \chi)), \quad &\text{if }\chi \in \operatorname{\mathrm{Symp}}(G) \text{ and }v|\infty,\\ 1, \quad &\text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}J^{*}_{\infty}(L_\pi/L, \chi)_v = \begin{cases} \operatorname{\mathrm{sgn}}(J^{*}(L_\pi/L, \chi)), \quad &\text{if }\chi \in \operatorname{\mathrm{Symp}}(G) \text{ and }v|\infty,\\ 1, \quad &\text{otherwise.} \end{cases} \end{align*}$$
We write
![]() $J^{*}_{\infty }(L_\pi /L)$
for the element of
$J^{*}_{\infty }(L_\pi /L)$
for the element of
![]() $K_{0}({\mathbf Z} G, {\mathbf Q})$
represented by the homomorphism
$K_{0}({\mathbf Z} G, {\mathbf Q})$
represented by the homomorphism
![]() $J^{*}_{\infty }(L_\pi /L,-)$
. Similarly, we also write
$J^{*}_{\infty }(L_\pi /L,-)$
. Similarly, we also write
![]() $J^{*}(L_\pi /L)$
for the element of
$J^{*}(L_\pi /L)$
for the element of
![]() $K_{0}({\mathbf Z} G, {\mathbf Q})$
represented by
$K_{0}({\mathbf Z} G, {\mathbf Q})$
represented by
![]() $J^{*}(L_\pi /L,-)$
.
$J^{*}(L_\pi /L,-)$
.
Theorem 8.4 We have
and so
Proof To ease notation, set
![]() $f = J^{*}(L_{\pi }/L,-) \cdot J^{*}_{\infty }(L_{\pi }/L,-)^{-1} $
.
$f = J^{*}(L_{\pi }/L,-) \cdot J^{*}_{\infty }(L_{\pi }/L,-)^{-1} $
.
Then, since
![]() $f \in \operatorname {\mathrm {Hom}}_{\Omega _{{\mathbf Q}}}(R_G, ({\mathbf Q}^{c})^{\times })$
, the Hasse–Schilling–Maass Norm Theorem (cf. [Reference Curtis and Reiner8, Theorem (7.48)]) implies that the first equality is equivalent to asserting that
$f \in \operatorname {\mathrm {Hom}}_{\Omega _{{\mathbf Q}}}(R_G, ({\mathbf Q}^{c})^{\times })$
, the Hasse–Schilling–Maass Norm Theorem (cf. [Reference Curtis and Reiner8, Theorem (7.48)]) implies that the first equality is equivalent to asserting that
![]() $f(\chi )$
is a strictly positive real number for every
$f(\chi )$
is a strictly positive real number for every
![]() $\chi $
in
$\chi $
in
![]() $\operatorname {\mathrm {Symp}}(G)$
. This in turn follows at once from the definition of
$\operatorname {\mathrm {Symp}}(G)$
. This in turn follows at once from the definition of
![]() $J^{*}_{\infty }(L_{\pi }/L,-)$
.
$J^{*}_{\infty }(L_{\pi }/L,-)$
.
The second equality is now an immediate consequence of the fact that
![]() $\partial ^0(\operatorname {\mathrm {Det}}({\mathbf Q}^c G)) = 0$
.
$\partial ^0(\operatorname {\mathrm {Det}}({\mathbf Q}^c G)) = 0$
.
Suppose now that F is a number field and that
![]() $[\pi ] \in H^1_t(F, G)$
. We also recall that
$[\pi ] \in H^1_t(F, G)$
. We also recall that
![]() $F_{\pi , v}:= F_{\pi } \otimes _{F} F_{v} \simeq F_{v, \pi _v}$
(see, e.g., [Reference McCulloh19, equation (2.4)]).
$F_{\pi , v}:= F_{\pi } \otimes _{F} F_{v} \simeq F_{v, \pi _v}$
(see, e.g., [Reference McCulloh19, equation (2.4)]).
Definition 8.5 We set
and
(Note that the infinite sums make sense as
![]() $J^{*}_{\infty }(F_{v,\pi _{v}}/F_{v}) = J^{*}(F_{v,\pi _{v}}/F_{v}) =0$
for all places v that are unramified in
$J^{*}_{\infty }(F_{v,\pi _{v}}/F_{v}) = J^{*}(F_{v,\pi _{v}}/F_{v}) =0$
for all places v that are unramified in
![]() $F_{\pi }/F$
.)
$F_{\pi }/F$
.)
We define
![]() ${\mathcal J}^*(F_{\pi }/F) \in \operatorname {\mathrm {Cl}}({\mathbf Z} G)$
by
${\mathcal J}^*(F_{\pi }/F) \in \operatorname {\mathrm {Cl}}({\mathbf Z} G)$
by
(see (2.2)).
Proposition 8.6 Suppose that F is a number field and that
![]() $[\pi ] \in H^1_t(F,G)$
. Then
$[\pi ] \in H^1_t(F,G)$
. Then
9 Proof of Theorem 1.5
Let
![]() $[\pi ] \in H^1_t(F,G)$
, and write
$[\pi ] \in H^1_t(F,G)$
, and write
For each finite place v of F, we write
![]() $[\pi _v]$
for the image of
$[\pi _v]$
for the image of
![]() $[\pi ]$
in
$[\pi ]$
in
![]() $H^{1}_{t}(F_v, G)$
.
$H^{1}_{t}(F_v, G)$
.
Recall that
 $$\begin{align*}K_0(O_FG, F) \simeq \frac{\operatorname{\mathrm{Hom}}_{\Omega_F}(R_G, J_{f}(F^c))}{\prod_{v \nmid \infty} \operatorname{\mathrm{Det}}(O_{F_v}G)^{\times}}. \end{align*}$$
$$\begin{align*}K_0(O_FG, F) \simeq \frac{\operatorname{\mathrm{Hom}}_{\Omega_F}(R_G, J_{f}(F^c))}{\prod_{v \nmid \infty} \operatorname{\mathrm{Det}}(O_{F_v}G)^{\times}}. \end{align*}$$
A representing homomorphism in
![]() $\operatorname {\mathrm {Hom}}_{\Omega _F}(R_G, J_{f}(F^c))$
of
$\operatorname {\mathrm {Hom}}_{\Omega _F}(R_G, J_{f}(F^c))$
of
![]() ${\mathfrak c}(\pi )$
is
${\mathfrak c}(\pi )$
is
![]() $f = (f_{v})_{v}$
defined by
$f = (f_{v})_{v}$
defined by
using the notation of Corollary 5.6. Let
![]() $\operatorname {\mathrm {Ram}}(\pi )$
denote the set of finite places of F at which
$\operatorname {\mathrm {Ram}}(\pi )$
denote the set of finite places of F at which
![]() $F_{\pi }/F$
is ramified. If
$F_{\pi }/F$
is ramified. If
![]() $v \notin \operatorname {\mathrm {Ram}}(\pi )$
, then
$v \notin \operatorname {\mathrm {Ram}}(\pi )$
, then
![]() $s_v =1$
and so
$s_v =1$
and so
![]() $f_v =1$
.
$f_v =1$
.
Definition 9.1 Suppose that
![]() $v \in \operatorname {\mathrm {Ram}}(\pi )$
. Then we define
$v \in \operatorname {\mathrm {Ram}}(\pi )$
. Then we define
![]() ${\mathfrak c}(\pi ;v) \in K_0(O_FG, F)$
to be the element represented by
${\mathfrak c}(\pi ;v) \in K_0(O_FG, F)$
to be the element represented by
![]() $f^{(v)} = (f^{(v)}_{w})_{w} \in \operatorname {\mathrm {Hom}}_{\Omega _F}(R_G, J_{f}(F^c))$
given by
$f^{(v)} = (f^{(v)}_{w})_{w} \in \operatorname {\mathrm {Hom}}_{\Omega _F}(R_G, J_{f}(F^c))$
given by
 $$\begin{align*}f^{(v)}_{w}(\chi) = \begin{cases} f_v(\chi) = {\varpi}_{v}^{\langle \psi_{2}(\chi) - 2\chi, s_{v} \rangle_{G}}, &\text{if }w=v, \\ 1, &\text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}f^{(v)}_{w}(\chi) = \begin{cases} f_v(\chi) = {\varpi}_{v}^{\langle \psi_{2}(\chi) - 2\chi, s_{v} \rangle_{G}}, &\text{if }w=v, \\ 1, &\text{otherwise.} \end{cases} \end{align*}$$
Lemma 9.2 We have
Proof It follows from the definitions that
and this implies the result.
We can now prove Theorem 1.5.
Theorem 9.3 Suppose that
![]() $[\pi ] \in H^{1}_{t}(F, G)$
and that
$[\pi ] \in H^{1}_{t}(F, G)$
and that
![]() $A_{\pi }$
is defined. Then
$A_{\pi }$
is defined. Then
and so there is an equality
i.e., (see (1.1))
in
![]() $\operatorname {\mathrm {Cl}}({\mathbf Z} G)$
.
$\operatorname {\mathrm {Cl}}({\mathbf Z} G)$
.
Proof Lemma 9.2 implies that in order to show that
it suffices to show that
for each
![]() $v \in \operatorname {\mathrm {Ram}}(\pi )$
. Theorem 8.4 implies that this is equivalent to showing that
$v \in \operatorname {\mathrm {Ram}}(\pi )$
. Theorem 8.4 implies that this is equivalent to showing that
for each
![]() $v \in \operatorname {\mathrm {Ram}}(\pi )$
.
$v \in \operatorname {\mathrm {Ram}}(\pi )$
.
We see from the description of
![]() $\mathrm {Cl}({\mathbf Z} G)$
given in Theorem 2.1(a) that this last equality will in turn follow if, for each
$\mathrm {Cl}({\mathbf Z} G)$
given in Theorem 2.1(a) that this last equality will in turn follow if, for each
![]() $v \in \operatorname {\mathrm {Ram}}(\pi )$
, we show that
$v \in \operatorname {\mathrm {Ram}}(\pi )$
, we show that
To show this last inclusion, we first observe that Proposition 6.6(a) implies that the inclusion holds at all rational primes l not lying below v.
For each rational prime l that lies below v, we fix an embedding
![]() $\operatorname {\mathrm {Loc}}_l: {\mathbf Q}^c \to {\mathbf Q}^c_{l}$
and use it to identify
$\operatorname {\mathrm {Loc}}_l: {\mathbf Q}^c \to {\mathbf Q}^c_{l}$
and use it to identify
![]() $\operatorname {\mathrm {Irr}}(\Gamma )$
with
$\operatorname {\mathrm {Irr}}(\Gamma )$
with
![]() $\operatorname {\mathrm {Irr}}_l(\Gamma )$
. We recall in particular that such an isomorphism
$\operatorname {\mathrm {Irr}}_l(\Gamma )$
. We recall in particular that such an isomorphism
![]() $R_G \to R_{G, l}$
in turn induces an isomorphism
$R_G \to R_{G, l}$
in turn induces an isomorphism
![]() $\operatorname {\mathrm {Hom}}_{\Omega _{F}}(R_G, ({\mathbf Q}^c)^{\times }_{l}) \to \operatorname {\mathrm {Hom}}_{\Omega _{F_{v}}}(R_{G, l}, ({\mathbf Q}^c_l)^{\times })$
(cf. [Reference Fröhlich14, Chapter II, Lemma 2.1]). Then, reasoning analogously to the proof of [Reference Fröhlich14, Theorem 19, pp. 114–116], one can deduce from Proposition 6.6(b) that
$\operatorname {\mathrm {Hom}}_{\Omega _{F}}(R_G, ({\mathbf Q}^c)^{\times }_{l}) \to \operatorname {\mathrm {Hom}}_{\Omega _{F_{v}}}(R_{G, l}, ({\mathbf Q}^c_l)^{\times })$
(cf. [Reference Fröhlich14, Chapter II, Lemma 2.1]). Then, reasoning analogously to the proof of [Reference Fröhlich14, Theorem 19, pp. 114–116], one can deduce from Proposition 6.6(b) that
This establishes the desired inclusion at rational primes lying below v and completes the proof of the desired result.
Remark 9.4 Let us make some remarks concerning Theorem 9.3 when
![]() $F_{\pi }/F$
is locally abelian.
$F_{\pi }/F$
is locally abelian.
Suppose that
![]() $v \in \operatorname {\mathrm {Ram}}(\pi )$
. Set
$v \in \operatorname {\mathrm {Ram}}(\pi )$
. Set
![]() $s_v:= \pi (\sigma _v)$
, and write
$s_v:= \pi (\sigma _v)$
, and write
![]() $H_v := \langle s_v \rangle $
. Proposition 5.2(d) with
$H_v := \langle s_v \rangle $
. Proposition 5.2(d) with
![]() $G = H_v$
and Proposition 5.3(b) imply that for each
$G = H_v$
and Proposition 5.3(b) imply that for each
![]() $\chi \in R_{H_v}$
, we have
$\chi \in R_{H_v}$
, we have
 $$ \begin{align*} \langle \chi, s_v \rangle^{*}_{H_v} - \langle \chi, s_v \rangle_{H_v} &= (d(s_v), \chi)_{H_v} \\ &= \langle \psi_2(\chi) - \chi, s_v \rangle_{H_v}. \end{align*} $$
$$ \begin{align*} \langle \chi, s_v \rangle^{*}_{H_v} - \langle \chi, s_v \rangle_{H_v} &= (d(s_v), \chi)_{H_v} \\ &= \langle \psi_2(\chi) - \chi, s_v \rangle_{H_v}. \end{align*} $$
Now, suppose also that
![]() $F_v$
contains a primitive
$F_v$
contains a primitive
![]() $|s_v|$
th root of unity. This implies in particular that the extension
$|s_v|$
th root of unity. This implies in particular that the extension
![]() $F^{\pi _{v}}_{v}/F_v$
is abelian. Let
$F^{\pi _{v}}_{v}/F_v$
is abelian. Let
![]() ${\mathfrak b}(\pi ;v) \in K_0(FH_{v}, F)$
be the element represented by
${\mathfrak b}(\pi ;v) \in K_0(FH_{v}, F)$
be the element represented by
![]() $\rho ^{(v)} = (\rho ^{(v)}_{w})_{w} \in \operatorname {\mathrm {Hom}}_{\Omega _{F}}(R_{H_v}, J_{f}(F^c))$
defined by
$\rho ^{(v)} = (\rho ^{(v)}_{w})_{w} \in \operatorname {\mathrm {Hom}}_{\Omega _{F}}(R_{H_v}, J_{f}(F^c))$
defined by
 $$\begin{align*}\rho^{(v)}_{w}(\chi) = \begin{cases} {\varpi}_{v}^{(d(s_{v}), \chi)_{H_{v}}} = {\varpi}_{v}^{\langle \psi_{2}(\chi) - \chi, s_{v} \rangle_{H_v}}, &\text{if }w=v, \\ 1, &\text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}\rho^{(v)}_{w}(\chi) = \begin{cases} {\varpi}_{v}^{(d(s_{v}), \chi)_{H_{v}}} = {\varpi}_{v}^{\langle \psi_{2}(\chi) - \chi, s_{v} \rangle_{H_v}}, &\text{if }w=v, \\ 1, &\text{otherwise.} \end{cases} \end{align*}$$
Observe that without the hypothesis concerning the number of roots of unity in
![]() $F_v$
, we would only have that
$F_v$
, we would only have that
![]() $\rho ^{(v)} \in \operatorname {\mathrm {Hom}}(R_{H_v}, J_{f}(F^c))$
rather than
$\rho ^{(v)} \in \operatorname {\mathrm {Hom}}(R_{H_v}, J_{f}(F^c))$
rather than
![]() $\rho ^{(v)} \in \operatorname {\mathrm {Hom}}_{\Omega _{F}}(R_{H_v}, J_{f}(F^c))$
. We also see from the definitions of
$\rho ^{(v)} \in \operatorname {\mathrm {Hom}}_{\Omega _{F}}(R_{H_v}, J_{f}(F^c))$
. We also see from the definitions of
![]() ${\mathfrak c}(\pi ;v)$
and
${\mathfrak c}(\pi ;v)$
and
![]() ${\mathfrak b}(\pi ;v)$
(see also (2.7) and (2.9)) that
${\mathfrak b}(\pi ;v)$
(see also (2.7) and (2.9)) that
![]() ${\mathfrak c}(\pi ;v) = \operatorname {\mathrm {Ind}}^{G}_{H_v} {\mathfrak b}(\pi ;v)$
.
${\mathfrak c}(\pi ;v) = \operatorname {\mathrm {Ind}}^{G}_{H_v} {\mathfrak b}(\pi ;v)$
.
Hence, if for every
![]() $v \in \operatorname {\mathrm {Ram}}(\pi )$
,
$v \in \operatorname {\mathrm {Ram}}(\pi )$
,
![]() $F_v$
contains a primitive
$F_v$
contains a primitive
![]() $|s_v|$
th root of unity—which is precisely what happens if
$|s_v|$
th root of unity—which is precisely what happens if
![]() $F_{\pi }/F$
is locally abelian—then we have
$F_{\pi }/F$
is locally abelian—then we have
and so (using (2.10))
 $$ \begin{align*} \partial^0({\mathfrak c}(\pi)) &= \sum_{v \in \operatorname{\mathrm{Ram}}(\pi)} \partial^0(\operatorname{\mathrm{Ind}}^{G}_{H_v} {\mathfrak b}(\pi;v)) \\ &= \sum_{v \in \operatorname{\mathrm{Ram}}(\pi)} \operatorname{\mathrm{Ind}}^{G}_{H_v} \partial^0({\mathfrak b}(\pi;v)) \\ &=0. \end{align*} $$
$$ \begin{align*} \partial^0({\mathfrak c}(\pi)) &= \sum_{v \in \operatorname{\mathrm{Ram}}(\pi)} \partial^0(\operatorname{\mathrm{Ind}}^{G}_{H_v} {\mathfrak b}(\pi;v)) \\ &= \sum_{v \in \operatorname{\mathrm{Ram}}(\pi)} \operatorname{\mathrm{Ind}}^{G}_{H_v} \partial^0({\mathfrak b}(\pi;v)) \\ &=0. \end{align*} $$
We now deduce from Theorem 9.3 that
![]() ${\mathcal J}^*_{\infty }(F_\pi /F) = 0$
.
${\mathcal J}^*_{\infty }(F_\pi /F) = 0$
.
A comparison of (9.2) and (9.1) highlights the crucial difference between the locally abelian case and the general case. In both cases, the class
![]() ${\mathfrak c}(\pi )$
may be decomposed into a sum over the places
${\mathfrak c}(\pi )$
may be decomposed into a sum over the places
![]() $v \in \operatorname {\mathrm {Ram}}(\pi )$
of classes
$v \in \operatorname {\mathrm {Ram}}(\pi )$
of classes
![]() ${\mathfrak c}(\pi ;v) \in K_0(O_FG, F^c)$
. However, in the locally abelian case, these classes
${\mathfrak c}(\pi ;v) \in K_0(O_FG, F^c)$
. However, in the locally abelian case, these classes
![]() ${\mathfrak c}(\pi ;v)$
are induced from cyclic subgroups of G, whereas in the general case, they are not. This is why Theorem 9.3 may be proved in the locally abelian case using abelian Jacobi sums, thereby showing that in this situation
${\mathfrak c}(\pi ;v)$
are induced from cyclic subgroups of G, whereas in the general case, they are not. This is why Theorem 9.3 may be proved in the locally abelian case using abelian Jacobi sums, thereby showing that in this situation
![]() ${\mathcal J}^*_\infty (F_\pi /F) = 0$
), which is what is done in [Reference Caputo and Vinatier4].
${\mathcal J}^*_\infty (F_\pi /F) = 0$
), which is what is done in [Reference Caputo and Vinatier4].
10 Proof of Theorem 1.7
Let F be any imaginary quadratic field such that
![]() $\operatorname {\mathrm {Cl}}(O_F)$
contains an element of order
$\operatorname {\mathrm {Cl}}(O_F)$
contains an element of order
![]() $4$
. In this section, we shall construct infinitely many counterexamples to Conjecture 1.4 by showing that if
$4$
. In this section, we shall construct infinitely many counterexamples to Conjecture 1.4 by showing that if
![]() $\ell $
is any sufficiently large prime with
$\ell $
is any sufficiently large prime with
![]() $\ell \equiv 3\ \pmod {4}$
and G is the generalized quaternion group
$\ell \equiv 3\ \pmod {4}$
and G is the generalized quaternion group
![]() $H_{4\ell }$
, then there are infinitely many tame G-extensions
$H_{4\ell }$
, then there are infinitely many tame G-extensions
![]() $F_{\pi }/F$
of fields such that
$F_{\pi }/F$
of fields such that
![]() $A_\pi $
exists and
$A_\pi $
exists and
![]() ${\mathcal J}^*_\infty (F_\pi /F) \neq 0$
. Hence, for these extensions,
${\mathcal J}^*_\infty (F_\pi /F) \neq 0$
. Hence, for these extensions,
![]() $(O_\pi ) \neq (A_\pi )$
in
$(O_\pi ) \neq (A_\pi )$
in
![]() $\operatorname {\mathrm {Cl}}({\mathbf Z} G)$
. This will prove Theorem 1.7.
$\operatorname {\mathrm {Cl}}({\mathbf Z} G)$
. This will prove Theorem 1.7.
In what follows, we fix an imaginary quadratic field F such that
![]() $\operatorname {\mathrm {Cl}}(O_F)$
contains an element of order
$\operatorname {\mathrm {Cl}}(O_F)$
contains an element of order
![]() $4$
. To prove Theorem 1.7, it will suffice to prove the following result, which we shall derive as a consequence of works of Fröhlich (see [Reference Fröhlich11]).
$4$
. To prove Theorem 1.7, it will suffice to prove the following result, which we shall derive as a consequence of works of Fröhlich (see [Reference Fröhlich11]).
Lemma 10.1 Suppose that
![]() $\ell $
is a sufficiently large prime and that
$\ell $
is a sufficiently large prime and that
![]() $G\simeq H_{4\ell }$
. Then there exists a G-extension
$G\simeq H_{4\ell }$
. Then there exists a G-extension
![]() $F_\pi /F$
of fields such that:
$F_\pi /F$
of fields such that:
-
(a)
 $F_\pi /F$
is ramified at only a single prime
$F_\pi /F$
is ramified at only a single prime
 ${\mathfrak p}$
of F with
${\mathfrak p}$
of F with
 ${\mathfrak p}\nmid \ell $
.
${\mathfrak p}\nmid \ell $
. -
(b) The prime
 ${\mathfrak p}$
does not split in
${\mathfrak p}$
does not split in
 $F_{\pi }/F$
.
$F_{\pi }/F$
. -
(c) The ramification index of
 ${\mathfrak p}$
is equal to
${\mathfrak p}$
is equal to
 $\ell $
.
$\ell $
.
Before we prove this result, we shall first show that Lemma 10.1 implies Theorem 1.7.
Proof of Theorem 1.7
First, we note that the decomposition subgroup of G at
![]() ${\mathfrak p}$
is equal to
${\mathfrak p}$
is equal to
![]() $H_{4\ell }$
. We also recall that for an odd prime
$H_{4\ell }$
. We also recall that for an odd prime
![]() $\ell $
, the generalized quaternion group
$\ell $
, the generalized quaternion group
![]() $H_{4\ell }$
has a single, irreducible, nontrivial symplectic character
$H_{4\ell }$
has a single, irreducible, nontrivial symplectic character
![]() $\chi $
, say.
$\chi $
, say.
If
![]() ${\mathfrak q}$
is unramified in
${\mathfrak q}$
is unramified in
![]() $F_\pi /F$
, then one has
$F_\pi /F$
, then one has
![]() $\operatorname {\mathrm {sgn}}(y(F_{\pi , {\mathfrak q}}/F_{{\mathfrak q}},\psi _{2}(\chi )))=1$
. On the other hand, Theorem 8.1 and Proposition 8.2 imply that
$\operatorname {\mathrm {sgn}}(y(F_{\pi , {\mathfrak q}}/F_{{\mathfrak q}},\psi _{2}(\chi )))=1$
. On the other hand, Theorem 8.1 and Proposition 8.2 imply that
In particular, if we now assume in addition that
![]() $\ell \equiv 3\ \pmod {4}$
, then it follows from [Reference Fröhlich14, Chapter II, Proposition 4.4] that the element
$\ell \equiv 3\ \pmod {4}$
, then it follows from [Reference Fröhlich14, Chapter II, Proposition 4.4] that the element
![]() ${\mathcal J}^*_\infty (F_\pi /F) \in \operatorname {\mathrm {Cl}}({\mathbf Z} G)$
(see Definitions 8.3 and 8.5 and Proposition 8.6) is nontrivial. (We remark in passing that if instead
${\mathcal J}^*_\infty (F_\pi /F) \in \operatorname {\mathrm {Cl}}({\mathbf Z} G)$
(see Definitions 8.3 and 8.5 and Proposition 8.6) is nontrivial. (We remark in passing that if instead
![]() $\ell \equiv 1\ \pmod {4}$
, then the same argument shows that
$\ell \equiv 1\ \pmod {4}$
, then the same argument shows that
![]() ${\mathcal J}^*_\infty (F_\pi /F) = 0$
.)
${\mathcal J}^*_\infty (F_\pi /F) = 0$
.)
The remainder of this section will be devoted to the construction of the extensions described in Lemma 10.1.
Let L be an unramified, cyclic extension of F of degree
![]() $4$
. We write
$4$
. We write
![]() $E/F$
for the quadratic subextension of
$E/F$
for the quadratic subextension of
![]() $L/F$
and write
$L/F$
and write
![]() $\varphi _{E/F}$
for the quadratic character of
$\varphi _{E/F}$
for the quadratic character of
![]() $E/F$
on ideals of F. We also view this as an idele class character of F. If
$E/F$
on ideals of F. We also view this as an idele class character of F. If
![]() $\omega $
denotes the idele class character of E that cuts out the extension
$\omega $
denotes the idele class character of E that cuts out the extension
![]() $L/E$
, then
$L/E$
, then
![]() $\omega $
is of quaternion type (i.e., the restriction of
$\omega $
is of quaternion type (i.e., the restriction of
![]() $\omega $
to
$\omega $
to
![]() $J(F)$
is equal to
$J(F)$
is equal to
![]() $\varphi _{E/F}$
—see [Reference Fröhlich11, p. 405].)
$\varphi _{E/F}$
—see [Reference Fröhlich11, p. 405].)
For each prime
![]() $\ell $
, the symbol
$\ell $
, the symbol
![]() $\eta _\ell $
will denote a primitive
$\eta _\ell $
will denote a primitive
![]() $\ell $
th root of unity. Then, following [Reference Fröhlich11, Theorem 4], we consider the following conditions on primes.
$\ell $
th root of unity. Then, following [Reference Fröhlich11, Theorem 4], we consider the following conditions on primes.
Property 10.2 Let
![]() $\ell $
be an odd prime such that:
$\ell $
be an odd prime such that:
-
(a)
 $[F(\eta _\ell ) : F]$
is even.
$[F(\eta _\ell ) : F]$
is even. -
(b)
 $E\not \subseteq F(\eta _\ell +\eta _\ell ^{-1})$
.
$E\not \subseteq F(\eta _\ell +\eta _\ell ^{-1})$
. -
(c) The class number of E is not divisible by
 $\ell $
.
$\ell $
.
We remark that these properties are satisfied for all sufficiently large
![]() $\ell $
. (We observe, in particular, that in our case, Property 10.2(b) is automatically satisfied for sufficiently large
$\ell $
. (We observe, in particular, that in our case, Property 10.2(b) is automatically satisfied for sufficiently large
![]() $\ell $
since
$\ell $
since
![]() $E/F$
is unramified.)
$E/F$
is unramified.)
Henceforth, we therefore fix a prime
![]() $\ell $
satisfying Property 10.2 and abbreviate
$\ell $
satisfying Property 10.2 and abbreviate
![]() $\eta _\ell $
to
$\eta _\ell $
to
![]() $\eta $
. We then write
$\eta $
. We then write
![]() $\Sigma _{-}$
for the set of primes
$\Sigma _{-}$
for the set of primes
![]() ${\mathfrak p}$
of F satisfying the following properties (see [Reference Fröhlich11, equation (8.5)]).
${\mathfrak p}$
of F satisfying the following properties (see [Reference Fröhlich11, equation (8.5)]).
Property 10.3 Let
![]() ${\mathfrak p}$
be a finite prime of F such that:
${\mathfrak p}$
be a finite prime of F such that:
-
(a) The prime
 ${\mathfrak p}$
is inert in
${\mathfrak p}$
is inert in
 $E/F$
(ie.
$E/F$
(ie.
 $\varphi _{E/F}({\mathfrak p}) = -1$
).
$\varphi _{E/F}({\mathfrak p}) = -1$
). -
(b)
 $N_{F/{\mathbf Q}} \equiv -1\ {\pmod \ell }$
.
$N_{F/{\mathbf Q}} \equiv -1\ {\pmod \ell }$
.
In what follows, if
![]() ${\mathfrak p} \in \Sigma _{-}$
, we write
${\mathfrak p} \in \Sigma _{-}$
, we write
![]() ${\mathfrak p}_{E}$
for the unique prime of E lying above
${\mathfrak p}_{E}$
for the unique prime of E lying above
![]() ${\mathfrak p}$
.
${\mathfrak p}$
.
Our argument relies on the following result of Fröhlich (see [Reference Fröhlich11, pp. 432–434]). We state the result and then describe an outline of the proof. We refer the reader to [Reference Fröhlich11] for complete details.
Theorem 10.4 There are infinitely many primes in
![]() $\Sigma _{-}$
(in fact, a subset of positive Chebotarev density) for which the following statement is true: there exists a nontrivial idele class character
$\Sigma _{-}$
(in fact, a subset of positive Chebotarev density) for which the following statement is true: there exists a nontrivial idele class character
![]() $\theta $
of E of order
$\theta $
of E of order
![]() $\ell $
, and of dihedral type (i.e., the restriction of
$\ell $
, and of dihedral type (i.e., the restriction of
![]() $\theta $
to
$\theta $
to
![]() $J(F)$
is trivial) which is ramified at
$J(F)$
is trivial) which is ramified at
![]() ${\mathfrak p}_{E}$
and which is unramified at all other finite places of E.
${\mathfrak p}_{E}$
and which is unramified at all other finite places of E.
Proof We remark that necessary conditions for such a
![]() $\theta $
to exist are given in [Reference Fröhlich11, Section 8, Lemma 5]. The existence of
$\theta $
to exist are given in [Reference Fröhlich11, Section 8, Lemma 5]. The existence of
![]() $\theta $
is demonstrated on pages 433 and 434 of loc. cit. via the following argument.
$\theta $
is demonstrated on pages 433 and 434 of loc. cit. via the following argument.
Recall that
![]() $\eta $
is a primitive
$\eta $
is a primitive
![]() $\ell $
th root of unity, and set
$\ell $
th root of unity, and set
(Note that this field is denoted by L in [Reference Fröhlich11, p. 433, l. 9], which is an unfortunate clash of notation with the field L defined earlier in loc. cit. (see [Reference Fröhlich11, p. 407]).
Write
![]() ${\widetilde {M}}$
for the extension of M obtained by adjoining the elements
${\widetilde {M}}$
for the extension of M obtained by adjoining the elements
It is shown in loc. cit. that for each prime
![]() ${\mathfrak p}$
of F satisfying the following Frobenius conditions, there exists an idele class character
${\mathfrak p}$
of F satisfying the following Frobenius conditions, there exists an idele class character
![]() $\theta $
of E satisfying the properties we seek.
$\theta $
of E satisfying the properties we seek.
Property 10.5 For every prime
![]() $\mathfrak {P}$
of
$\mathfrak {P}$
of
![]() $\widetilde {M}$
lying above
$\widetilde {M}$
lying above
![]() ${\mathfrak p}$
, the Frobenius element
${\mathfrak p}$
, the Frobenius element
![]() $\delta =(\mathfrak {P}, \widetilde {M}/F)$
satisfies:
$\delta =(\mathfrak {P}, \widetilde {M}/F)$
satisfies:
-
(F1)
 $\delta ^2=1$
.
$\delta ^2=1$
. -
(F2)
 $\delta |_{E}$
is nontrivial (so
$\delta |_{E}$
is nontrivial (so
 ${\mathfrak p}$
does not split in
${\mathfrak p}$
does not split in
 $E/F$
).
$E/F$
). -
(F3)
 $\delta \mid _{F(\eta )}$
is nontrivial (so
$\delta \mid _{F(\eta )}$
is nontrivial (so
 ${\mathfrak p}$
satisfies Property 10.3(b)).
${\mathfrak p}$
satisfies Property 10.3(b)).
The set of primes
![]() ${\mathfrak p}$
of F satisfying Property 10.5 has positive Chebotarev density, and all such primes lie in
${\mathfrak p}$
of F satisfying Property 10.5 has positive Chebotarev density, and all such primes lie in
![]() $\Sigma _{-}$
.
$\Sigma _{-}$
.
Let
![]() $\theta $
be an idele class character of E as constructed in Theorem 10.4, and let
$\theta $
be an idele class character of E as constructed in Theorem 10.4, and let
![]() $N/E$
denote the extension cut out by
$N/E$
denote the extension cut out by
![]() $\theta $
. Then
$\theta $
. Then
![]() $N/E$
is cyclic of order
$N/E$
is cyclic of order
![]() $\ell $
, ramified (necessarily totally) at
$\ell $
, ramified (necessarily totally) at
![]() ${\mathfrak p}_E$
, and at no other primes of E. As
${\mathfrak p}_E$
, and at no other primes of E. As
![]() $\theta $
is of dihedral type, the extension
$\theta $
is of dihedral type, the extension
![]() $N/F$
is dihedral of order
$N/F$
is dihedral of order
![]() $2\ell $
.
$2\ell $
.
Set
![]() $\psi := \omega \theta $
. Then
$\psi := \omega \theta $
. Then
![]() $\psi $
is an idele class character of E of quaternion type, and we deduce that
$\psi $
is an idele class character of E of quaternion type, and we deduce that
![]() $F_{\pi (\psi )}:= NL$
is an
$F_{\pi (\psi )}:= NL$
is an
![]() $H_{4\ell }$
extension of F. (Note that the field that we call
$H_{4\ell }$
extension of F. (Note that the field that we call
![]() $F_{\pi (\psi )}$
is denoted by the symbol
$F_{\pi (\psi )}$
is denoted by the symbol
![]() $F_\psi $
in [Reference Fröhlich11].) The extension
$F_\psi $
in [Reference Fröhlich11].) The extension
![]() $F_{\pi (\psi )}/F$
is ramified only at
$F_{\pi (\psi )}/F$
is ramified only at
![]() ${\mathfrak p}$
, with ramification index
${\mathfrak p}$
, with ramification index
![]() $\ell $
. We have the following diagram of fields and corresponding idele class characters (where we write
$\ell $
. We have the following diagram of fields and corresponding idele class characters (where we write
![]() ${\varphi }$
for
${\varphi }$
for
![]() ${\varphi }_{E/F}$
):
${\varphi }_{E/F}$
):

To complete the proof of Lemma 10.1, it suffices to show that in Theorem 10.4, there are infinitely many choices of
![]() ${\mathfrak p}$
(and so of
${\mathfrak p}$
(and so of
![]() $\theta $
) such that the decomposition group of
$\theta $
) such that the decomposition group of
![]() ${\mathfrak p}$
in
${\mathfrak p}$
in
![]() $F_{\pi (\psi )}/F$
is not abelian. This is equivalent to imposing an additional Frobenius condition on
$F_{\pi (\psi )}/F$
is not abelian. This is equivalent to imposing an additional Frobenius condition on
![]() ${\mathfrak p}$
. In order to do this, we require the following lemma.
${\mathfrak p}$
. In order to do this, we require the following lemma.
Lemma 10.6 The extensions
![]() $\widetilde {M}/E$
and
$\widetilde {M}/E$
and
![]() $L/E$
are linearly disjoint. Hence,
$L/E$
are linearly disjoint. Hence,
![]() $[{\widetilde {M}}L:{\widetilde {M}}] = 2$
.
$[{\widetilde {M}}L:{\widetilde {M}}] = 2$
.
Proof The extension
![]() $\widetilde {M}/E$
has a unique quadratic subextension, viz. the unique quadratic subextension of
$\widetilde {M}/E$
has a unique quadratic subextension, viz. the unique quadratic subextension of
![]() $M/E$
(recall that
$M/E$
(recall that
![]() $M = E(\eta )$
). This extension is ramified at places above
$M = E(\eta )$
). This extension is ramified at places above
![]() ${\mathfrak p}$
, and so cannot be equal to the unramified quadratic extension
${\mathfrak p}$
, and so cannot be equal to the unramified quadratic extension
![]() $L/E$
.
$L/E$
.
We now fix an element
![]() $\delta _1 \in \operatorname {\mathrm {Gal}}({\widetilde {M}}L/F)$
which maps under the obvious quotient map onto the element
$\delta _1 \in \operatorname {\mathrm {Gal}}({\widetilde {M}}L/F)$
which maps under the obvious quotient map onto the element
![]() $\delta \in \operatorname {\mathrm {Gal}}({\widetilde {M}}/F)$
constructed in the proof of Theorem 10.4 (see (10.5)), and we consider the set of primes
$\delta \in \operatorname {\mathrm {Gal}}({\widetilde {M}}/F)$
constructed in the proof of Theorem 10.4 (see (10.5)), and we consider the set of primes
![]() ${\mathfrak p}$
of F satisfying the following Frobenius condition.
${\mathfrak p}$
of F satisfying the following Frobenius condition.
Property 10.7 For every prime
![]() $\mathfrak {Q}$
of
$\mathfrak {Q}$
of
![]() $\widetilde {M}L$
lying above
$\widetilde {M}L$
lying above
![]() ${\mathfrak p}$
,
${\mathfrak p}$
,
-
(F4) the Frobenius element
 $(\mathfrak {Q}, \widetilde {M}L/F)$
lies in the conjugacy class of
$(\mathfrak {Q}, \widetilde {M}L/F)$
lies in the conjugacy class of
 $\delta _1$
.
$\delta _1$
.
The set of primes
![]() ${\mathfrak p}$
satisfying (10.7) has positive Chebotarev density, and plainly if
${\mathfrak p}$
satisfying (10.7) has positive Chebotarev density, and plainly if
![]() ${\mathfrak p}$
satisfies (10.7), then it also satisfies (10.5).
${\mathfrak p}$
satisfies (10.7), then it also satisfies (10.5).
Suppose that
![]() ${\mathfrak p}$
satisfies (10.7). Then the corresponding extension
${\mathfrak p}$
satisfies (10.7). Then the corresponding extension
![]() $F_{\pi (\psi )}/F$
constructed above is an
$F_{\pi (\psi )}/F$
constructed above is an
![]() $H_{4\ell }$
-extension unramified outside
$H_{4\ell }$
-extension unramified outside
![]() ${\mathfrak p}$
, in which
${\mathfrak p}$
, in which
![]() ${\mathfrak p}$
is nonsplit and ramified, with ramification index
${\mathfrak p}$
is nonsplit and ramified, with ramification index
![]() $\ell $
. Hence,
$\ell $
. Hence,
![]() $F_{\pi (\psi )}/F$
an extension satisfying the conditions of Lemma 10.1.
$F_{\pi (\psi )}/F$
an extension satisfying the conditions of Lemma 10.1.
This completes the proof of Lemma 10.1.
Remark 10.8 It is shown in [Reference Fröhlich11, Theorem 4] that for the extensions
![]() $F_{\pi (\psi )}/F$
constructed above satisfying the conditions of Lemma 10.1, we have
$F_{\pi (\psi )}/F$
constructed above satisfying the conditions of Lemma 10.1, we have
This implies that
![]() $(O_{\pi (\psi )})\neq 0$
(see (1.1)), and so, since
$(O_{\pi (\psi )})\neq 0$
(see (1.1)), and so, since
![]() ${\mathcal J}^*_\infty (F_{\pi (\psi )}/F) \neq 0$
, it follows from Theorem 1.5 that
${\mathcal J}^*_\infty (F_{\pi (\psi )}/F) \neq 0$
, it follows from Theorem 1.5 that
![]() $(A_{\pi (\psi )}) = 0$
.
$(A_{\pi (\psi )}) = 0$
.
Remark 10.9 Dominik Bullach has explained to us how explicit counterexamples to Conjecture 1.4 can also be derived from Theorem 1.5 by using general results of Neukirch on the embedding problem (see [Reference Neukirch21]) rather than the explicit computations of Fröhlich in [Reference Fröhlich11].
Acknowledgments
The first author learned of the work of [Reference Caputo and Vinatier4] and of the conjecture of Erez from conversations with Philippe Cassou-Noguès and Boas Erez. He is extremely grateful to them, as well as to Werner Bley and Cindy Tsang, for their subsequent interest in this project. We are also very grateful to Dominik Bullach for additional insight into the manner in which counterexamples to Conjecture 1.4 can be derived from Theorem 1.5 (see Remark 10.9).